Chap8 Tree-Based Methods

서지은·2021년 11월 19일
ISLR

ISLR

목록 보기
6/6
post-thumbnail

8.1 The Basics of Decision Trees

8.1.1 Regression Trees

<Predicting Baseball Player's Salaries Using Regression Trees>

  • predictors : Years(메이저리그에서 몇년있었는지) / Hits(전년도의 Hits수)

  • reponse : Salary

  • Tree 구조 : Nodes(Terminal Nodes, Internal Nodes) / Splitting Ruels / branches

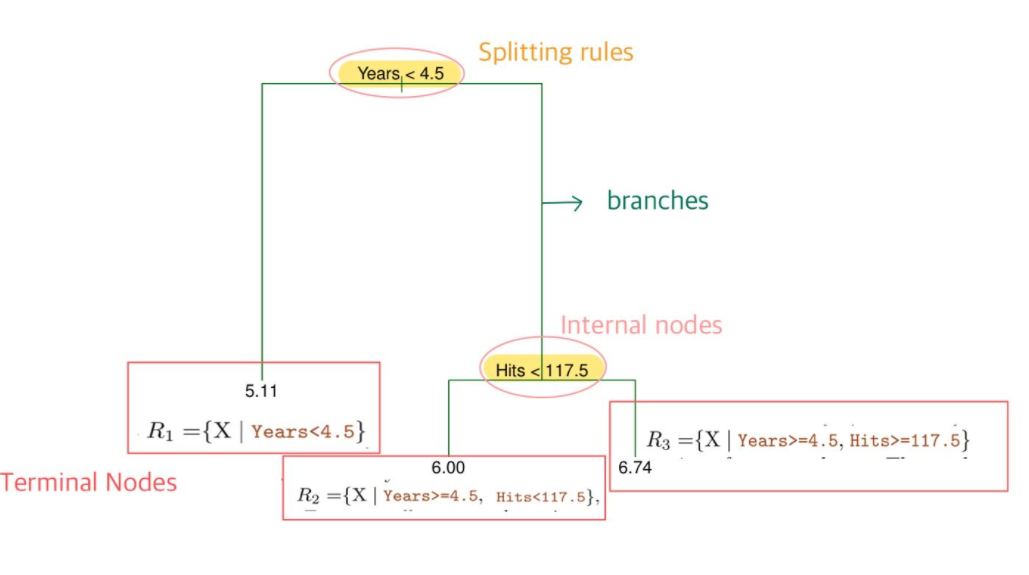
Terminal Nodes 를 수식으로 표현하면 위와 같이 R1,R2,R3의 Region으로 표현할 수 있음

<Predicting Baseball Player's Salaries Using Regression Trees>

  • Splitting Rules에 따라 데이터를 나누고
    → 최종 분리된 이후 예측값은 각 Ternimal Node (최종으로 분류되어 나온 Region)에 해당하는 mean response value for the training observations 로 함

(따라서, 같은 terminal Nodes에 있는 data들의 예측값으 모두 동일)

  • 그럼 어떻게 Regions R1,R2,R3..Rj (Terminal Nodes, Tree 구조) 를 결정하는가?

goal : find boxes R1,R2,R3..Rj that minimize the RSS

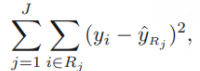
  • Recursive binary Splitting

모든 경우의 수의 Splitting case를 전부 살펴볼 수 없기 때문에 top-down approach를 이용한다.

  1. RSS를 가장 작게하는 Predictor 와 적당한 Cutpoint를 지정하여 Splitting Rule을 만든다

HOW? 모든 Predictors와 그에 해당하는 모든 cutpoint를 고려한 뒤, lowest RSS를 가져다주도록 Splitting Rule을 결정

  1. 위와 같은 방법을 반복하여 , stopping criteria에 도달할 때까지 Split한다.

단. 전 단계에서 생성된 2개의 regions을 전부 split하는 것이 아닌, 두개 중 하나의 region만 Split한다.

Tree Pruning

  • Tree가 너무 복잡해지면 Overfitting이 일어날 수 있음
  • Smaller Tree (with fewer splits)은 lower variance 와 Better interpretation을 제공하지만, bias는 커진다.

적절한 tree structure는 어떻게 얻어내는가?

  • 적절한 기준점(thresold)에 다다르면 tree split을 stop하는 방법론을 사용하여 ,적절하게 tree의 split 개수를 조정할 수 있음. (최소 RSS에 다다르지 않더라도)

→ 그러나 이렇게 단순한 방법으로 tree structure를 결정하면, 중요한 split rule이 뒤에 나오게 될 경우 RSS가 매우 커지는 단점이 있음.

  • Tree Pruning : Tree의 Complexity는 낮추면서 동시에 RSS를 작게하기 위해 사용하는 방법
  1. Very Large Tree T0를 설정
  2. 적절한 Subtree (Test Error rate을 가장 작게 하는 → 이때 Test Error rate은 CV(Cross validation)을 이용하여 계산) 를 얻기 위해 prune it back(가지치기)

하지만 모든 subtree의 test error rate을 전부 계산할 수는 없음

→ selecting a samll set of subtrees for consideration : Cost Complexity pruning

  • Cost Complexity pruning

: 모든 subtree를 계산하는 것이 아니라, 적절한 tuning parameter에 따라 결정된 subtree 후보 몇개만 살펴 보는 것

T : # of terminal tree (tree complexity)

a : tuning parameter

좌측 항 : RSS / 우측 항 : tree complexity에 대한 Penalty (a)

(a = 0이면, RSS를 최소로 하는 tree를 결정하면 되니까, T0를 선택하게 됨.

a 가 커질수록, Tree complexity에 대한 penalty는 커짐)

  1. CV를 이용해 test error rate이 가장 작아질 때의 a 값을 결정함 (tree complexity에 대한 penalty를 얼마나 줄 것인지 결정)
  2. a가 정해지면 그때 해당하는 subtree들을 이용하여 test error rate을 cv를 이용해 계산한 뒤 그 값이 가장 작아지는 tree를 선택함.
  • Cost Complexity pruning 를 이용한 Tree stucture결정 알고리즘

1 : 가장 큰 Tree를 만드는 것 (각 terminal node에 포함된 observations의 수가 some min number보다 작을 때)
2, 3 : pruning parameter값 결정
4 : final tree결정

8.1.2 Classifcation Trees

  • 예측값 : 해당 Terminal Node에서 가장 빈도수가 높은 class of training observations 로 예측

    (Most Commly occurring class)

  • RSS 대신 Classification error rate을 이용

<Classification error rate>

Most commonly occurring class (해당 Terminal Node에서 예측할 Class)에 속하지 못한 class의 비율


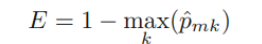
(Pmk : m번째 구역의 k번째 class의 비율)

tree-growing에 sensitive하지 않기 때문에, 뒤에 두개의 방법을 더 선호함

<Gini index (Gini impurity)>


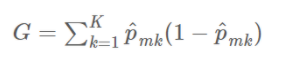
class가 덜 분류되어 덜 순수한 정도 반영

ex ) Class 가 2개 있는 경우 Pm1 = 1 , Pm2 =0 이어서 완벽히 분리된 경우 G는 0으로 계산된다.

Pm1 = 1/2 , Pm2 =1/2 이어서 반반 섞여 있는 경우, G는 0.5로 계산되어 값이 커지는 것을 알 수 있다.

→ Mth node가 pure(잘 분리되어 있을수록) small value를 가진다.

<Entropy>


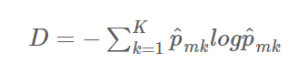
Gini index 와 거의 유사한 값을 가진다

분류 트리를 생성할 때는 gini impurity 혹은 entropy가 분기를 나누는 데에는 더 적합하여 주로 사용된다. 반면, 트리를 pruning 하는 작업에서는 정확도를 높이기 위해 classification error rate가 더 선호된다.

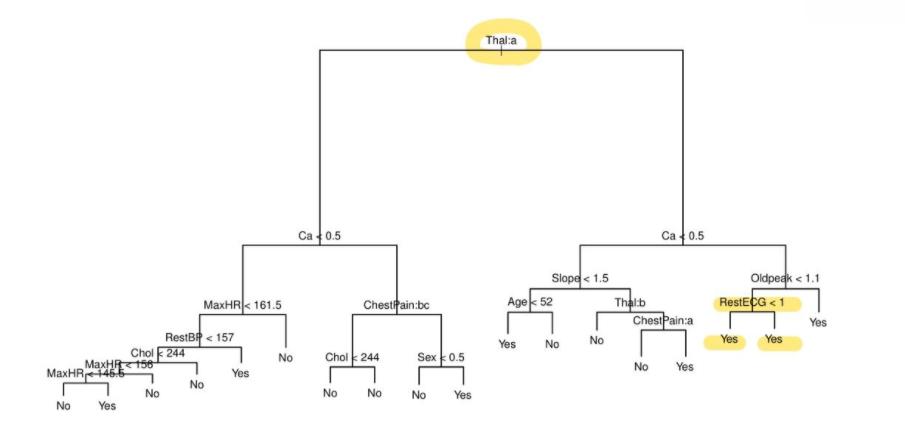
  • tree model : predictors가 qualitative일 때도 사용가능
  • Split했는데도 같은 predicted value를 줄 수 있음 → 그럼 왜 split하는가? node purity를 위해

한쪽 leaf이 보다 정확히 class를 분류하여 node purity를 증가시키는 경우 → test 에서의 정확한 분리를 위하여

8.1.3 Tree Versus Linear Models

linear model : features와 response의 관계가 linear일 때

tree model : non-linear and complex relationship btw features and response / 해석 및 시각화의 용이성이 필요할 때

8.1.4 Advantages and Disadvantages of Trees

Advantages

  1. explain하기 쉽다 (해석의 용이성)
  2. 사람의 decision rule과 비슷
  3. 시각화 하기 쉬움
  4. dummies 생성없이 범주형 변수 다루기 쉬움

Disdvantages

  1. same level of predictive accuracy 를 가지지 않음
  2. non-robust : data의 작은 변화에 크게 반응함

: High Variance

→ 문제 해결 : aggregating many decision trees

8.2 Bagging, Random Forests, Boosting, and Bayesian Additive Regression Tree

ensemble : simple building block model을 combining

8.2.1 Bagging

goal : Low varaince → averaging a set of observations reduce variance

여러개의 seperate training set을 이용해 얻어낸 값을 평균 내면 variance가 낮아짐

실제로는 train set을 여러개 얻기 어렵기 때문에

  1. Boostrap(Chap5)방법을 이용하여 bootstrapped training data sets을 얻고
  2. 각 training set에서 얻어진 predcitions을 평균낸다


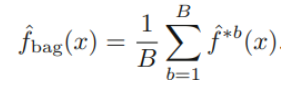
→ Bagging

tree에서 Bagging

  1. 각 tree B 는 deep and not pruned → high variance & low biase
  2. Averaging these B trees → reduce variance

B의 개수(single tree의 개수)는 overfitting 일으키지 않음

Out-of-Bag Error Estimaion

  • 추출 되지 않아 (Boostrap되지 않아) training에 사용되지 않은 데이터 : Out-of-bag(OOB)

→ 이를 이용하여 Validation Test

  1. 전체 데이터 중 약 2/3정도가 한번의 Bootstarp에서 추출됨

  2. B개의 single tree 중 i 번째 observation을 사용하지 않은 B/3개의 tree를 앙상블 하여 i번째 Observation에 대한 Validation Test 를 진행함

  3. 총 n개의 obervaion에 대해서 위와 같은 방법으로 prediction하면, overall OOB MSE / classification error를 얻을 수 있음

  • cross-validation이 더욱 정확한 test error추정을 가능하게 하지만, 데이터가 충분히 많고 충분히 많은 B번의 Bootstrap의 경우 OOB 역시 비슷한 성능을 냄

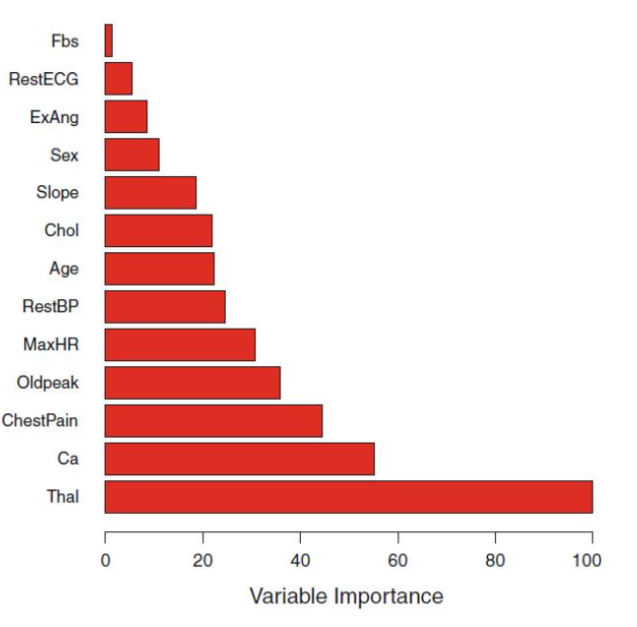
Variable Importance Measures

Bagging을 사용하면 model을 interpret하기 어려워지고, 어떤 variables가 tree building에 중요한 역할을 했는지 판별하기어려워짐

→ 이때, 각 tree에서 어떤 variables가 RSS 혹은 Gini Index를 줄이는데 일조했는지 record하고 가장 기여도가 높았던 순서대로 제시해줌으로써, Variable Importance 를 측정할 수 있게 해줌

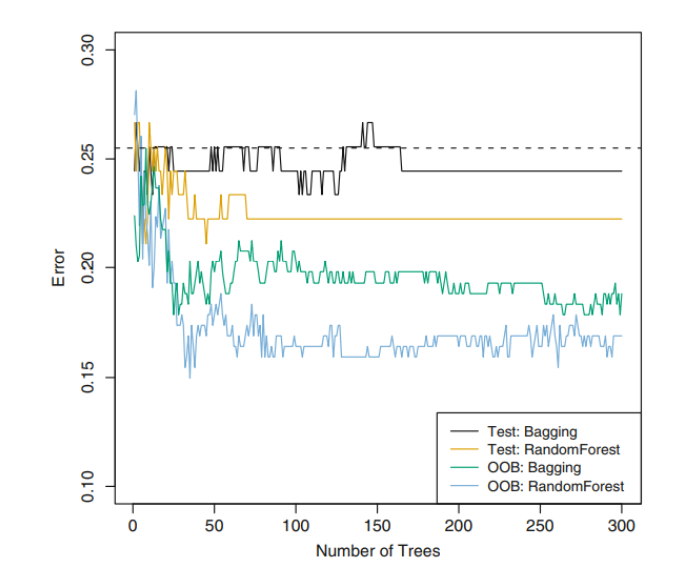
8.2.2 Random Forests

Bagging을 이용한다고 해도, 중요한 변수들은 고정되어있어 각 tree의 구조는 유사할 것이다

→ highly correlated trees

→ highly correlated quantites 들을 평균내는 것은 reduction Variance에 큰 도움이 안 됨

→ uncorrelated trees들이 필요 :

  • 각 tree를 구성할 때, 전체 predictors 이용 대신 m개의 predictors만 고려하여 tree 구성.
  • 각각의 tree는 m개의 변수만을 이용하게 되는데, 이때 변수의 importance를 고려해 m개를 고르는 것이 아니라, 단순하게 일부 개수의 변수만 사용함

그렇게 선택된 m개의 변수로 각 tree 구성 후, 평균을 내어 최종 예측 model이 구성됨

( m 의 개수는 일반적으로 p의 제곱근 : 그때 가장 성능 좋음)

8.2.3 Boosting

Bagging과 유사하나, bootstrap sampling을 이용하지 않고 이전 tree 정보를 이용하여 sequentially grown 함.

  1. Decision tree를 이전 model의 Residual에 fit : residual에 fit하기 때문에 small tree (d가 작음)
  2. Fitted function에 residual에 대한 정보를 update하기 위하여 1번에서 fit한 model의 결과를 더한다.
  3. residual을 update한다.

→ repeat하여 Fitted function 을 improving

: each tree depends strongly on the trees that have already been grown

Tuning Parameters

  1. The number of Trees : B
  • Bagging , Random Forest와 다르게 B가 커지면 Overfitting됨
  • B의 개수를 결정하기 위해서 CV사용
  1. shrinkaged parameter(lambda) : control the rate at which boosting learns
  • 0.01 , 0.001
  • B가 커지면 이 값이 작아져야 함
  1. The number d of splits in each tree : controls the complexity of the boosted ensemble
  • d=1일 때 works well (stump)

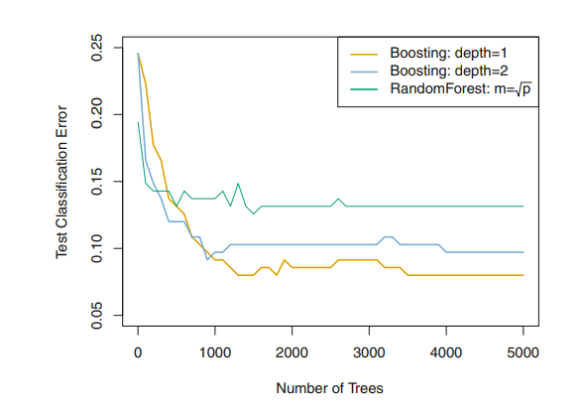
8.2.5 Summary of Tree Ensemble Methods

Bagging

  • 독립적으로 tree가 생성됨 따라서 각 tree는 모두 비슷

Random Forest

  • bagging과 유사 but 모든 single tree가 유사해지는 것을 방지하기 위하여 각 single tree마다 random하게 predictors를 선택하여 tree를 생성함

Boosting

  • Original data만 사용하고, random sample은 사용하지 않음
  • 연속적으로 tree 생성 → slow learning approach

: current model이 설명해내지 못한 signal(residual)을 이용해 tree를 fit하고 이를 이용하여 fitted function을 update 시키고, 설명되지 않은 residual에서 설명된 부분 또한 update시킴

profile
서지은
Data Analyst | Statistics
이전 포스트

Chap7

0개의 댓글