211007 CodeStates 54일차

오늘은 어제에 이어서 알고리즘을 하루 더 공부했다.
수학의 개념을 배우고 알고리즘 문제에 적용하는 방법을 배웠다.
기본적인 순열,조합,최대공약수,최소공배수의 개념과 그것을 구현하는 코드를 작성해보고, 페어분과 함께 수학적 개념을 이용하여 문제를 풀었다.

순열과 조합

순열은 뽑는 순서에 의미를 두고 n개 중에서 r개를 뽑는 연산이다.
조합은 뽑는 순서에 의미를 두지않고 n개 중에서 r개를 뽑는 연산이다.
순열과 조합 모두 n개 중에서 r개를 뽑는 연산이지만, 뽑는 순서에 의미를 두느냐의 여부가 둘의 차이점이다.

예를들어 [1,2,3,4]와 같이 4개의 원소를 갖는 배열에서 2개를 뽑는 가짓수를 계산할때, 순서에 의미를 두고 뽑는다면 가짓수는 다음과 같다.
$[1,2], [1,3], [1,4], [2,1], [2,3], [2,4],$
$[3,1], [3,2], [3,4], [4,1], [4,2], [4,3]$
=> 총 12가지 가짓수

순열은 뽑는 순서에 의미를 두기 때문에 $[1,2]$의 가짓수는 1을 먼저 뽑고 두번째로 2를 뽑는 경우이고, $[2,1]$은 2를 먼저 뽑고 두번째로 1을 뽑는 경우이기 때문에 엄연히 다른 경우이다.

조합은 순서에 의미를 두지 않으므로 $[1,2]$와 $[2,1]$은 같은 1가지의 경우이다.
순서에 의미를 두지않고 뽑는 조합의 가짓수는 다음과 같다.
$[1,2], [1,3], [1,4], [2,3], [2,4], [3,4]$
=> 총 6가지 가짓수

순열과 조합을 구하는 코드는 재귀를 이용하여 작성했다.

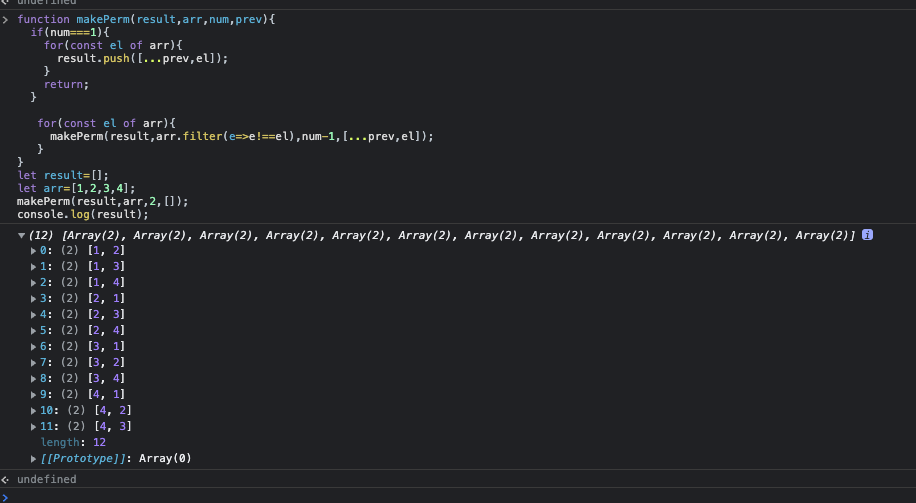
순열의 모든 경우의 수를 구하는 코드

function makePerm(result,arr,num,prev){
  // base 재귀함수가 종료될 조건
  if(num===1){
    for(const el of arr){
      result.push([...prev,el]);
    }
    return;
  }
  // recursive 재귀함수를 호출
   for(const el of arr){
     makePerm(result,arr.filter(e=>e!==el),num-1,[...prev,el]);
   }
}
let result=[];
let arr=[1,2,3,4];
makePerm(result,arr,2,[]);
console.log(makePerm);

result: 모든 경우의 수를 저장할 배열
arr: 뽑을 수 있는 원소들을 담은 배열
num: 뽑아야 하는 갯수
prev: 이전까지 뽑았던 원소들을 저장하는 배열

뽑아야 하는 갯수를 하나씩 줄여가며 이전까지 선택했던 원소들에 arr의 원소를 하나씩 추가하며 재귀함수를 호출했다.
모든 경우의 수만큼 prev가 복사되어 result에 push된다.

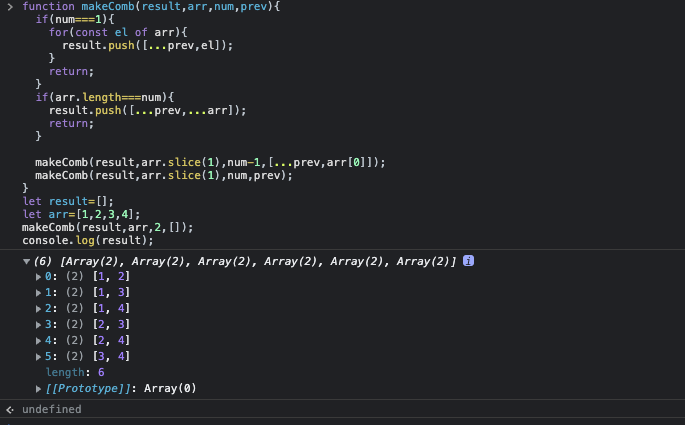
조합의 모든 경우의 수를 구하는 코드

function makeComb(result,arr,num,prev){
  // base 재귀함수가 종료될 조건
  if(num===1){
    for(const el of arr){
      result.push([...prev,el]);
    }
    return;
  }
  if(arr.length===num){
    result.push([...prev,...arr]);
    return;
  }
  
  // recursive  재귀함수를 호출
  // 첫번째요소를 선택하는경우
  makeComb(result,arr.slice(1),num-1,[...prev,arr[0]]);
  // 첫번째요소를 선택하지 않는경우
  makeComb(result,arr.slice(1),num,prev);
}
let result=[];
let arr=[1,2,3,4];
makeComb(result,arr,2,[]);
console.log(result);

result: 모든 경우의 수를 저장할 배열
arr: 뽑을 수 있는 원소들을 담은 배열
num: 뽑아야 하는 갯수
prev: 이전까지 뽑았던 원소들을 저장하는 배열
인자는 이전의 순열을 구하는 함수와 같다.

순열을 구하는 함수와 다른점은 조합은 순서에 의미를 두지 않고 뽑으므로 재귀함수를 두 가지 경우로 나누어 호출했다.
(arr의 첫번째 요소를 뽑는 경우와 arr의 첫번째 요소를 뽑지 않는경우)
arr의 첫번째 요소를 뽑는 경우에는 prev에 요소를 추가하고 뽑아야하는 갯수를 1을 차감해야한다.
arr의 첫번째 요소를 뽑는 경우에는 prev에 요소를 추가하지 않고 뽑아야하는 갯수도 그대로 재귀함수에 전달해야한다.
또한 재귀함수가 종료될 조건도 한가지가 추가되었다.
base의 두번째 if절인데, 순열의 경우에는 뽑아야 하는 갯수와 뽑을 수 있는 원소의 수가 같아도 여러가지 경우의 수가 가능하다.
$[1,2]$중에 2개를 뽑아야할때, 순서에 의미를 둔다면 $[1,2]$와 $[2,1]$은 다른 경우이기 때문이다.
다만 조합은 순서에 의미를 두지 않기 때문에 뽑아야하는 갯수와 뽑을 수 있는 원소의 수가 같다면 경우의 수는 한가지 밖에없다.
이는 이항계수의 성질 $_nC_n=1$의 의미와 같다.

최대공약수와 최소공배수

약수는 어떤수를 나누어 떨어지게 하는 수이고 배수는 어떤수에 정수를 곱하여 얻는 수이다.
8의 약수 => 8을 나누어 떨어지게 하는 수 1,2,4,8
9의 배수 => 9에 정수를 곱하여 얻는 수 9,18,27,36,..... (배수는 무한히 많다.)

공약수는 둘 이상의 수들이 공통으로 갖는 약수이며 최대공약수는 공약수들 중 가장 큰 수이다.
공배수는 둘 이상의 수들이 공통으로 갖는 배수이며 최소공배수는 공배수들 중 가장 작은 수이다.

우리는 중학교 수학을 배우면서 최대공약수와 최소공배수는 소인수분해를 통해 얻어지는 소인수들을 이용하여 구할 수 있다고 배웠다.
소인수분해는 어떤 수를 소수들의 곱으로 나타내는 것이다.

24,60의 최대공약수, 최소공배수 구하기

소인수분해를 코드로 작성하려면 일단 소수들을 찾아야하고 찾은 소수들을 이용해 두 숫자를 전부다 나누어 봐야한다.
컴퓨터의 연산속도가 빠르기는 하지만 숫자가 커진다면 소수들을 찾아야하는 범위가 넓어질 것이고 연산에 걸리는 시간도 오래걸릴 것이다.

유클리드 호제법

유클리드 호제법이란 최대공약수를 찾는 알고리즘으로 두 수 a,b(a>b)가 있다면 a와 b의 최대공약수는 b와 a를 b로 나눈 나머지 r의 최대공약수와 같다는 성질을 이용하여 나머지가 0이 될때 나누는 수가 최대공약수가 된다는 알고리즘이다.

유클리드 호제법을 이용해 78696과 19332의 최대공약수 구하기
$78696=19332*4+1368$
$19332=1368*14+180$
$1368=180*7+108$
$180=108*1+72$
$108=72*1+36$
$72=36*2+0$
=>78696과 19332의 최대공약수는 36이다.

이는 코드로 굉장히 간단하게 구현할 수 있다.

function findgcd(num1,num2){
  let arr=[Math.max(num1,num2),Math.min(num1,num2)];
  while(arr[1]!==0){
    arr.push(arr[0]%arr[1]);
    arr.shift();
  }
  return arr[0];
}

유클리드 호제법을 이용하여 간단한 코드로 최대공약수를 구할 수 있다.
하지만 최소공배수를 구하려면 어떻게 해야할까?
"두수의 곱은 두수의 최대공약수와 최소공배수를 곱한값과 같다."는 성질을 이용해 두수의 곱을 최대공약수로 나눠주면 최소공배수를 구할 수 있다.

function findlcm(num1,num2){
  let gcd=findgcd(num1,num2);
  return (num1*num2/gcd);
}