백준 1068번: 트리

문제: https://www.acmicpc.net/problem/1068

문제 풀이

트리 + BFS

주어지는 트리의 루트를 그래프 시작점으로 잡고 BFS를 진행함

제거되는 노드는 미리 방문처리를 해서 탐색하지 않게 함

현재 확인하는 노드에서 탐색 가능한 노드가 없으면 단말 노드이므로 정답에 1을 더함

탐색 가능한 모든 노드를 탐색해 단말 노드인지 확인하면 된다

풀이 설명

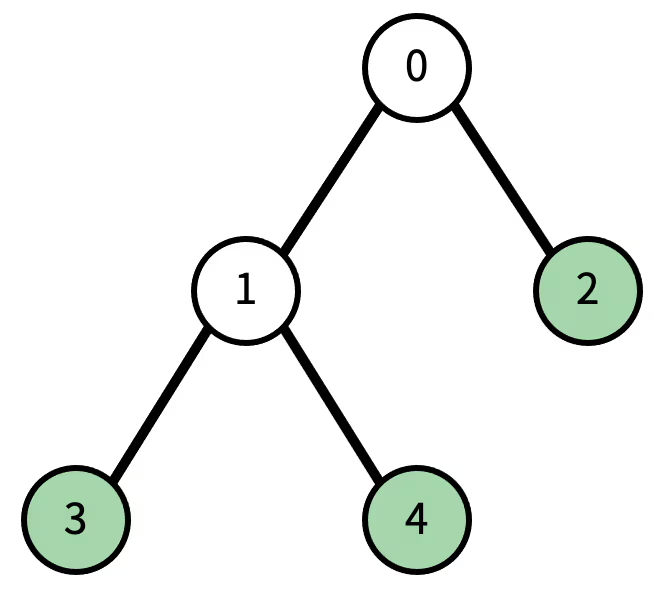
트리를 부모 노드에서 자식 노드로만 갈 수 있는 방향 그래프라고 생각해보자

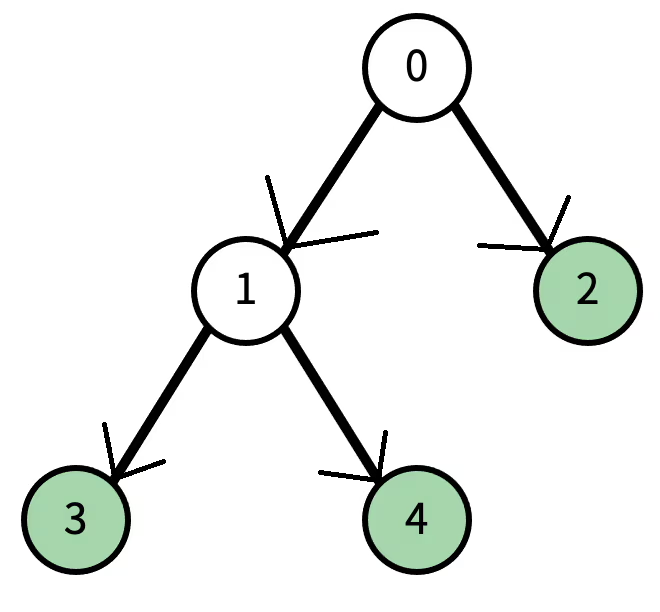
예시와 같이 왼쪽 그림과 같은 트리가 있으면 오른쪽 그림처럼 방향 그래프로 나타낼 수 있다

단말 노드는 자식이 없는 노드이고 우리가 방향 그래프를 부모 노드에서 자식 노드로 가는 방향 그래프라고 했기 때문에 그래프 탐색을 할 때 자식 노드가 존재하지 않아 더 이상 탐색할 수 없는 노드가 단말 노드가 된다

이 때 부모 노드에서 자식 노드로만 이동할 수 있기 때문에 트리 전체를 탐색하려면 루트 노드부터 탐색을 시작해야 한다

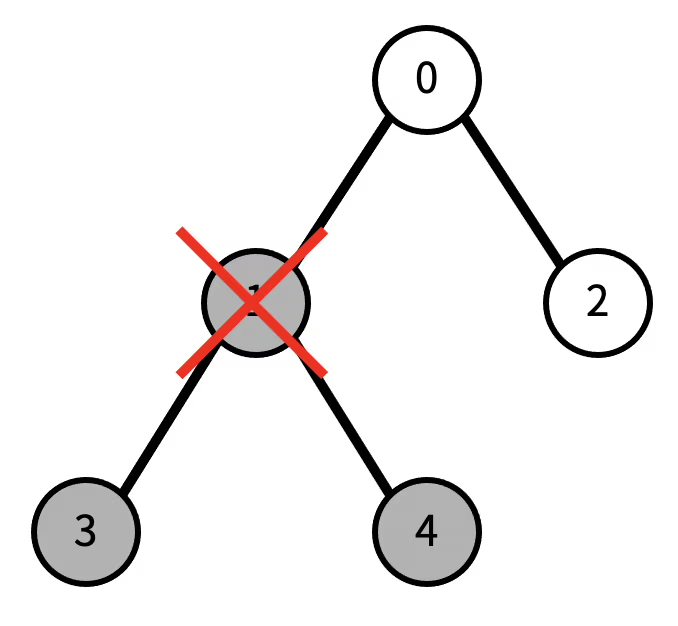
문제의 조건과 같이 노드 하나를 제거해 그 노드와 모든 자손이 트리에서 제거되는 것을 그래프 탐색으로 생각해보자

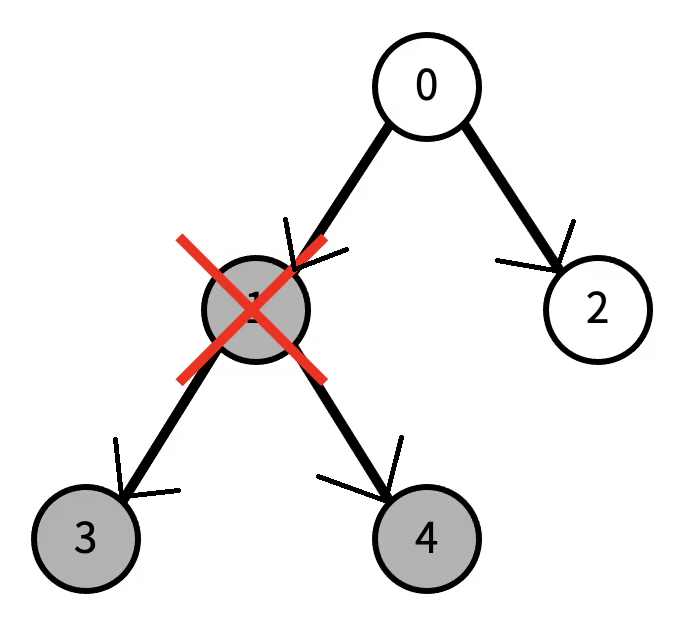
제거하려는 노드를 탐색하지 않으면 자연스럽게 그 모든 자손도 탐색하지 않게 된다, 따라서 제거하는 노드를 미리 방문처리 해놓으면 해당 노드와 모든 자손 노드들을 탐색하지 않는다

따라서 루트 노드에서부터 이미 방문된 노드를 제외하고 모든 노드를 탐색해 더이상 탐색할 경로가 없는 단말 노드를 찾으면 되는데, 탐색할 때 경로 자체보다는 현재 노드에서 탐색 가능한 노드의 수가 중요하기 때문에 DFS 보다는 BFS가 더 적합한 탐색 방법이다

소스 코드

import java.io.*
import java.util.*
import kotlin.collections.ArrayDeque

fun main(){
    val br = BufferedReader(InputStreamReader(System.`in`))
    val N = br.readLine().toInt()
    val st = StringTokenizer(br.readLine())
    var start = 0
    val graph = arrayListOf<ArrayList<Int>>()
    var answer = 0
    val visit = BooleanArray(N){false}
    visit[br.readLine().toInt()] = true
    for(i in 0 until N){
        graph.add(arrayListOf())
    }
    for(i in 0 until N){
        val j = st.nextToken().toInt()
        if(j == -1){
            start = i
        } else {
            graph[j].add(i)
        }
    }
    val queue = ArrayDeque<Int>()
    queue.add(start)
    while(queue.isNotEmpty()){
        val i = queue.removeFirst()
        if(visit[i]) continue
        var count = 0
        for(j in graph[i]){
            if(visit[j]) continue
            else{
                count++
                queue.add(j)
            }
        }
        if(count == 0){
            answer++
        }
    }
    println(answer)
}