백준 1074번: Z

문제: https://www.acmicpc.net/problem/1074

$2^n \times 2^n$인 2차원 배열이 주어지고 그 배열을 왼쪽 위, 오른쪽 위, 왼쪽 아래, 오른쪽 아래로 나눠서 순서대로 방문하기 때문에 배열을 계속 4등분 한다는 생각이 들었다.

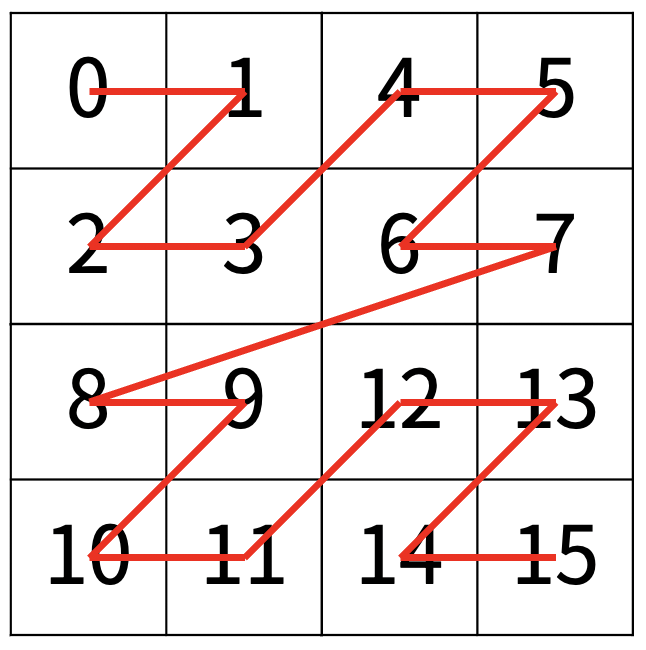
첫 번째 테스트 케이스를 예를 들어 위와 같은 $2^2 \times 2^2$ 배열이 있을 때 r이 3, c가 1이면 11이 적혀있는 칸을 가리키고, 이 배열을 4등분하면 해당 칸이 왼쪽 아래 배열에 위치하게 된다.

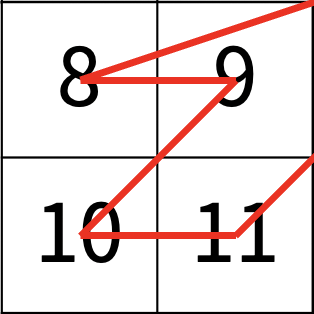
그렇게 4등분한 왼쪽 아래 배열을 보면 위의 그림과 같게 되고, 이미 왼쪽 위, 오른쪽 위의 순서가 지났기 때문에 4등분한 배열의 크기와 지난 순서의 곱인 $4 \times 2 = 8$부터 시작한다는 점을 알 수 있다. 그리고 11이 적혀있는 칸의 r이 원래 값에서 4등분한 배열의 행의 크기만큼 감소한 $3 - 2 = 1$이 되었다는 점을 알 수 있다. 그리고 이 칸이 현재 배열에서 오른쪽 아래에 있기 때문에 현재 배열의 4등분한 배열의 크기와 지난 순서 개수의 곱이 $1 \times 3 = 3$이 되고, 이 값에 앞서 구한 8을 더하면 답인 11이 나오게 된다.

따라서 문제를 해결하기 위해 한 칸만 남을때까지 배열을 4등분하면 답을 구할 수 있고 이를 재귀 함수로 정의할 수 있다.

static int Z(int N, int r, int c){
        if(N == 0){ // 마지막 한칸
            return 0;
        } else {
            int mid = (int) Math.pow(2, N-1); // 현재 칸이 배열의 어느 위치에 있는지 구분하기 위한 배열의 중간값
            int quarter = mid * mid; // 4등분한 배열의 크기
            if(r < mid){ // r이 mid보다 작다면 배열의 위쪽
                if(c < mid){ // c가 mid보다 작다면 배열의 왼쪽
                    return Z(N-1, r, c); //왼쪽 위
                } else {
                    return quarter + Z(N-1, r, c - mid); // 오른쪽 위
                }
            } else {
                if(c < mid){
                    return quarter * 2 + Z(N-1, r - mid, c); //왼쪽 아래
                } else {
                    return quarter * 3 + Z(N-1, r - mid, c - mid); // 오른쪽 아래
                }
            }
        }
    }

앞서 살펴본 점을 따라 작성한 재귀 함수다. 이 함수를 통해 첫 번째 테스트 케이스를 다시 본다면
N = 2, r = 3, c = 1인 상태로 함수에 진입하게 된다. 이때 mid값이 $2^{2-1} = 2$가 되어서 r과 c값을 살펴봤을 때 배열의 왼쪽 아래라는 것을 알 수 있다. 그리고 4등분한 배열의 크기가 $2 \times 2 = 4$이기 때문에 $4 \times 2 = 8$의 값을 현재 배열에서 구하고, N값을 줄이고, r이 줄인 배열에서의 칸과 맞게하기 위해 mid 값을 빼서 함수를 다시 호출하게 된다.

다음으로 N = 1, r = 1, c = 1인 상태로 함수에 진입하게 되고, 이때 mid값이 $2^{1-1} = 1$, quarter값이 4등분한 배열의 크기인 $1 \times 1 = 1$이 된다. 이때 r과 c값을 확인하면 오른쪽 아래기 때문에 $1 \times 3 = 3$의 값을 구하고 다시 4등분한 배열에 맞게 값을 조절하고 함수를 호출한다.

마지막으로 N = 0, r = 0, c = 0인 상태로 함수에 진입하고, 이 때 더이상 배열을 나눌수 없기 때문에 0을 반환한다. 최종적으로 결과값은 $(4 \times 2) + (1 \times 3) + 0 = 11$이 되고 정답을 구할 수 있게 된다.