백준 14567번: 선수과목 (Prerequisite)

문제: https://www.acmicpc.net/problem/14567

문제 풀이

위상 정렬 + BFS

선수 과목 조건을 방향 그래프 형태로 저장, 이 때 그래프의 진입 차수를 prerequisite 배열에 저장

큐에 선수 과목이 없는 과목을 현재 학기와 함께 삽입

큐에서 꺼낸 과목이 선수 과목이 없으면 답을 저장하는 배열에 현재 학기를 저장

그래프 탐색을 통해 다음 과목을 확인해 현재 과목을 들으면 들을 수 있으면 큐에 삽입

큐가 빌 때까지 확인하고 정답 배열 출력

풀이 설명

문제에 조건에 따라 선수 과목 관계를 방향 그래프로 나타낼 수 있음

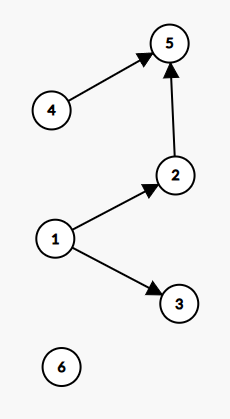
예제 2번을 그림과 같이 그래프로 나타낸다고 하면 선수 과목의 갯수가 그래프의 진입 차수가 되는 것을 알 수 있음

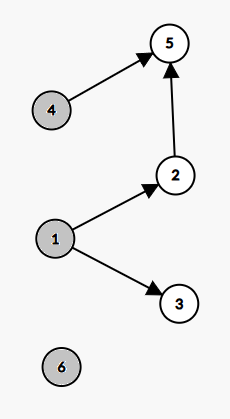
먼저 첫 학기에 선수 과목이 없는 과목 1, 4, 6을 수강했다고 하면 두 번째 학기에는 2, 3 과목을 수강할 수 있게 된다

이를 그래프적으로 생각해 탐색을 수강이라고 하고, 탐색을 하려면 인접하고 진입 가능한 노드가 탐색되어야 탐색이 가능하다고 볼 수 있다

따라서 조건에 맞는 1, 4, 6번 노트가 탐색이 되었고, 1번 노드가 탐색되었기 때문에 2, 3번 노드가 탐색이 가능해졌음

그리고 선수 과목인 1번을 수강했기 때문에 2, 3번의 선수 과목의 갯수가 줄었으므로 2, 3번의 진입 차수가 1번 노드가 탐색되었을 때 1 감소 되었다고 볼 수 있음

즉 노드를 탐색하면 그 노드와 이어진 다음 노드의 진입 차수를 감소 시킨다

여기서 다음 노드의 진입 차수가 0이 되어서 탐색이 가능하다면 선수 과목을 수강했기 때문에 과목이 수강 가능해진 것이기 때문에 다음 학기에 수강되어야 한다

이 조건에 따라 탐색이 몇 단계에 걸쳐 이루어졌는지 확인하면 그 단계가 과목을 수강할 수 있는 최소 단계가 됨

소스 코드

import java.io.*
import java.util.*

fun main(){
    val br = BufferedReader(InputStreamReader(System.`in`))
    var st = StringTokenizer(br.readLine())
    val N = st.nextToken().toInt()
    val M = st.nextToken().toInt()
    val result = IntArray(N + 1)
    val graph = ArrayList<ArrayList<Int>>()
    val prerequisite = IntArray(N + 1){0}
    for(i in 0..N){
        graph.add(arrayListOf())
    }
    for(i in 1..M){
        st = StringTokenizer(br.readLine())
        val u = st.nextToken().toInt()
        val v = st.nextToken().toInt()
        graph[u].add(v)
        prerequisite[v] += 1
    }
    val queue = ArrayDeque<IntArray>()
    for(i in 1..N){
        if(prerequisite[i] == 0){
            queue.add(intArrayOf(i, 1))
        }
    }
    while (queue.isNotEmpty()){
        val temp = queue.poll()
        val u = temp[0]
        val level = temp[1]
        if(prerequisite[u] == 0){
            result[u] = level
            for(v in graph[u]){
                prerequisite[v] -= 1
                if(prerequisite[v] == 0){
                    queue.add(intArrayOf(v, level + 1))
                }
            }
        }
    }
    for(i in 1..N){
        print("${result[i]} ")
    }
}