백준 15681번: 트리와 쿼리

문제: https://www.acmicpc.net/problem/15681

문제 풀이

DP + DFS

dp[N] = N을 루트로 하는 서브 트리의 정점 수

$dp[N] = \sum{dp[V]} + 1$ ($V$는 $N$의 자식노드)

위의 식에 따라 루트 노드에서부터 DFS와 memoization을 이용해 dp 테이블을 구하고 쿼리에 맞게 출력하면 정답

풀이 설명

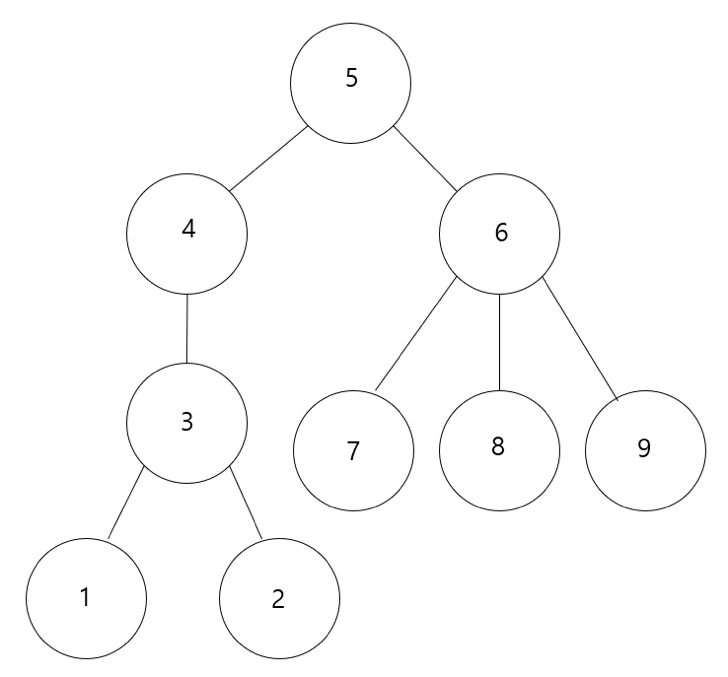
문제 예시처럼 이런 트리가 있다고 할 때 5번 노드를 부모 노드라고 하면 4번, 6번 노드가 자식 노드가 된다.

그리고 이 때 5번 노드를 루트로 하는 트리의 정점 수는 4번 노드를 루트로 하는 서브 트리의 정점 수와 6번 노드를 루트로 하는 서브 트리의 정점 수에 5번 노드를 더한 값이 된다는 것을 알 수 있다.

즉 특정 노드를 루트로 하는 서브 트리의 정점 수는 그 노드의 자식 노드를 루트로 하는 서브 트리의 정점 수의 합에 특정 노드를 더한 값이 된다.

이를 구하기 위해 루트 노드에서부터 DFS를 이용해 모든 자식 노드의 dp값을 현재 노드의 dp값에 더해주면 모든 노드에 대해 특정 노드를 루트로 하는 서브 트리의 정점 수를 구할 수 있다.

이렇게 구한 값들을 쿼리에 맞게 출력하면 정답.

소스 코드

import java.util.StringTokenizer

fun main(){
    val br = System.`in`.bufferedReader()
    var st = StringTokenizer(br.readLine())
    val N = st.nextToken().toInt()
    val R = st.nextToken().toInt()
    val Q = st.nextToken().toInt()
    val graph = Array(N + 1){ArrayList<Int>()}
    for(i in 1 until N){
        st = StringTokenizer(br.readLine())
        val U = st.nextToken().toInt()
        val V = st.nextToken().toInt()
        graph[U].add(V)
        graph[V].add(U)
    }
    val dp = IntArray(N + 1){1}
    solve(dp, graph, R, R)
    for(i in 1..Q){
        println(dp[br.readLine().toInt()])
    }
}

fun solve(dp: IntArray, graph: Array<ArrayList<Int>>, current: Int, parent: Int): Int{
    if(graph[current].size == 1 && current != parent){
        return dp[current]
    }
    for(v in graph[current]){
        if(v == parent) continue
        dp[current] += solve(dp, graph, v, current)
    }
    return dp[current]
}