백준 1613번: 역사

문제: https://www.acmicpc.net/problem/1613

문제 풀이

플로이드 워셜 알고리즘을 사용

dp[i][j] = i보다 j가 먼저 일어났는지 여부

• 먼저 일어났으면 -1, 모르면 0, 늦게 일어났으면 1

사건 i, j, k가 있을 때 i가 k보다 먼저 일어났고, k가 j보다 먼저 일어났으면 i가 j보다 먼저 일어난 사건이 됨

따라서 dp[i][k] == dp[k][j] == -1일 경우 dp[i][j]에 -1 대입

반대로 i가 k보다 늦게 일어났고, k가 j보다 늦게 일어났으면 i가 j보다 늦게 일어난 사건이 됨

이 경우 dp[i][k] == dp[k][j] == 1일 경우 dp[i][j]에 1 대입

모든 k에 대해 과정을 반복하면 답을 구할 수 있음

풀이 설명

일부 사건의 전후 관계를 알고 있을 때 특정 사건의 전후 관계를 알 수 있는지를 확인하는 문제

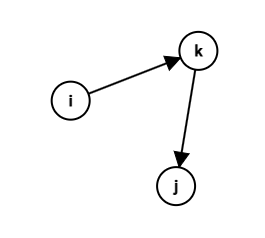
예를 들어 i가 k보다 먼저 일어났고, k가 j보다 먼저 일어났다는 일부 사건의 전후 관계를 알고 있을 때 특정 사건 i와 j의 전후 관계를 알 수 있는지를 보자. 3단 논법을 통해 i가 j보다 먼저 일어났다는 점을 알 수 있을 것이다.

따라서 i와 j의 전후 관계를 모르는 상태에서 알려면 i, j와 전후 관계가 확실한 사건 k가 필요하다.

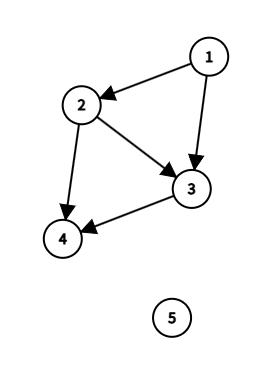
예시를 방향 그래프로 나타면 이렇게 되고, 방향을 사건이 일어난 순서라고 했을 때 일부 사건의 전후 관계를 위의 사진처럼 그래프로 나타냈을 때 특정 사건 i, j의 전후 관계를 찾는 일은 i 에서 j 까지 또는 j 에서 i 까지를 그래프의 특정 점을 거쳐서 탐색할 수 있는지가 된다.

따라서 그래프에서 특정 점을 거쳐 최단 경로를 찾는 플로이드 워셜 알고리즘을 사용해 그래프 탐색 여부를 구하면 문제를 해결할 수 있다.

소스 코드

import java.io.BufferedReader
import java.io.BufferedWriter
import java.io.InputStreamReader
import java.io.OutputStreamWriter
import java.util.StringTokenizer

fun main(args: Array<String>){
    val br = BufferedReader(InputStreamReader(System.`in`))
    val bw = BufferedWriter(OutputStreamWriter(System.out))
    var st = StringTokenizer(br.readLine())
    val n = st.nextToken().toInt()
    val k = st.nextToken().toInt()
    val dp = Array(n+1){IntArray(n+1){0}}
    for(i in 1..k){
        st = StringTokenizer(br.readLine())
        val i = st.nextToken().toInt()
        val j = st.nextToken().toInt()
        dp[i][j] = -1
        dp[j][i] = 1
    }
    for(k in 1..n){//플로이드 워셜은 경유 지점을 기준으로 실행되어야 한다
        for(i in 1..n){
            for(j in 1..n){
                if(dp[i][k] == -1 && dp[k][j] == -1){
                    dp[i][j] = -1
                } else if(dp[i][k] == 1 && dp[k][j] == 1){
                    dp[i][j] = 1
                }
            }
        }
    }
    val s = br.readLine().toInt()
    for(i in 1..s){
        st = StringTokenizer(br.readLine())
        val x = st.nextToken().toInt()
        val y = st.nextToken().toInt()
        bw.write("${dp[x][y]}\n")
    }
    bw.flush()
    bw.close()
    br.close()
}