백준 2565번: 전깃줄

문제: https://www.acmicpc.net/problem/2565

문제 풀이

dp

전깃줄을 A 기준으로 오름차순 정렬 후 나오는 B의 위치에서 가장 긴 증가하는 부분수열을 구하면 교차하지 않는 전깃줄의 최대 갯수를 구할 수 있음구하면 교차하지 않는 전깃줄의 최대 갯수를 구할 수 있음

가장 긴 증가하는 부분수열을 구하기 위해 dp 알고리즘 사용

dp[i]를 i 번째 요소를 포함하는 가장 긴 증가하는 부분 수열이라고 하면

dp[i] = i 번째 요소 보다 앞에 있는 요소들 중 i 번째 요소보다 작은 요소의 dp값 중 최댓값 + 1

모든 i에 대해 dp 테이블을 구하고 테이블의 최댓값을 구하면 최대 전깃줄 갯수이므로 n에서 그 값을 빼면 정답

풀이 설명

없애야 하는 전깃줄의 최소 개수는 전체 전깃줄에서 교차되지 않게 최대한 많이 연결한 전깃줄의 개수를 뺀 값과 같음

따라서 교차되지 않게 최대한 많이 전깃줄을 연결하면 됨

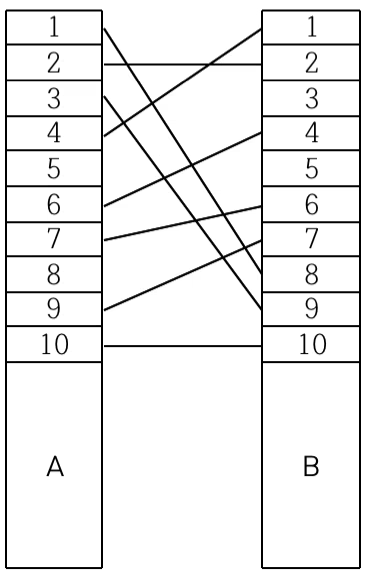
예시와 같은 상황이 있을 때 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄을 x, A의 2번 위치와 B의 2번 위치를 잇는 전깃줄을 y라고 하면

A의 위치를 살펴봤을 때 x, y의 순서를 보면 x가 1, y가 2로 오름차순이고, B의 위치를 보면 x가 8, y가 2이므로 내림차순이다

따라서 두 전깃줄이 교차하려면 A의 위치와 B의 위치 순서가 달라야 함으로, A의 위치와 B의 위치 순서가 같은 가장 긴 부분 수열을 구하면 됨

이에 따라 교차하지 않는 전깃줄의 최대 개수를 구하려면 먼저 A의 위치를 기준으로 전깃줄을 오름차순으로 정렬했을 때의 B의 위치에서 A의 위치와 순서가 같게 오름차순으로 가장 긴 부분수열을 구하면 되고 이는 증가하는 부분수열이 됨

예시 상황에 따라 A의 위치를 기준으로 정렬한 B의 위치는 [8, 2, 9, 1, 4, 6, 7, 10] 이고

이 때 가장 긴 증가하는 부분수열이 [2, 4, 6, 7, 10]이고 전깃줄이 5개 이므로 답이 3이 됨

소스 코드

import java.util.StringTokenizer

fun main(){
    val br = System.`in`.bufferedReader()
    val n = br.readLine().toInt()
    val map = Array(n + 1){IntArray(2)}
    for(i in 1..n){
        val st = StringTokenizer(br.readLine())
        map[i][0] = st.nextToken().toInt()
        map[i][1] = st.nextToken().toInt()
    }
    map.sortWith { o1, o2 -> o1[0] - o2[0]}
    val dp = IntArray(n + 1){1}
    for (i in 2..n){
        var max = 0
        for(j in 1 until i){
            if(map[i][1] > map[j][1]){
                if(max < dp[j]){
                    max = dp[j]
                }
            }
        }
        dp[i] = max + 1
    }
    var max = 0
    for(i in 1..n){
        if (max < dp[i]) max = dp[i]
    }
    println(n - max)
}