백준 28127번: 숫자탑과 쿼리

문제: https://www.acmicpc.net/problem/28127

문제 풀이

이분 탐색

curStart = 현재 층의 첫 블록의 숫자

curStart가 x보다 작거나 같은 층의 최댓값을 찾아 그 층과, 그 층에서 x가 몇 번째 블록인지 출력하면 정답.

풀이 설명

첫 층에 a개의 블록이 있고, 첫 층의 가장 왼쪽 블록이 1이고 오른쪽으로 갈 수록 숫자가 1 높아지고, 다음 층의 가장 왼쪽 블록은 현재 층의 가장 오른쪽 블록의 숫자보다 1 높고, 현재 층의 블록 개수보다 다음 층의 블록 개수가 d개 많은 상황일 때 각 층의 가장 왼쪽 블록의 숫자를 다음과 같이 구할 수 있다.

$1 + a \times (floor - 1) + d \times (floor - 1) \times (floor - 2) \div 2$

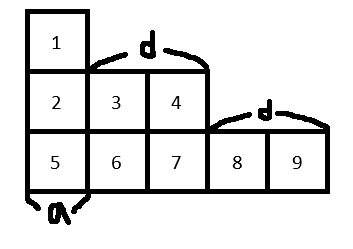
예제 상황의 a = 1, d = 2 일때의 블록을 다시 보면 이렇게 볼 수 있다. 여기서 보면 각 층의 가장 첫 블록은 그 전 층까지의 블록 갯수 합에 1을 더한 값이 된다는 것을 알 수 있다. 그리고 매 층마다 항상 a개의 블록이 있고, 2층부터 층을 내려갈때마다 d개의 블록이 추가되므로 이를 윗층까지의 블록의 갯수를 두 부분으로 나눠 a개의 블록의 합 $a \times (floor - 1)$ 와 추가되는 d개의 블록의 합 $d \times (floor - 1) \times (floor - 2) \div 2$으로 나타낼 수 있다.

따라서 층마다 가장 왼쪽 블록의 숫자를 알 수 있기 때문에 이 블록이 x보다 작거나 같은 숫자 중 최대한 크게 되는 숫자의 층이 x가 존재하는 층의 가장 왼쪽 블록이므로, 이를 이분 탐색으로 찾으면 층을 더 빠르게 구할 수 있다.

이때 a와 d가 1,000,000 이하이므로 계산할 때 Int 범위를 벗어날 수 있기 때문에 Long으로 계산을 해준다. 그리고 x도 1,000,000 이하이므로 층이 가장 높게 될 때는 a = 1, d = 1일 때 대략 1500이하가 되기 때문에 이분 탐색할 때 최대 층을 1500정도로 잡아도 된다.

이 문제는 질문 개수가 500,000개 이하이므로 입출력이 상당히 많다. 따라서 출력을 print로 바로 하지 말고 StringBuilder를 쓰거나 BufferedWriter를 사용하지 않으면 시간초과가 된다. 이에 주의해서 이분 탐색으로 구한 층과 그 층에서의 x의 위치를 출력하면 정답이 된다.

소스 코드

import java.util.StringTokenizer

fun main(){
    val br = System.`in`.bufferedReader()
    val q = br.readLine().toInt()
    val sb = StringBuilder()
    repeat(q){
        val st = StringTokenizer(br.readLine())
        val a = st.nextToken().toLong()
        val d = st.nextToken().toLong()
        val x = st.nextToken().toLong()
        var left = 1L
        var right = 1500L
        while(left <= right){
            val mid = (left + right) / 2
            val curStart = 1 + a * (mid - 1) + d * (mid - 1) * (mid - 2) / 2
            if(curStart > x){
                right = mid - 1
            } else {
                left = mid + 1
            }
        }
        val start = 1 + a * (right - 1) + d * (right - 1) * (right - 2) / 2
        sb.append("$right ${x - start + 1}\n")
    }
    print(sb)
}