백준 1520번: 내리막길

문제: https://www.acmicpc.net/problem/1520

문제 풀이

DP의 Memoization 기법과 dfs를 같이 사용해 문제를 풀 수 있다.

dp[x][y] = x, y 부터 목표 지점까지 도달할 수 있는 경로의 수 (-1은 아직 탐색되지 않았음을 뜻함)

시작점에서 dfs를 통해 문제 조건에 맞게 내리막길로 목표 지점에 도달 가능한 경로를 찾는다.

이 때, 경로를 탐색하며 dp 테이블의 값이 -1이 아니라면 이미 그 점에서 목표 지점까지 경로를 찾아본 것이기 때문에 더 이상 탐색할 필요가 없이 값만 가져와 답을 구한다.

풀이 설명

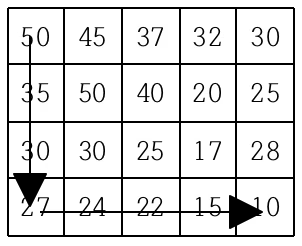
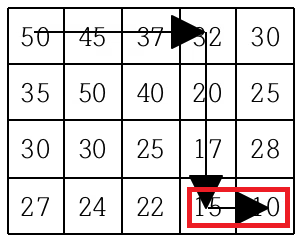
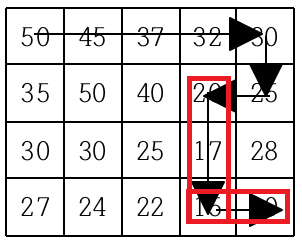
문제 예시에는 이렇게 3가지 경로가 있다. 일반적인 dfs로 문제를 풀어본다고 가정하면
일단 첫번째 이미지처럼 경로를 찾았다고 치자, 두 번째 경로를 탐색할 때 이미 첫 번째 경로에서 탐색한 두 점을 다시 탐색하게 된다. 세 번째 경로를 찾을 때도 마찬가지로 첫 번째 경로와 두 번째 경로에서 이미 탐색한 점을 다시 탐색하게 된다는 문제가 있다.

따라서 DP의 Memoization 기법을 이용해 먼저 탐색했던 점에서의 결과 값을 저장해놓고 그 점에 도달할 때 다시 탐색하지 않고 값을 사용하는 것으로 반복 횟수를 줄일 수 있다.

소스 코드

import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.StringTokenizer

val dx = arrayOf(-1, 0, 1, 0)
val dy = arrayOf(0, -1, 0, 1)

fun main(args: Array<String>){
    val br = BufferedReader(InputStreamReader(System.`in`))
    var st = StringTokenizer(br.readLine())
    val N = st.nextToken().toInt()
    val M = st.nextToken().toInt()
    val map = Array(N){IntArray(M)}
    val dp = Array(N){IntArray(M){-1}}
    for (i in 0..<N){
        st = StringTokenizer(br.readLine())
        for (j in 0..<M){
            map[i][j] = st.nextToken().toInt()
        }
    }
    solve(0, 0, N, M, map, dp)
    println(dp[0][0])
}

fun solve(x: Int, y: Int, N: Int, M: Int, map: Array<IntArray>, dp: Array<IntArray>): Int{
    if(x == N - 1 && y == M - 1){
        return 1
    }
    if (dp[x][y] != -1){
        return dp[x][y]
    }
    dp[x][y] = 0
    for(i in 0..3){
        val nx = x + dx[i]
        val ny = y + dy[i]
        if(nx in 0..<N && ny in 0..<M){
            if(map[x][y] > map[nx][ny]){
                dp[x][y] += solve(nx, ny, N, M, map, dp)
            }
        }
    }
    return dp[x][y]
}