Big O 란?
좋은 코드의 조건
좋은 코드의 조건은 무엇이 있을까
- Readable : 읽고 이해할 수 있는가?
- Efficiency: 메모리를 효율적으로 사용하는가?
- Scalable : input 의 규모가 커져도 느려지지 않는가?
우선 가독성이 좋아야하고, 메모리를 많이 차지하지 않으며, input 의 양이 많아져도 대응이 가능해야 할 것이다.
Big O 는 코드가 Scalable 한 코드인지, 알고리즘을 수행할 때 시간이 얼마나 걸리는 지 측정할 때 사용하는 일종의 언어이다.
컴퓨터의 메모리는 한정적이기 때문에 효율적인 관리가 필요한데 이 때 필요한 개념은 공간 복잡도이다.
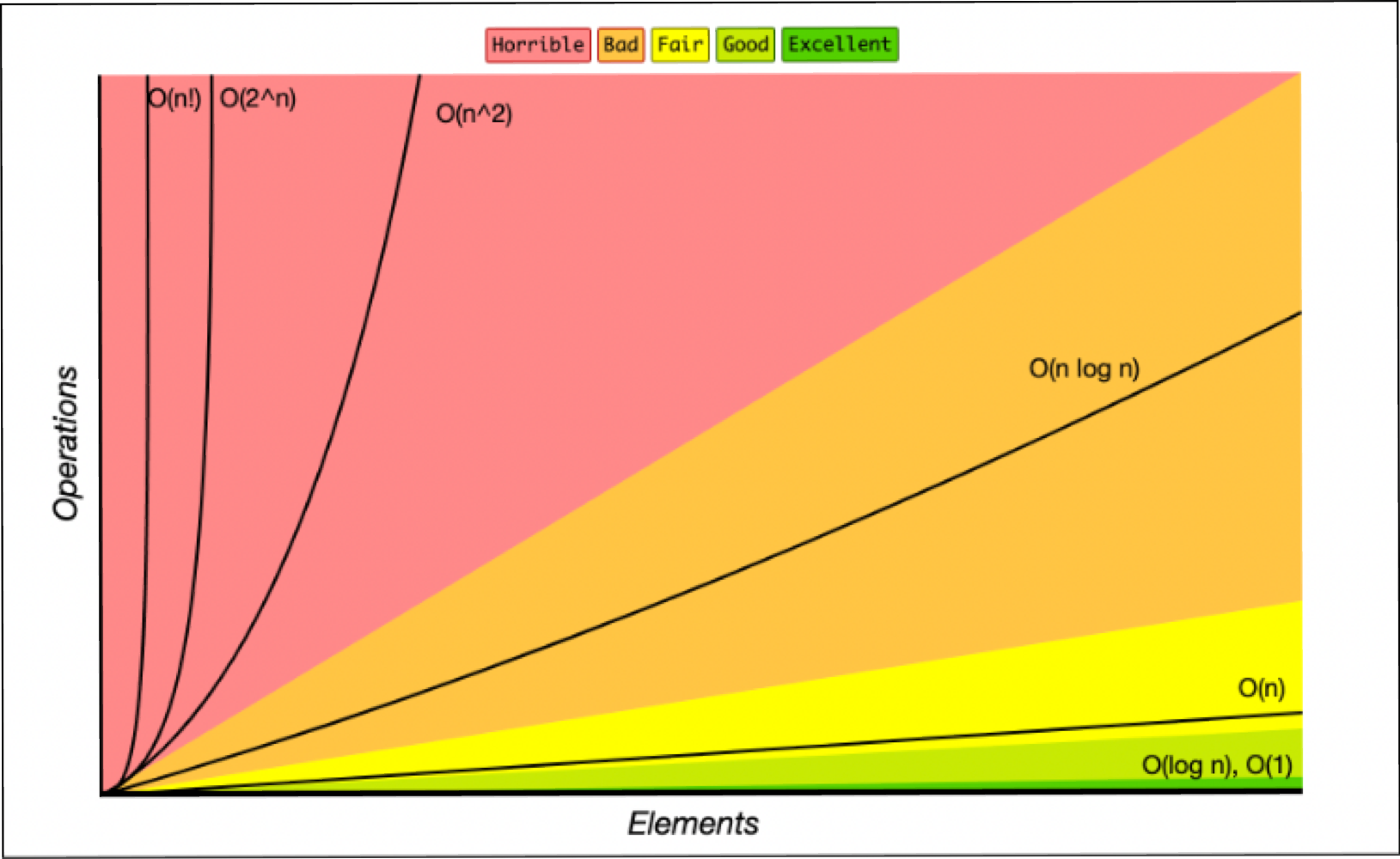
위에 보이는 그래프는 Big O 차트이다.
input 되는 element 의 양에 따라 작업량 (operation)이 얼마나 늘어나는지 나타난 그래프이다.
많은 사람들이 오해하는 것이 Big O 는 작업이 수행되는데 얼마나 걸리는 지에 대한 것이 아니라, input 의 증가에 따라 runtime 이 얼마나 빨리 증가하는지를 측정하는 것이다.
이 개념이 오늘 포스트 중에 가장 중요한 것 같다.
몇가지만 살펴보자면
O(n): Linear Time
const everyone = ['dory', 'bruce', 'marlin', 'nemo', 'gill', 'bloat', 'nigel', 'squirt', 'darla', 'hank'];
findNemo = (array => {
for (let i = 0; i < array.length; i++) {
if (array[i] === 'nemo') {
console.log("Found NEMO");
}
}
});
findNemo(everyone);findNemo 함수의 Big O 를 계산해보면, input 인 배열의 길이가 10 이므로 해당 함수는 10번 동작한다. 즉 input 되는 element 의 개수와 작업의 수가 선형으로 증가하는데 이러한 경우를 Linear Time, O(n) 이라고 한다.
O(1): Constant Time
const boxes = [0,1,2,3,4,5,6];
function logFirstTwoBoxes(boxes) {
console.log(boxes[0]); // O(1)
console.log(boxes[1]); // O(1)
}
logFirstTwoBoxes(); // O(2)위의 경우는 input 아무리 많아져도 작업 횟수는 2회이다. 하지만 O(2), O(3), O(100) 같은 경우에도 input 의 증가와는 별개이므로 모두 O(1) 이다.
O(n^2): Quadratic Time
// Log all pairs of array
const boxes = ['a','b','c','d','e'];
function logAllPairsOfArray(array) {
for (let i = 0; i < array.length; i++) {
for (let k = 0; k < array.length; k++) {
console.log(array[i], array[j]);
}
}
}
logAllPairsOfArray(boxes);O(n^2) 의 경우 인터뷰에서 자주 마주칠 수 있는데, 보통 반복문이 중첩된 경우이다. 따라서 Big O 에서 n x n 이므로 n^2 이다.
O(n!)
O(n!) 은 모든 element 에 전부 nested loop 이 적용된 구조이다. 가장 비효율적이며 안좋은 코드이다.
이것들 외에도 몇 종류의 Big O 가 더 존재한다.
O(1) Constant- no loops
// O(log N) Logarithmic- usually searching algorithms have log n if they are sorted (Binary Search)
O(n) Linear- for loops, while loops through n items
// O(n log(n)) Log Liniear- usually sorting operations
O(n^2) Quadratic- every element in a collection needs to be compared to ever other element. Two nested loops
// O(2^n) Exponential- recursive algorithms that solves a problem of size N
// O(n!) Factorial- you are adding a loop for every element
Iterating through half a collection is still O(n)
Two separate collections: O(a * b)주석 처리한 것들은 자료구조와 알고리즘을 더 배울 때 등장한다.
Big O 계산 규칙
Rule 1 : Worst Case
Rule 2 : Remove Constants
Rule 3 : Diffent terms for inputs
Rule 4 : Drop Non Dominants
Worst Case
Big O 계산할 때는 최악의 상황을 고려하라는 규칙이다.
const nemo = ['nemo'];
const everyone = ['dory', 'bruce', 'marlin', 'nemo', 'gill', 'bloat', 'nigel', 'squirt', 'darla', 'hank'];
const large = new Array(10000).fill('nemo');
findNemo = (array => {
for (let i = 0; i < array.length; i++) {
if (array[i] === 'nemo') {
console.log("Found NEMO");
}
}
});
findNemo(everyone);위 코드에서 nemo 를 찾기 위해서는 10번의 작업이 필요하다. 실제 nemo 는 배열의 네번 째 위치하지만 10번의 작업을 끝까지 실행한다.
const nemo = ['nemo'];
const everyone = ['dory', 'bruce', 'marlin', 'nemo', 'gill', 'bloat', 'nigel', 'squirt', 'darla', 'hank'];
const large = new Array(10000).fill('nemo');
findNemo = (array => {
for (let i = 0; i < array.length; i++) {
if (array[i] === 'nemo') {
console.log("Found NEMO");
break; // 여기를 추가!
}
}
});
findNemo(everyone);이를 해결하기 위해 break 를 사용하여 nemo 를 찾았을 때 반복문을 멈추도록 코드를 작성하였다.
하지만 그래도 Big O 는 O(n) 이다. 위의 코드는 코드의 효율성을 위해 작성된 것이다.
Big O 는 Worst Case를 가정하여 nemo 가 배열의 맨 끝에 있을 때로 가정해야한다.
이렇게 최악의 상황을 고려하면 input 이 되는 element 의 개수 증가에 따라 작업 횟수도 선형적으로 증가하기 때문에 위 경우 O(n) 이 된다.
Remove Constants
말 그대로 상수를 제거하라는 규칙이다.
function printFirstItemThenFirstHalfThenSayHi100Times(items) {
console.log(items[0]); // O(1)
var middleIndex = Math.floor(items.length / 2);
var index = 0;
while (index < middleIndex) { // O(n/2)
console.log(items[index]);
index++;
}
for (var i = 0; i < 100; i++) { // O(100)
console.log('hi');
}
}위 코드에서 Big O 를 계산하면 O(1 + n/2 + 100) 이다.
최악의 경우를 가정하여 n 이 만약 1억일 때, 1억을 2로 나눈 것에 1과 100을 더하건 의미가 없기 때문에 상수를 제거하여 O(n) 이다.
또한 O(2n) 같은 경우도 Big O 는 코드 계산 속도에 대한 것이 아니며, 아무리 가파르거나 완만해도 선이 일직선이기만 하면 선형이다.
Diffent Terms for Inputs
input 이 다른 경우 각각 Big O 계산을 해야한다.
function compressBoxesTwice(boxes, boxes2) {
boxes.forEach(function(boxes) { // O(a)
console.log(boxes);
});
boxes2.forEach(function(boxes2) { // O(b)
console.log(boxes);
});
}위의 코드는 각각 다른 input 을 받아 와 작업을 수행하기 때문에 각각 a,b 로 하여 Big O 는 O(a+b) 이다.
Drop Non Dominants
function printAllNumbersThenAllPairsSums(numbers) {
console.log('these are the numbers');
numbers.forEach(function(number) { // O(n)
console.log(number);
});
console.log('and these are their sums');
numbers.forEach(function(firstNumber) {
numbers.forEach(function(secondNumber) {
console.log(firstNumber + secondNumber); // O(n^2)
});
});
}
printAllNumbersThenAllPairsSums([1,2,3,4,5]);위에서 Big O 를 계산하면 O(n + n^2) 이다.
상수를 제거하라는 규칙과 마찬가지로 n^2 에 비해 지배적이지 못한 n 를 제거해주어 O(n^2) 으로 표기한다.
공간 복잡도
시간 복잡도가 input 이 되는 element 대비 작업 횟수의 증가를 보는 것이라면, 공간 복잡도는 작업 수행시 공간을 얼마나 추가로 사용하는 지 보는 것이다.
공간 복잡도에 영향을 미치는 요소
- 변수
- 자료구조 (Data Structure)
- 함수 호출 (Function Call)
- 할당 (Allocation)
function booo(n) {
for (let i = 0; i < n.length; i++) {
console.log('booo!');
}
}
booo([1,2,3,4,5]);공간 복잡도를 계산할 때, input 이 얼마나 큰지는 크게 중요하지 않다. 하지만 특정 작업 내에서 메모리 공간을 얼마나 사용하는지 본다.
위의 코드는 반복문에서 변수 i 를 선언한 것 이외에는 공간복잡도에 영향을 미치는 작업이 없기 때문에 공간복잡도는 O(n) 이다.
function arrayOfHiNTimes(n) {
let hiArray = [];
for (let i = 0; i < n; i++) {
hiArray[i]='hi';
}
return hiArray;
}
arrayOfHiNTimes(6); // O(n)위 코드에서는 for 문 내에서 배열에 값의 할당이 n 번 일어났기 때문에 공간복잡도는 O(n) 이다.
자료구조와 알고리즘 공부가 필요한 이유
내가 개발하고자 하는 하나의 프로그램은 자료구조와 알고리즘의 조합이다.
자료구조는 데이터를 저장하는 방법이며, 알고리즘은 저장된 데이터를 꺼내 사용하는 것이다. 개발하는 과정에서 기능 구현이 중요한 일 중 하나지만, 개발자가 필요한 이유는 얼마나 효율적인 코드 (빠르고 메모리를 덜 잡아먹는) 를 짜는 지가 중요하다고 생각한다. 속도와 공간을 효율적으로 사용하는 것은 결국 어떤 문제를 해결하기 위해 올바른 자료구조형을 가져와 효율적인 알고리즘으로 구현하는 것이기에 자료구조와 알고리즘을 공부해야하는 이유라고 생각한다.

