[Algorithm] Binary Search, 이진(이분) 탐색

이진 탐색이란?

이진 탐색은 정렬된 리스트에서 검색 범위를 줄여 나가면서 검색 값을 찾는 알고리즘이다.

후에 방식을 보면 이해하겠지만 반드시 정렬된(오름차순, 내림차순) 데이터에만 적용할 수 있는 탐색 알고리즘이다.

• 장점: 검색이 반복될 때마다 검색 범위가 절반으로 줄기 때문에 속도가 빠르다.
• 단점: 정렬된 리스트에만 사용할 수 있다.

동작 방식

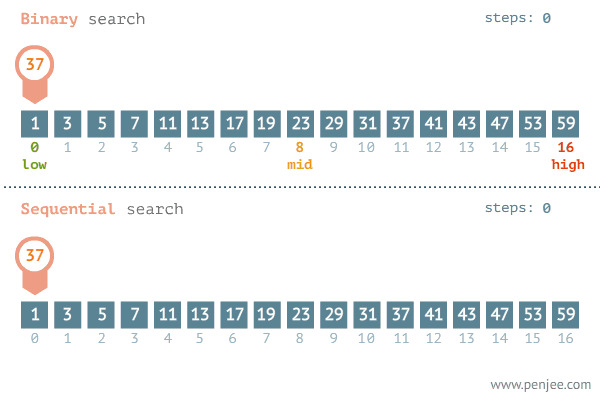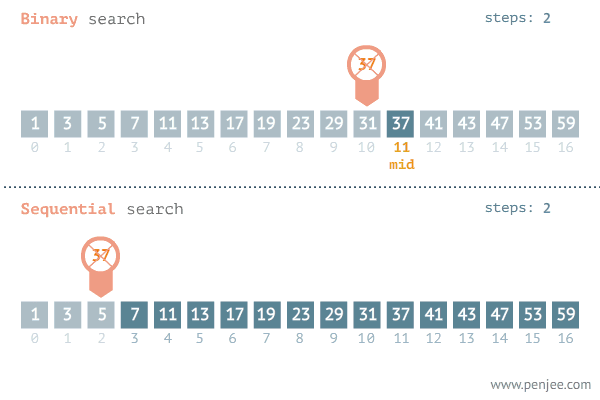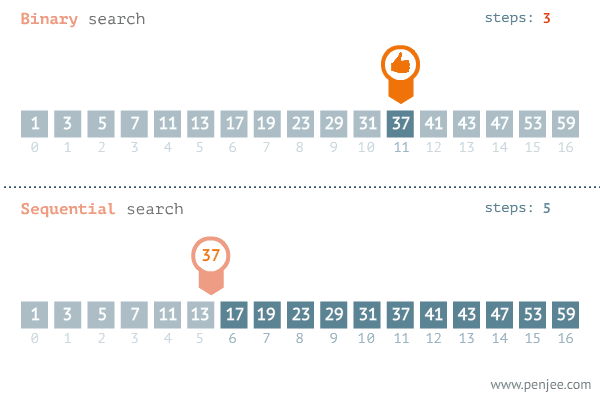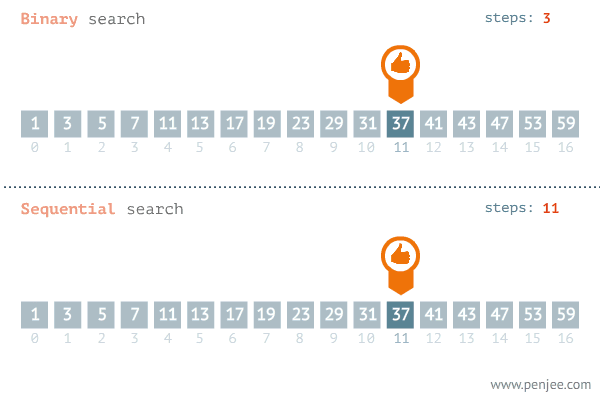
1. 배열의 중간 값 확인
2. 중간 값과 검색 값을 비교
   2.1. 중간 값이 검색 값이 같다면 종료
   2.2. 중간 값보다 검색 값이 크다면 중간 값 기준 오른쪽을 탐색
   2.3. 중간 값보다 검색 값이 작다면 중간 값 기준 왼쪽을 탐색
3. 더 이상 값을 찾을 수 없을 때까지 반복

구현

반복문을 이용한 방법

• javascript code

  // ary: 탐색할 배열, low: 왼쪽 포인터, high: 오른쪽 포인터, goal: 검색 값
  
  const binarySearch = (ary, low, high, goal) => {
      while(low <= high) {
          const mid = low + (high - low) / 2;
  
          if(arr[mid] === goal) return mid;		// 검색 성공
          if(arr[mid] < goal) low = mid + 1;
          if(arr[mid] > goal) high = mid - 1;
      }
  
      return -1;									// 검색 실패
  }

• java code

  // ary: 탐색할 배열, low: 왼쪽 포인터, high: 오른쪽 포인터, goal: 검색 값
  
  public int binarySearch(int ary[], int low, int high, int goal) {
      while(low <= high) {
          int mid = low + (high - low) / 2;
  
          if(arr[mid] == goal) return mid;		// 검색 성공
          if(arr[mid] < goal) low = mid + 1;
          if(arr[mid] > goal) high = mid - 1;
      }
  
      return -1;									// 검색 실패
  }

재귀 함수를 이용한 방법

• javascript code

  // ary: 탐색할 배열, low: 왼쪽 포인터, high: 오른쪽 포인터, goal: 검색 값
  
  const binarySearch = (ary, low, high, goal) => {
      if(low > high) return -1;											// 검색 실패
  
      const mid = low + (high - low) / 2;
  
      if(arr[mid] === goal) return mid;									// 검색 성공
      if(arr[mid] < goal) return binarySearch(arr, low, mid - 1, goal);
      if(arr[mid] > goal) return binarySearch(arr, mid + 1, high, goal);
  }

• java code

  // ary: 탐색할 배열, low: 왼쪽 포인터, high: 오른쪽 포인터, goal: 검색 값
  
  public int binarySearch(int ary[], int low, int high, int goal) {
      if(low > high) return -1;											// 검색 실패
  
      int mid = low + (high - low) / 2;
  
      if(arr[mid] == goal) return mid;									// 검색 성공
      if(arr[mid] < goal) return binarySearch(arr, low, mid - 1, goal);
      if(arr[mid] > goal) return binarySearch(arr, mid + 1, high, goal);
  }

+) 중간 값 구하는 방식

위 구현은 다음 방식을 사용하였다.

int mid = low + (high - low) / 2

다음과 같이 간결하게 사용하면 되지 않을까?

int mid = (low + high) / 2

두번 째 방식에서 low + high 값이 Integer 범위보다 크다면 음수 값으로 오버플로우 될 것이고 해당 값을 2로 나누면 mid는 음수가 되기 때문에 탐색에 문제가 된다.

그렇기 때문에 low + high의 값이 범위를 벗어난다면 첫번째, 그렇지 않다면 연산이 간단한 두번째 방식을 채용하는 것이 효율적이다.

시간 복잡도

Best의 경우 빠른 시간내로 값을 구할 수 있지만 최악의 경우 데이터가 하나 남을 때 까지 탐색한다.

• BEST CASE

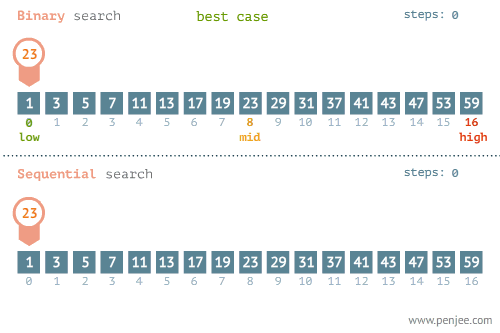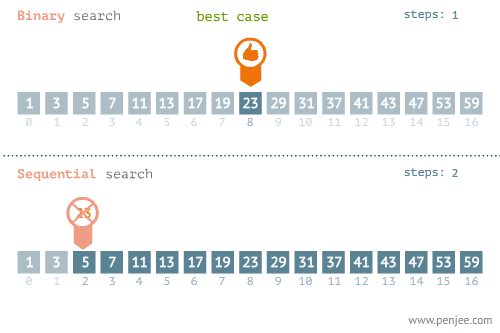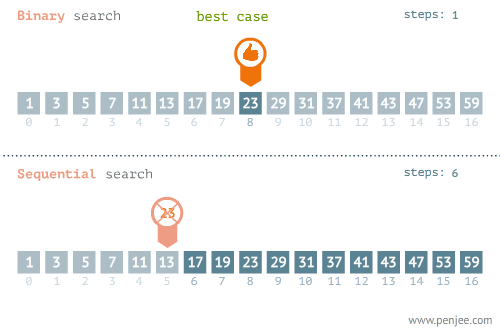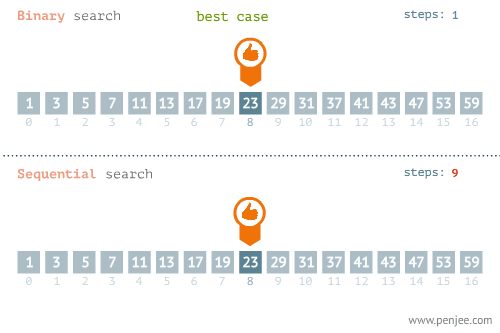
• WORST CASE

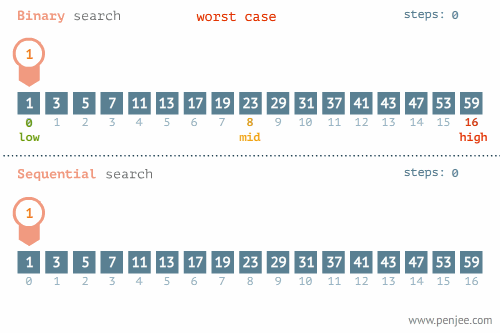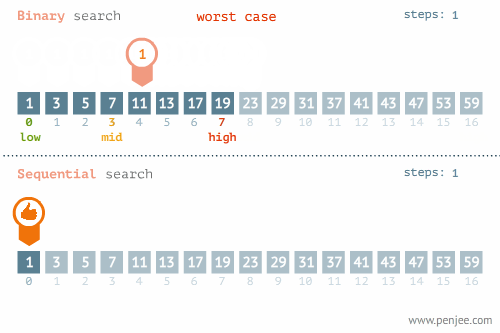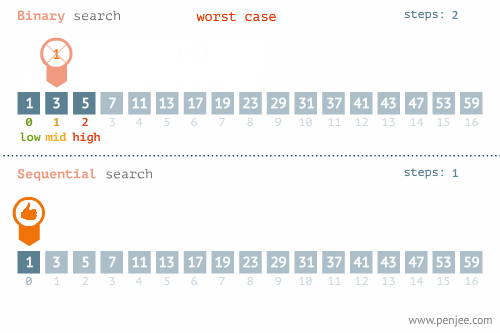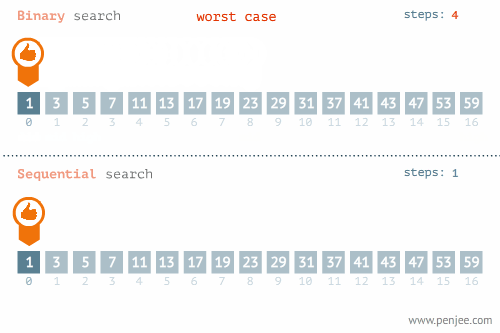
시간 복잡도를 계산해 보자.

1. 첫번째 탐색 후 절반만 남은 수는 $N\over2$개
2. 쭉 탐색을 하면 n번째 탐색일 때는 $N\over2$개에 $1\over2$를 $n-1$번 곱한 것과 같다.
   ex) 3번째 탐색 : $N \over 2$$\times$$1 \over 2$$\times$$1 \over 2$
3. 규칙을 찾아 수식으로 나타내면 k번째 탐색에서 남은 데이터 수는 ($1\over2$)$^k$$\times N$이 된다.
4. 이때 우리가 구해야 할 최악의 경우는 ($1\over2$)$^k$$\times N = 1$이다.
5. 위의 식 양변에 $2^k$를 곱하고 다시 양변에 $log_2$를 취하면 최종 식은 $k = log_2N$이 된다.

따라서 이진 탐색의 시간 복잡도는 $O(log_2N)$이다.