
제목에서도 보이겠지만, 저는 transition과 animation만 학습하면 어느정도는 됐다! 싶었습니다.
하지만 제 편견과 오만.. 막상 학습한 것을 적용하여 그리니에게 움직임을 주려니 제가 배우지 않은 가장 중요한게 있더라고요.
바로 transform!
저는 그리니에게 들숨날숨의 들썩임, 앉았다 일어났다의 움직임. 날개 퍼덕임 등등을 주려 했습니다.
그러기 위해선 제가 만든 svg태그를 찌그러트리고 기울이고를.. 했어야 했는데, transition과 animation으로 하기에는 제한되는 부분이 있더구만요.
그래서! 진짜진짜 찐막. 사실 또 이런게 있을 것 같긴 한데, 암튼 transform을 공부해보겠습니다.
transform
위에서도 말했듯, transform 속성은 해당 요소를 찌그러트리고, 늘리고, 기울이고, 위치를 옮기고.. 등등을 할 수 있습니다.
흔히 있는 일은 아니지만, 부모요소(둘러 쌓은 박스)의 크기를 조절하면 그에 맞게 자식 요소가 늘어지거나 줄어드는 효과를(비율을 유지하지 않은) 적용하고 싶을 때가 있을 겁니다.
그때! CSS 속성인 transform을 적용하면 아주 쉽게 해결 할 수 있습니다.
그래도 비교적, 다른 애니메이션 속성에 비해서는 쉬운편이라고 생각합니다.
transition과 animation 속성도 궁금하다면 링크를 참고해주세요.
transform 속성
transform 속성에는 크게 5가지가 있습니다. 바로 표로 보시죠.
| 속성 | 설명 | 기본 값 |
|---|---|---|
| matrix(a, b, c, d, e) | 나머지 4개의 속성을 행렬 테크닉을 통해 간결하게 표현할 수 있습니다. | 1,0,0,1,0,0 |
| translate(a, b) | 중심 좌표를 기준으로 x,y 거리를 통해 위치를 설정합니다. | 0, 0 |
| scale(a, b) | 요소의 크기의 배율을 설정하여 늘리거나 줄입니다. | 1, 1 |
| rotate(a) | 평면 상 기울기 각도를 설정합니다. | 0 |
| skew(a, b) | x축과 y축을 기준으로 기울기 각도를 설정합니다. | 0, 0 |
뭔가.. 알듯 말듯..
여기까지 보신다면 당연히 이해하기 힘들죠.
하나씩 살펴봅시다!
우선 matrix는 행렬을 어떻게 적용하는지 알아야하기 때문에 translate먼저 보시죠.
translate
translate는 중심점(0, 0)을 기준으로 위치를 설정할 수 있는 속성입니다.
transform: translate(10%, -20px);위에서 볼 수 있듯이, 단위는 %와 px 등 css내에서 길이를 정하는 단위면 가능합니다.
저는 중심점을 기준이라고 말씀드리는데, 다른 글이나 자료에서는 요소(박스)의 윗 라인과 왼쪽 라인을 기준으로 위치를 정한다고 설명을 해주시더라고요.
저는 중심점이 더 이해하기 쉬워서 이렇게 설정했습니다.
그러면 중심점은 어디냐? 당연하게 요소의 중앙입니다.
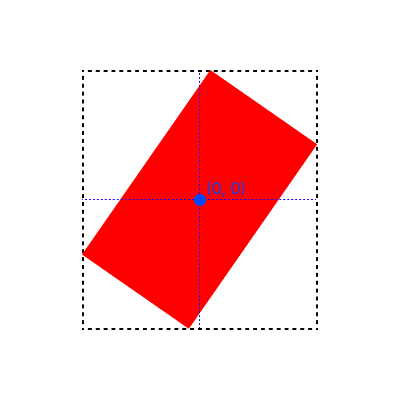
위 그림에서 보이듯, 중심점은 선택자로 지정한 요소(그림에서의 점선 박스)를 기준으로 지정된다고 보시면 됩니다.
그 안의 빨간 박스 요소가 기준이 아니라는 점만 아시면 될 것 같습니다.
그러면 어떻게 설정하면 어디로 갈까요?
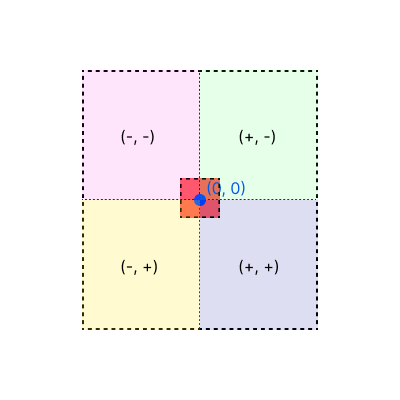
조금은 이해가 가시나요?
왼쪽 위에서부터 오른쪽 아래 방향으로 값이 커진다고 보시면 됩니다.
위의 예시를 실제로 구현해본다면!
이런식으로 나옵니다.
어렵지않죠? 왼쪽 아래에 삐져나간 요소는, 실제로 부모 요소 밖에까지 적용이 된다는 점을 보여줍니다.
scale
scale은 양옆, 위아래로 얼만큼 늘리고 줄일지 결정합니다.
transform: scale(3, 4);두개의 값을 넣을 수 있는데, 첫번째 값은 좌우, 두번째 값은 위아래로, 몇 배수로 크기를 조절할지 정합니다.
특징은 다음과 같습니다.
- 실수, 정수 모두 입력할 수 있습니다. 즉 0이나 0.xx, 음수까지도 가능합니다.
- 기본적으로 두개의 값이 들어가나 임의로 하나의 값을 넣으면 좌우, 위아래 동일한 값으로 적용됩니다.
웬지 양수만 가능할 것 같은데.. 0이나 음수나 가능한게 신기하지 않나요?
우선 0보다 큰 값부터 봅시다.
이렇듯, 적용된 숫자에 따라 변화하는 크기를 볼 수 있습니다.
여기서 볼 수 있는 특징이 두가지 있는데요.
바로
-
늘리듯이, 혹은 찌그러트리듯이 변한다는 점.
덕분에 요소에 있는 글자나 그 어떤 것이든 비율, 형태가 보장되지 않습니다.
-
요소의 위치에 영향을 끼치지 않는다는 점.
각각의 요소에 margin을 다르게 설정해 주었습니다. 이유는 요소들이 서로 위치는 그대로인데, 유독 커진 요소덕분에 겹치게 되어 보기 좋게 떨어트리기 위해서 엿습니다.
즉, 요소가 커진다고 해서 위치가 변하는 것은 아니며, z-index나 선언 순서에 따라 요소가 겹칠 수도 있습니다.
그렇다면 0을 넣으면 어떻게 될까요?
제가 위에서 배수로 적용된다고 말한 것을 기억하시나요? 맞습니다. 0을 곱하면 그 어떤 것도 보이지 않을 것입니다.
이것은 코드를 작성해도 의미가 없으니 궁금하면 직접 해보세요!
근데 음수는? 과연 어떻게 될까요
간단히 예를 들어 x,y 그래프 위에 (0, 3) 좌표가 있다고 가정해 봅시다.
해당 좌표의 x, y에 -3을 곱하면 어떻게 될까요?
(0, -9)가 되겠죠?
커지는 것은 둘째치고 (0, 0)을 기점으로 반대 방향으로 이동할 것입니다.
scale도 동일합니다! 결과를 직접 보시죠.
보이시나요? -2를 설정해주자 2배로 커짐과 동시에 글자를 보면 알 수 있듯이 중앙 점을 기점으로 반전된 모습이 보입니다.
흔한 상황은 아니지만, 만약 다음과 같이 요소를 돌려야 할 상황에서는 코드 한줄로 손쉽게 적용할 수 있겠죠.
rotate
어려울 것이 전혀 없는 속성이죠. 그냥 돌리는 겁니다! 피자 도우 돌리듯이..
transform: rotate(45deg);보시다 시피 돌리고 싶은 각도를 설정합니다. 이 때 양수는 시계방향, 음수는 반시계 방향으로 회전합니다.
값으로는 deg, rad 단위의 수를 넣을 수 있습니다.
직접 보시죠!
0을 넣으면 어떻게 되냐고요? 아무일도 일어나지 않습니다!
단위를 적지 않으면 어떻게 되냐고요? 아무일도 일어나지 않습니다!
겨우 반례 2개 추가하기 귀찮냐고요? 네!
skew
skew는 평면상 돌렸던 rotate의 피자도우와는 다르게 x축 y축을 기준으로 돌려버리는 공중에 뜬 피자 도우입니다.
transform: skew(30deg, 20deg);rotate와 들어가는 값의 조건은 동일합니다.
값으로는 deg, rad 단위의 수를 넣을 수 있고, 양수는 시계방향, 음수는 반시계 방향으로 회전합니다.
사실 말로만 들어선 x축 y축을 기준으로 돌리는게 어떤 의미인지 감이 안잡히실수도 있습니다.
메커니즘을 보시죠!
- x축 기준 회전
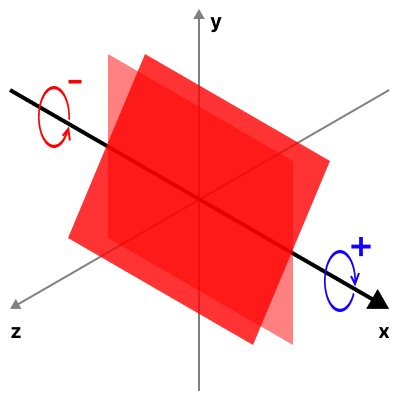
- y축 기준 회전
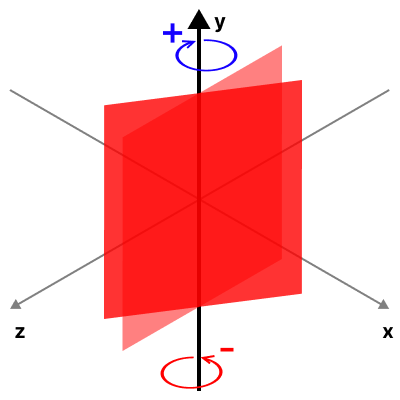
조금은 이해가 가시나요?
2개의 값을 통해 각각 축을 기준으로 얼만큼 회전할지 정한다고 생각하시면 됩니다!
예시를 보시죠.
어렵죠? 한개의 축만 생각해도 머리가 복잡한데 2개의 축의 회전을 신경써야하니,,
이건 직접 다뤄보고, 어떻게 하면 얼만큼 회전을 하나.. 익히는 수 밖에는 없을 것 같습니다.
제가 짠 코드와 출력되는 결과를 보기만 한다면 의미 없겠죠?
matrix
matrix는 속기형 비스무리 한 것입니다.
엄밀히 말하자면 속기형이라기 보다 간결히 표현하는 또 하나의 속성. 이라고 볼 수 있겠네요.
그게 속기형 아니냐고요? 비슷한 의미이긴 하죠.
속기형과 구분해서 말하는 이유는 transition이나 animation의 속기형 표현 처럼 단지 속성 값들을 나열해서 적는게 아니라 matrix는 행렬의 계산 태크닉도 알아야하기 때문입니다.
참고로 transform은 속형이 따로 없고 여러개를 적용하고 싶다면 다음과 같이 그냥 나열해서 적으면 됩니다.
transform: perspective(500px) translate(10px, 0, 20px) rotateY(3deg);직접 보시죠!
transform: matrix(a, b, c, d, e, f);위의 6개의 값으로 지금 까지 본 4가지 속성을 모두 표현할 수 있습니다!
각각 무엇을 의미하는지 볼까요?
| 위치 | 의미 | 설명 |
|---|---|---|
| a | scaleX | scale의 x값을 설정합니다. |
| b | skewY | skew의 y값을 설정합니다. |
| c | skewX | skew의 x값을 설정합니다. |
| d | scaleY | scale의 y값을 설정합니다. |
| e | translateX | translate의 x값을 설정합니다. |
| f | translateY | translate의 y값을 설정합니다. |
의문이 생길겁니다. 아니 rotate는 어디있는거지?
물론 있습니다! 그전에 제가 왜 행렬을 알야하한다고 했는지 알아볼까요?
위 6개의 값은 다음과 같이 표현 할 수 있습니다.

행렬을 배운 분들이라면 어렵지 않게 이해 할 수 있을 겁니다.
이 때 scale, skew, translate의 기본값을 넣어본다면?
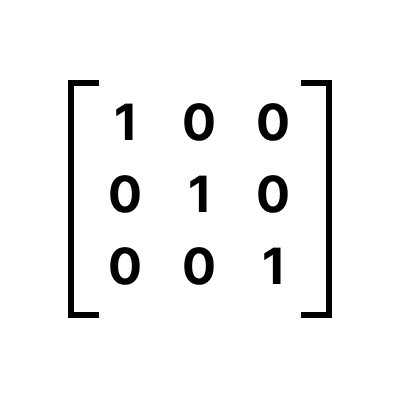
위 값이 바로 matrix 속성의 기본 형태입니다.
하지만 뭔가 의문이 있죠. 마지막 줄은 왜 '0 0 1'일까? 이 이유는 조금 더 뒤에서 설명드리겠습니다!
우선 가장 급한 것부터 해결합시다. 도대체 rotate는 어떻게 표현하냐? 다음과 같습니다.
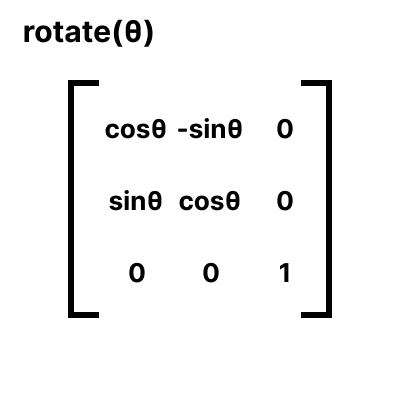
머리가 아프신가요?
어렵게 생각할 것 없습니다. 위에서 말하고자 하는건
'scale(cosθ)와 skew(-sinθ, sinθ)를 주면 rotate(θ)를 주는 것과 같다!' 입니다.
역시 증명해야겠죠?
보시면 알다시피, 'matrix(3con45, 2sin45, -3sin45, 2con45, 0, 0)' 이런 아름다운 값으로 넣을 순 없습니다.
허용하는건 실수, deg,, 등등으로 제한되어 있으니까요.
하지만 확실한건 저렇게라도 넣으면 똑같이 작동한다는 점이겠죠?
다음으로 봐야할 것은, 그럼 여러개의 속성은 같이 처리 할 수 있나? 입니다.
있습니다!
예를 들어 scale(2, 3)과 rotate(45deg)를 같이 적용하고 싶다면? 이 때 행렬의 곱을 사용합니다.
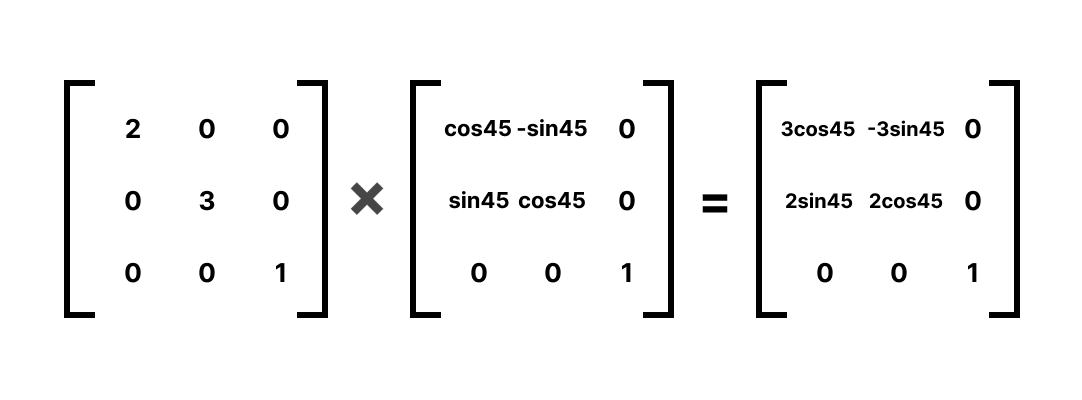
이런식으로요.
여기서 주의해야 할 점이 있습니다.
과연 아래의 2개는 같은 결과를 보일까요?
transform: scale(2, 3) rotate(45deg);
transform: rotate(45deg) scale(2, 3);행렬에 익숙하신 분들이라면 답을 이미 알고있을 겁니다.
뭐, 직접 보시죠.
네. 다릅니다.
이유는 하나밖에 없죠. 바로 행렬의 곱은 순서에 따라 다른 값이 나오기 때문입니다!
이 부분은 행렬과 행렬의 곱에 대해 알아야 이해할 수 있는 부분입니다. 본문에서는 따로 다루지 않으니 따로 학습 후 다시 보시길 바랍니다.
무튼 결론은 속성을 나열하든, matrix를 사용하든 이부분을 유의해서 사용하면 되겠습니다.
마지막으로 의문점 회수해야겠죠!
첫번째 두번째 줄의 '1 0 0', '0 1 0'이야 기본 값이니 그러려니 하죠.
하지만 마지막 줄이 '0 0 1'인 이유. 그 이유는 위에서 말한 행렬 곱. 때문입니다.
저희는 3번째 열이 translate를 의미한다는 것을 알죠? 분명 이부분도 행렬의 곱에 영향을 받을 것 입니다.
그런데 만약 마지막 줄이 '0 0 0'이라면?
영문도 모른채 0이 되버리는 일이 발생하겠죠.
3번째 열의 값을 보존하기 위해 '0 0 1'을 사용하는 것 입니다. 이 또한 행렬의 곱을 알고 있어야 하기 때문에, 행렬 학습 후 봐주세요.
transform-origin
끝인 줄 알았지만, 마지막 하나가 남았습니다.
주 속성은 아니지만 유용하게 쓰이는 속성을 소개하려 합니다.
바로 중심점의 위치를 조절할 수 있는 속성!
돌이켜 보면 transform은 중심점을 기준으로 동작하는 애니메이션이라고 해도 무방합니다.
모든 기준이 중심점이고 이것을 옮김에 따라 색다른 애니메이션이 나오니까요.
기본적으로 중심점은 말 그대로 요소의 정중앙입니다.
이것을 어떻게 옮길 수 있을까요?
바로 transform-origin!
transform-origin의 기본 값은 다음과 같습니다.
transform-origin: 50%, 50%
/* transform-origin: center */50%, 50%. 말 그대로 요소의 너비와 높이의 절반 위치가 중심점입니다. 이는 center이라고 적어도 똑같이 적용되죠.
그렇다면 0%는 어디일까요? 쉽게 그림으로 보죠.
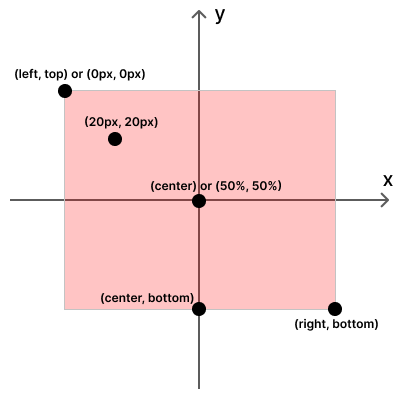
보다시피 왼쪽 위가 0%, 즉 기준 점이라고 볼 수 있습니다.
px, % 단위 뿐만 아니라 center, left, right, top, bottom 등의 위치를 표현하는 단어로 설정할 수도 있습니다.
그렇다면 이렇게 중심 점을 옮기면 어떤 차이가 있을까요?
확연히 차이가 있죠.
이걸 어디에 써먹어야 하나 싶지만, 중심 점 차이가 보기에 좀 더 편안한 애니메이션을 만든다고 생각합니다.
여유가 있다면 어디에 중심점을 적용해야 하나 고민해 보면 좋겠죠!
마치며
조금은 아쉬운 글입니다.
왜냐면 제가 본문에서 다룬 transform은 절반도 안되거든요..
rotate나 scale 같은 속성도 rotateX, scaleY같은 부가적인 속성도 있고 transform-origin과 같이 transform-box, transform-style 속성으로 좀 더 디테일한 부분을 설정할 수도 있기 때문이죠.
게다가 오늘 다룬 내용은 '2D' 애니메이션을 다루는 transform입니다. 이말은 당연하게도 '3D'도 다를 수 있는 속성이 있다는 거죠.
우선은 제가 필요한 2D transform을 학습하여 포스팅 해보았는데요. 기회가 되면 좀 더 깊게 다른 속성들도 공부해 볼 생각입니다.
다음은 이것을 적용한 그리니의 모습으로 돌아왔으면 좋겠네요.