[Algorithm] 그래프(Graph)

그래프(Graph)의 개념

노드(N ,node)와 그 노드를 연결하는 엣지(E, edge)를 하나로 모아놓은 자료구조이다. 연결되어 있는 어떤 것을 표현할 때 사용하는 자료구조이다.

그래프에 관한 용어

Node or Vertex (N or V) : 여러가지 특성을 가질 수 있는 객체(정점).
Edge (E) : 노드들 사이를 연결시켜 주는 선.
Path: 노드에서 노드로 가는 경로.
Simple Path: 경로상의 노드들이 겹치지 않는 경로.
cycle: Simple Path중 시작 노드와 끝 노드가 동일한 경우.
Subgraph: 큰 Graph 집합안에 있는 graph
Spanning Graph: Subgraph중 Graph의 node를 모두 포함하고 있는 graph.
Tree: connected하지만, cycle이 없는 경우.

그래프의 종류

Directed Graph VS Undirected Graph

• Directed Graph
  노드를 연결해주는 선에 방향이 있어, 정의된 방향으로만 움직이는 것이 가능.
  (D,E)와 (E,D)가 다르다.
• Undirected Graph
  노드를 연결해주는 선에 방향이 없어, 노드간의 선이 존재한다면, 어느 방향으로든지 움직일 수 있다.
  (D,E)와 (E,D)가 동일하다.

Symmetric Digraph

• Directed Graph에서, 두 노드간의 edge가 존재해, 서로 왕래 할 수 있는 그래프.
  Node D,E 사이에 (D,E)와 (E,D)가 모두 존재한다.

Complete Graph

• Undirected Graph에서, 모든 node들이 서로 연결되어 있는 그래프.

Connected Graph

• Graph에서 모든 Node사이에 경로가 존재하는 그래프.

그래프 탐색

너비 우선 탐색(BFS)

• 한 노드에서 시작해서 다른 노드로 넘어갈때, 시작 노드의 인접한 노드들을 모두 찾고 넘어가는 방법.

1. 시작 노드의 가장 가까운 인접 노드부터 탐색하고, 점점 멀리 있는 노드들을 탐색하는 방법.
2. 하나의 분기를 깊게(depp) 탐색하는 것이 아닌, 하나의 노드에서 넓게(wide) 탐색하는 방법.
3. 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 사용하는 방법.
4. 시작 노드에서 시작하여 거리에 따라 탐색하는 방법.

특징

1. 구현을 할 때 FIFO(First In First Out)을 사용하는 queue를 사용하여 구현한다.
2. DFS와는 다르게 재귀적 방법을 사용하지 않는다.
3. 시간 복잡도

• 모든 node를 queue에 넣는 시간 복잡도: O(V)
• 모든 node를 dequeue하는 시간 복잡도: O(V)
• 모든 edge 탐색하는 시간 복잡도: O(E)
  총 : O(V+E)

깊이 우선 탐색(BFS)

• 한 노드에서 한 브랜치에 모든 부분을 탐색하고 다른 브랜치로 넘어가 탐색하는 방법.

1. 넓게(wide) 탐색하는 것이 아닌, 깊게(deep) 탐색하는 방법.
2. 모든 노드를 방문하고자 할 때, 해당 방법을 사용한다.

특징

1. 재귀적으로 구현한다.(stack와 같은 원리)
2. 만약 해당 노드에서 더 이상 탐색할 노드가 없다면, 전의 노드로 backtrack하여, 탐색할 노드가 있는지 본다.
   3.시간 복잡도

• 모든 node 탐색: O(V)
• 모든 edge 탐색: O(E)
  총 : O(V+E)

[BFS VS DFS]

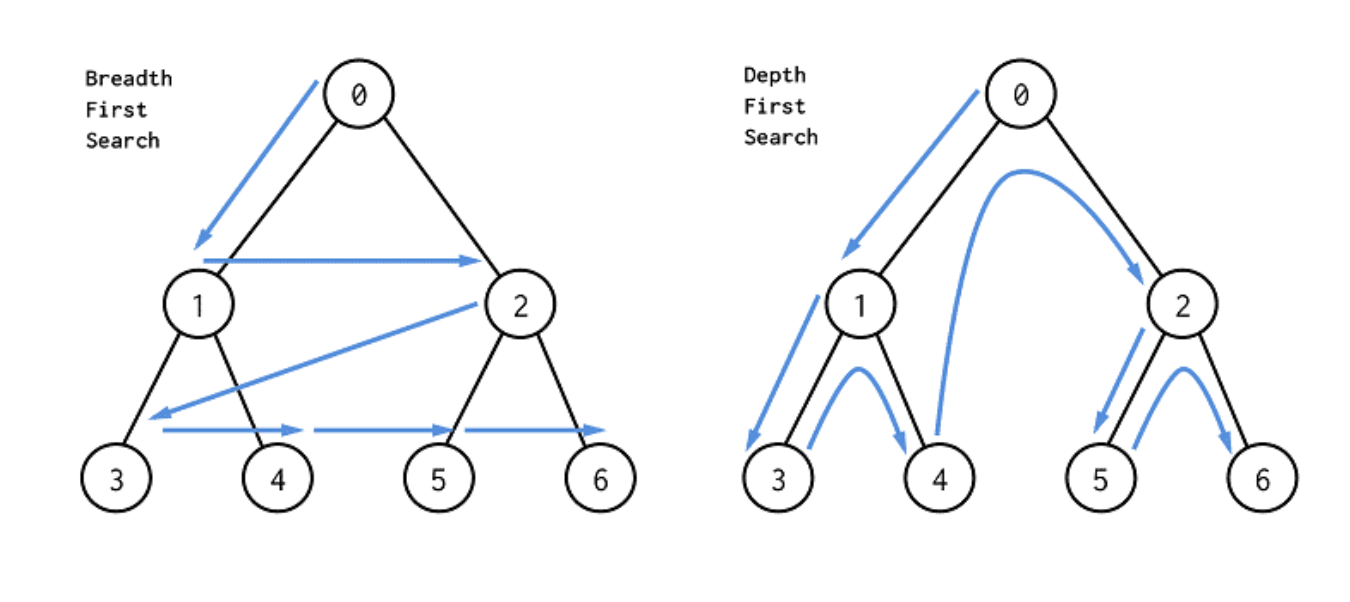
[출처: http://dawoonjeong.com/algorithm-graph-bfs-dfs/]