data-structure
1주차
오성: https://velog.io/@monsterkos/TIL2020.08.01
준수: https://www.notion.so/kljopuu/0fbf4ebd52d04f5d816c8d986f399283?v=6188fbb861554aa1b6b836add46f12ae
질문 위주의 학습
Q.
1. 배열이란?
2. 파이썬에서 배열 기능을 제공하는 것은?
3. 배열의 장점과 단점은?
4. 큐(Queue)란?
enqueue, dequeue를 알아두자
5. 큐의 대표적인 활용예시는?
6. 스택(Stack)이란?
push, pop을 알아두자
7. 스택의 활용예시는?
8. 스택의 장단점?
9. 배열과 linked list의 차이는?
10. linked list의 노드와 포인터에 대해 설명하세요.
11. linked list를 파이썬으로 구현해보세요.
12. 링크드 리스트의 단점은?
13. linked list와 double linked list의 차이점은?
14. 알고리즘 복잡도 계산은 왜 하는 것인지 설명하세요.
15. 시간 복잡도와 공간 복잡도에 대해 설명하세요. (어떤게 더 많이 쓰이는지 포함해서)
16. 알고리즘 시간 복잡도는 000이 지배한다.
17. 가장 대표적인 알고리즘 성능 표기법 Big O(빅-오) 표기법에 대해 설명하세요.
18. Big O에서 O(1), O(n), O(n제곱) 을 예시를 들어 설명하세요.
19. hash, hash table, hashing function에 대해 차이점을 중심으로 각각 설명하세요.
20. 파이썬에서 해쉬 테이블로 이루어진 지료구조는?
21. 해쉬 테이블의 장점과 단점은 무엇인가요?
22. 해시 테이블의 시간 복잡도는?
23. 해시 테이블의 주요 용도는 무엇인가요?
24. 슬롯이 5칸인 해쉬테이블을 구현해보세요
조건(해쉬 함수: key % 5, 해쉬 키 생성: hash(), 슬롯은 list로 만들기)
25. 해시 테이블의 가장 큰 문제인 충돌(collision)은 어떤 현상인가요?
26. Collision을 해결하는 대표적 2가지 방법을 설명하세요.
27. 이진 트리(binary Tree)와 이진 탐색 트리(Binary Search Tree, BST)의 차이는 무엇인가요?
28. 힙(Heap)이 무엇이고 왜 사용하는지(장점) 최댓값 혹은 최솟값을 찾을 때의 시간복잡도를 사용하여 설명하시오.
29. 힙과 이진 탐색 트리의 공톰점과 차이점을 설명하시오.
30. 힙에서 데이터 삽입 또는 삭제시의 시간 복잡도는?
A.
1.데이터를 나열하고, 각 데이터를 인덱스에 대응하도록 구성한 데이터 구조. 같은 종류의 데이터를 효율적으로 관리 하기 위해 사용.
같은 종류의 데이터를 순차적으로 저장
2. 리스트
3. 장점: 빠른 접근 가능(인덱스), 단점: 데이터 추가/삭제의 어려움(미리 최대 길이 지정해야 함)
4. FIFO(first-in, first-out). 줄을 서는 것.
5. "운영체제에서 멀티 태스킹을 위해 프로세스 스케쥴링을 구현할 때 쓰입니다"
6. LIFO(last-in, first-out). 쌓인 책.
7. 프로세스의 함수 동작 방식에서 쓰인다.
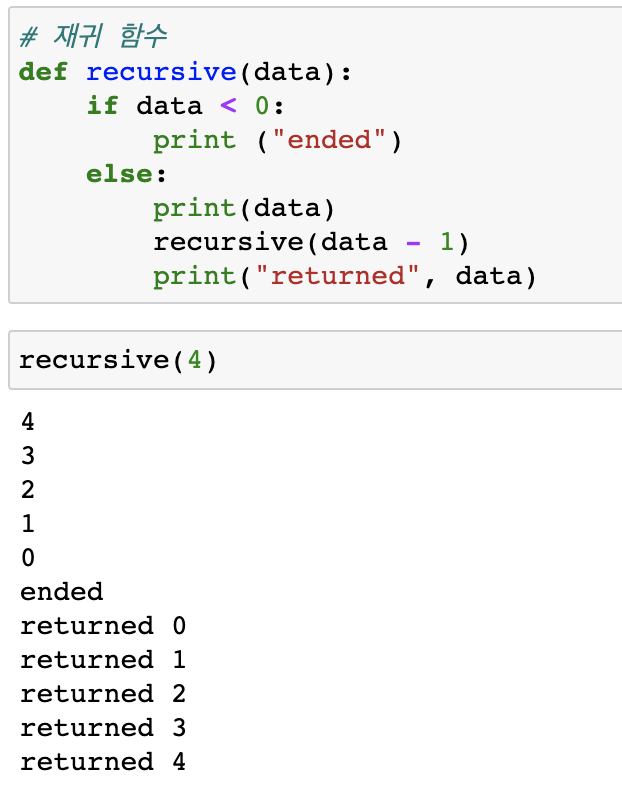
8. 장점: 1)구조가 단순해서 구현이 쉽다. 2)데이터 저장/읽기 속도가 빠르다.
단점: 1)데이터 최대 갯수를 미리 정해야 한다.(파이썬 재귀함수는 1000번까지만 호출 가능. 1000개까지만 공간을 확보해놨기 때문에 그 이상 호출하면 에러 발생)
2)저장 공간의 낭비가 발생할 수 있음(미리 최대 갯수만큼 저장 공간 확해야 함.)
- 배열은 순차적으로 연결된 공간에 데이터를 나열하는 구조인 반면, 링크드리스트는 떨어진 곳에 존재하는 데이터를 연결해 관리하는 데이터 구조. 배열은 미리 공간을 확보해놔야 하는 단점이 있는데 링크드리스트는 이를 보완한다.
- 노드는 데이터 값-포인터로 이루어진 데이터 저장 단위, 포인터는 다음 혹은 이전 노드의 주소를 저장하는 공간.
class Node:
def __init__(self, data, next=None):
self.data = data
self.next = next
class NodeMgmt:
def __init__(self, data):
self.head = Node(data)
def add(self, data):
if self.head == "":
self.head = Node(data)
else:
node = self.head
while node.next:
node = node.next
node.next = Node(data)
def desc(self):
node = self.head
while node:
print(node.data)
node = node.next
def delete(self, data):
if self.head =="":
print("해당 값 가진 노드는 없습니다.")
return
if self.head.data == data:
temp = self.head
self.head = self.head.next
del temp
else:
node = self.head
while node.next:
if node.next.data == data:
temp = node.next
node.next = node.next.next
del temp
return
else:
node = node.next
linkedlist1 = NodeMgmt(0)
for data in range(1,10):
linkedlist1.add(data)
linkedlist1.desc()
print("====")
linkedlist1.delete((3))
linkedlist1.desc()
-
1)주소정보를 위한 별도 데이터 공간이 필요하기에, 저장공간 효율이 리스트에 비해 낮다.
2) 연결 정보를 찾는데 시간을 쓰므로 접근 속도가 느리다.
3) 중간 데이터 삭제시, 앞뒤 데이터의 연결을 재구성해야 해서 비효율적이다. -
double linked list는 [이전 노드 주소] - [데이터] -[다음 노드 주소]로 이루어져있다. linked list는 무조건 데이터를 앞에서부터 찾아가야 하는 단점이 있었다. 노드가 총 1000개인데 찾고자 하는 데이터가 맨 마지막에 있다면 1000번을 검색해야 가능하다. 이런 단점을 보완하기 위해 나온게 double linked list로, 뒤에서부터도 검색이 가능하다.
-
어떤 알고리즘이 더 좋은지 분석하기 위해. (하나의 문제를 해결하는 다양한 방법 존재)
-
시간 복잡도는 알고리즘 실행속도다. 공간 복잡도는 알고리즘이 사용하는 메모리의 사이즈다.
-
반복문. 변수 갯수, if문 갯수 등은 상대적으로 시간복잡도에 영향을 덜 미친다.
-
O(N)으로 표기한다 가장 많이/일반적으로 사용된다.
알고리즘 최악의 실행 시간을 표기한다(=아무리 최악이라도, 이정도의 성능은 보장한다는 뜻이기 때문)
-참고로 시간 복잡도는 가장 큰 것만 계산하고, 상수는 무시한다.
-2n일 경우 시간 복잡도는 O(n)이다.
-n + 10 일경우 시간 복잡도는 O(n)이다.
-n제곱 + n + 3일경우 시간 복잡도는 O(n제곱)이다.
- 1부터 n을 더한 값을 출력하는 함수를 만들 때,
1) 반복문을 만들어 n번만큼 반복문을 돈다면 시간복잡도는 O(n)이다.
def sum_all(n):
total = 0
for num in range(1, n + 1):
total += num
return total2) 반복문 없이 아래처럼 작성하면 n의 값과 관계없이 코드는 한 줄 수행되므로 시간복잡도는 O(1)이다.
def sum_all(n):
return int(n * (n + 1) / 2)3) (위의 문제랑 별개) 주어진 n으로 2중 for문을 돌리면 시간 복잡도는 O(n제곱)이다.
-
1) 해쉬(hash)는 임의 값을 고정 길이로 변환하는 것을 말한다.
2) 해쉬 테이블은 key에 value(데이터)를 저장하는 자료구조다.
3) 해쉬 함수(hashing function)는 '어떤 길이의 데이터를 입력해도 정해진 길이의 결과를 리턴하는 함수이다. -
딕셔너리
-
장점:
1)데이터 저장과 검색 속도가 빠르다.
2) 해쉬는 키와 매칭되는 데이터가 있는지(중복) 확인이 쉽다.
단점:
1) 일반적으로 저장공간이 좀더 많이 필요하다.
2) 여러 키에 해당하는 주소가 동일할 경우 충돌을 해결하기 위한 방법이 필요하다. (충돌 해결 알고리즘) -
일반적인 경우(Collision이 없는 경우)는 O(1)
최악의 경우(Collision이 모두 발생하는 경우)는 O(n)
- 검색이 많이 필요한 경우
- 저장, 삭제, 읽기가 빈번한 경우
- 캐쉬 구현시 (중복 확인이 쉽기 때문)
1) 먼저 5칸짜리 슬롯을 만든다.
2) 입력받은 key값을 0~4 중 하나로 변환한다.(5칸이므로 인덱스는 0~4).
구체적으로 얘기하면, a)key를 숫자화 한 다음에 b)5로 나눈 나머지를 구하는 방식을 취한다.
3) 구해진 index에 값을 넣는다.
4) 데이터를 읽을 땐 키만 input받아 데이터를 추출한다.
hash_table = [i for i in range(5)]
def get_key(key):
return hash(key)
def hash_func(key):
return key % 5
def store_data(key, value):
key = get_key(key)
hash_address = hash_func(key)
hash_table[hash_address] = value
def read_data(key):
key = get_key(key)
hash_address = hash_func(key)
return hash_table[hash_address] -
충돌은 해쉬함수를 통해 같은 hash_address를 얻게 될 때 발생하는 문제입니다.
(집은 하난데, 두 사람이 같은 집 주소를 배당받은 것) -
Chaining기법과 Linear Probing기법이 있습니다.
Chaining기법은 linked_list로 같은 주소를 할당받은 데이터를 뒤에 연결시켜 문제를 해결합니다.
해시 테이블 저장공간 외의 공간을 활용하는 기법입니다.
반면, Linear Probing기법은 해시 테이블 저장공간 안에서 문제를 해결하는 방법으로써,
충돌 발생시 해당 hash address의 다음 address부터 순차적으로 탐색해 제일 처음 나오는 빈공간에 데이터를 저장시킵니다. -
이진 트리는 노드의 최대 branch가 2개인 트리다. 이진 탐색 트리는 이진 트리이지만, 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 큰 값을 가진다는 추가 규칙을 갖는 트리이다.
-
데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
->완전이진트리란? 노드를 삽입할 때 왼쪽 노드부터 차례대로 삽입하는 트리
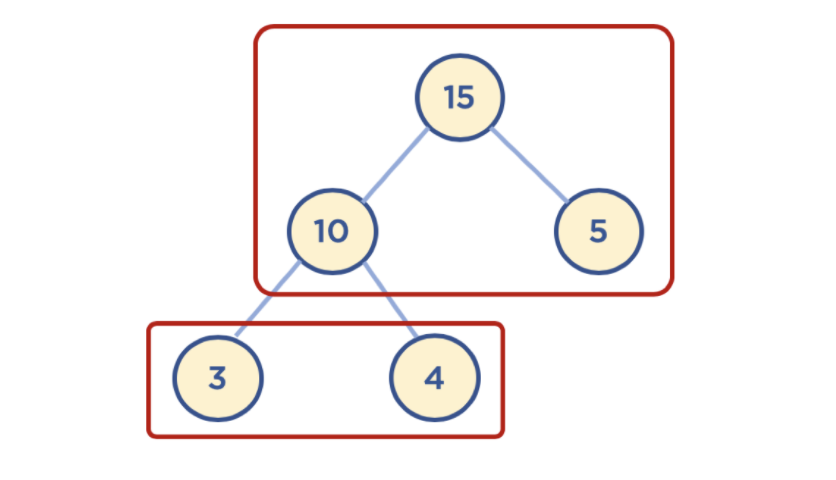
힙을 사용하는 이유
배열에 데이터를 넣고 최대, 최소값을 찾으려면 O(n)이 걸리는 반면, 힙에서는 O(logn)이 걸림.
-우선순위 큐와 같이 최대값 또는 최소값을 빠르게 찾아야 하는 자료구조 및 알고리즘 구현 등에 활용됨.
-
공통점: 둘 다 이진 트리이다.
차이점: -
힙은 각 노드의 값이 자식 노드보다 크거나 같음(max Heap의 경우)
-
이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고, 오른쪽 노드 값이 가장 큼
-
결론: 이진 탐색 트리는 탐색을 위한 구조, 힙은 최대/최소값을 검색하기 위한 구조
-
n개의 노드를 가지는 heap 에 데이터 삽입 또는 삭제시, 최악의 경우 root 노드에서 leaf 노드까지 비교해야 하므로 ℎ=𝑙𝑜𝑔2𝑛 에 가까우므로, 시간 복잡도는 𝑂(𝑙𝑜𝑔𝑛)
