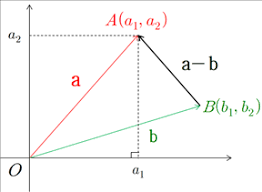
벡터의 내적(Dot product)은 벡터끼리의 연산으로 스칼라가 출력되는 연산이다.\quad a ⃗ ⋅ b ⃗ = [ a 1 a 2 ] ∙ [ b 1 b 2 ] = a 1 b 1 + a 2 b 2 = a ⃗ T b ⃗ \vec a \cdot \vec b=\begin{bmatrix} a_1 \\\\ a_2 \\ \end{bmatrix} \bullet \begin{bmatrix} b_1 \\\\ b_2 \\ \end{bmatrix} \quad = \quad a_1b_1 + a_2b_2 \quad = \quad \vec {a}^T \vec b \quad a ⋅ b = ⎣ ⎢ ⎡ a 1 a 2 ⎦ ⎥ ⎤ ∙ ⎣ ⎢ ⎡ b 1 b 2 ⎦ ⎥ ⎤ = a 1 b 1 + a 2 b 2 = a T b
\quad
\quad
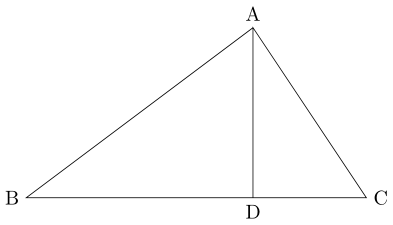
제 2 코사인 법칙 (증명)A B ‾ = c , A C ‾ = b , B C ‾ = a \overline{AB} = c, \quad \overline{AC} = b, \quad\overline{BC} = a \quad A B = c , A C = b , B C = a \quad A D ‾ = b sin C , C D ‾ = b cos C \overline{AD} = b\sin C, \quad \overline{CD} = b\cos C \quad A D = b sin C , C D = b cos C \quad B D ‾ = B C ‾ − C D ‾ \quad\overline{BD} = \overline{BC}-\overline{CD} \quad B D = B C − C D B D ‾ = a − b cos C \quad\overline{BD} = a-b\cos C\quad B D = a − b cos C \quad A B ‾ 2 \quad\overline{AB}^2 \quad A B 2 \quad A B ‾ 2 = c 2 = B D ‾ 2 + A D ‾ 2 \overline{AB}^2 = c^2 = \overline{BD}^2+ \overline{AD}^2 A B 2 = c 2 = B D 2 + A D 2 \quad = ( a − b cos C ) 2 + ( b sin C ) 2 \quad\quad\,= (a-b\cos C)^2 + (b\sin C)^2 = ( a − b cos C ) 2 + ( b sin C ) 2 \quad = a 2 − 2 a b cos C + b 2 cos C 2 + b 2 sin C 2 \quad\quad\,= a^2-2ab\cos C + b^2{\cos C}^2 + b^2{\sin C}^2 = a 2 − 2 a b cos C + b 2 cos C 2 + b 2 sin C 2 \quad = a 2 + b 2 − 2 a b cos C \quad\quad\,= a^2 + b^2 -2ab\cos C = a 2 + b 2 − 2 a b cos C \quad \quad ∴ c 2 = a 2 + b 2 − 2 a b cos C \therefore\,c^2 = a^2 + b^2 -2ab\cos{C} ∴ c 2 = a 2 + b 2 − 2 a b cos C \quad
이를 벡터에 적용해보자.
벡터의 내적 ( 1 ) ∣ a ⃗ − b ⃗ ∣ 2 = ∣ a ⃗ ∣ 2 + ∣ b ⃗ ∣ 2 − 2 ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos θ \quad(1)\quad |\vec{a}-\vec{b}|^2=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos{\theta}\quad ( 1 ) ∣ a − b ∣ 2 = ∣ a ∣ 2 + ∣ b ∣ 2 − 2 ∣ a ∣ ∣ b ∣ cos θ \quad ( 2 ) ∣ a ⃗ − b ⃗ ∣ 2 = ∣ a ⃗ ∣ 2 − 2 a ⃗ ⋅ b ⃗ + ∣ b ⃗ ∣ 2 \quad(2)\quad|\vec{a}-\vec{b}|^2 = |\vec{a}|^2 -2\vec{a}\cdot\vec{b} + |\vec{b}|^2 \quad ( 2 ) ∣ a − b ∣ 2 = ∣ a ∣ 2 − 2 a ⋅ b + ∣ b ∣ 2 \quad ∴ a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos θ \quad \therefore \;\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos{\theta} ∴ a ⋅ b = ∣ a ∣ ∣ b ∣ cos θ \quad \quad
두 벡터를 내적한 값은 θ \theta θ θ \theta θ 9 0 ∘ 90^\circ\; 9 0 ∘ → \rightarrow →
\quad 코사인 유사도 \quad cos θ = a ⃗ ⋅ b ⃗ ∣ a ⃗ ∣ ∣ b ⃗ ∣ \quad \cos\theta = \displaystyle\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|} cos θ = ∣ a ∣ ∣ b ∣ a ⋅ b \quad 9 0 ∘ 90^\circ 9 0 ∘
\; \; \;
참고
∣ x ⃗ ∣ |\vec{x}| ∣ x ∣ L 2 L_2 L 2 = x 1 2 + x 2 2 =\displaystyle\sqrt{{x_1}^2 + {x_2}^2} = x 1 2 + x 2 2 \quad ∣ x ⃗ ∣ 1 |\vec{x}|_1 ∣ x ∣ 1 L 1 L_1 L 1 = ∣ x 1 ∣ + ∣ x 2 ∣ = \displaystyle\left| {x_1} \right| + \left| {x_2} \right| = ∣ x 1 ∣ + ∣ x 2 ∣