Prefix Sum

누적 합(Prefix Sum)

누적 합 알고리즘은 연속된 구간의 합을 빠르게 구할 수 있게 해준다. 이 알고리즘을 알아두면 for문 한 차원을 줄일 수 있어서 시간 제한에서 안걸릴 수 있다. 전에 내 블로그 포스터 중 계수 정렬의 핵심 개념도 누적 합 알고리즘을 사용한 것이다. 가장 핵심 개념은 아래와 같다.

• 주어진 배열의 각 위치까지의 합을 미리 계산해 저장해 둔다.
• 나중에 특정 구간의 합을 O(1) 시간에 빠르게 구할 수 있다

예시 코드를 살펴보면 아래와 같다.

아래는 일반적인 합 계산하는 식이다.

int sum = 0;
for (int i = 2; i <= 5; i++) sum += arr[i];

아래는 누적합 배열로 만들어두고 구간 합 계산을 해주는 코드다.

int[] prefix = new int[arr.length + 1];  // 길이는 1 더 길게
for (int i = 0; i < arr.length; i++)  prefix[i + 1] = prefix[i] + arr[i];
int sum = prefix[6] - prefix[2]; // 2~5까지의 합

이렇게 보면 왜 for문을 줄일 수 있는지 모르겠지만 아래 예시 문제를 보면서 이해하면 쉽다.

예시 문제: 프로그래머스 lv2. 연속 부분 수열 합의 개수

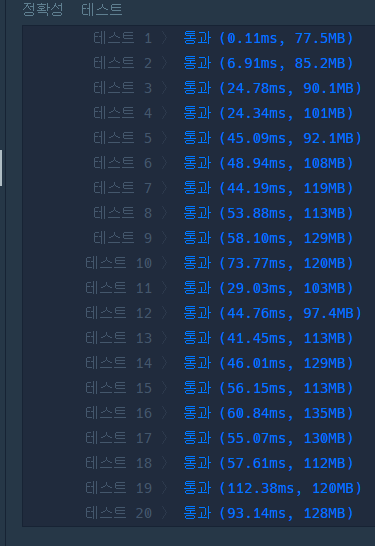
모든 경우의 수 3중 for문

import java.util.Set;
import java.util.HashSet;
class Solution {
    public int solution(int[] elements) {
        Set<Integer> set = new HashSet<>();
        int temp=0;
        int arrLen=elements.length;
        
        for(int i=0; i<arrLen; i++){
            for(int j=1; j<arrLen; j++){
                temp=0;
                for(int k=0; k<j; k++){
                    temp+=elements[(i + k) % arrLen];
                }
                set.add(temp);
            }   
        }
        
        temp=0;
        
        for(int i=0; i<arrLen; i++) temp+=elements[i];
        set.add(temp);
        
        return set.size();
    }
}

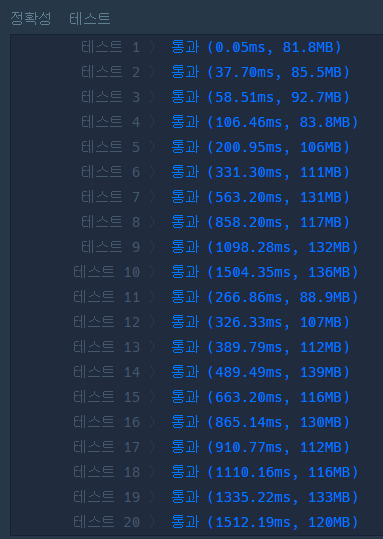
누적합 사용 풀이

import java.util.Set;
import java.util.HashSet;
class Solution {
    public int solution(int[] elements) {
        int n = elements.length;
        int[] prefixArr = new int[2*n+1];
        Set<Integer> sumSet = new HashSet<>();
        
        for(int i=1; i<n*2+1; i++) prefixArr[i] = prefixArr[i-1] + elements[(i-1)%n];
        
        for(int len=1; len<=n; len++){
            for(int i=0; i<n; i++){
                sumSet.add(prefixArr[i+len]-prefixArr[i]);
            }
        }
        
        return sumSet.size();
    }
}