계수 정렬(Counting Sort)

계수 정렬에 대해서 알아보자.
기존에 Arrays.sort()만 거의 사용했던 것 같다.
Arrays.sort()는 고성능 퀵소트를 사용한다고 알고있다. 그래서 시간복잡도는 아래와 같다.
평균 시간복잡도: O(n log n)
퀵소트도 충분히 빠른 정렬이긴 하지만 0을 포함한 양의 정수의 정렬은 n+k로 훨씬 단축할 수 있는 방법이 있어서 배워두면 좋을 것 같아서 정리했다.
심지어 어떤 기업 코테에서는 정렬을 라이브러리로 쓰면 면접에서 다시 구현해보라 하거나 못쓰게 제한하는 기업도 있다고 들었다.

🧮 1. 계수 정렬 (Counting Sort)
✅ 개념
원소의 값 자체를 인덱스로 사용해서 카운트를 세는 방식의 정렬.

정수(또는 양의 정수) 데이터를 다룰 때 매우 효율적.

중복되는 값도 처리 가능.

✅ 동작 방식 예시 (정수 배열 A: [4, 2, 2, 8, 3, 3, 1])

1. 해당 정수 배열의 최댓값(8)을 기준으로 카운트 배열 생성 (B: count[0..8])

   • 배열 크기가 9(최댓값+1)이며, 각 값은 0이 들어가있는 배열 생성.

2. 배열 A를 for문 돌면서 각각의 숫자가 나올때마다 B배열에 누적. ex) A의 첫번째 수가 4이면 B배열의 4번째 인덱스에 1을 더함.

   • 위에서 생성한 배열 B에 각 숫자별로 등장 횟수 기록 → [0,1,2,2,1,0,0,0,1]

3. 배열 A크기와 같은 결과 배열 C를 생성.

4. B배열을 돌면서 B[i]의 값이 0이될때까지 C에 i를 삽입.

정렬 완료: [1,2,2,3,3,4,8]

✅ 시간/공간 복잡도
시간: O(n + k) (n: 데이터 수, k: 데이터 범위)

공간: O(k)

단점: 데이터 범위(k)가 너무 크면 메모리 낭비 심함

✅ 특징
음수 불가, 실수 불가

안정 정렬

범위가 작고 정수일 때 최강 성능

코드로 직접 짜보고 성능평가 해보자. (코딩테스트 lv2, 최솟값 만들기)

1. java util의 Array 패키지의 정렬 사용

import java.util.*;
class Solution
{
    public int solution(int []A, int []B)
    {
        int answer = 0;

        Arrays.sort(A);
        Arrays.sort(B);
        
        for(int i=0; i<A.length; i++){
            answer+= A[i]*B[B.length-i-1];
        }

        return answer;
    }
}

2. 계수 정렬 사용

   • 2-a: 자바에서 배열로 최댓값 찾으려면 Collection이나 Arrays뭐 써서 해야하는데 그냥 나는 구현하는 편이다.

   private int findMax(int[] arr){
       int max=Integer.MIN_VALUE;
       
       for(int num : arr){
           if(num>max) max=num;
       }
       
       return max;
   }

   • 2-b: 계수 정렬 코딩(2-a에서 구현한 최댓값 찾는 함수 활용)

   private int[] countingSort(int[] A){
       int max=findMax(A);
       int[] B = new int[max+1];
       
       for(int num : A){
           B[num] ++;
       }
       
       int[] C = new int[A.length];
       int index = 0;
       
       for(int i=0; i<B.length; i++){
           while(B[i]>0){
               C[index++] = i;
               B[i]--;
           }
       }
   
       return C;
   }

   • 2-c: 기존 코드 수정, 배열 A, B만 기존 Arrays 패키지 쓰던거 계수정렬 함수로 바꿔줬다.

   public int solution(int []A, int []B)
   {
       int answer = 0;
   
       A = countingSort(A);
       B = countingSort(B);
       
       for(int i=0; i<A.length; i++){
           answer+= A[i]*B[B.length-i-1];
       }
   
       return answer;
   }

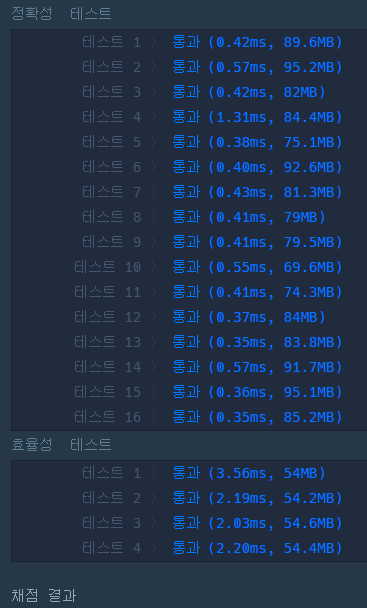
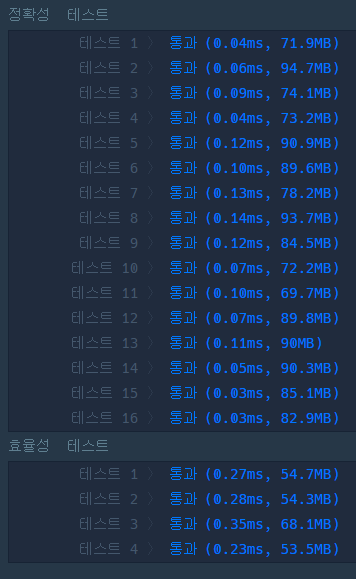
결과 비교
(1)Arrays.sort()

(2) Counting sort - 계수 정렬