4wis-4wid 차량제어

K - ROAD·2025년 12월 30일

4wid 4wis 4륜구동 4륜제어 MPC kroad6기 논문리뷰 제어 조향

안녕하세요, K-road의 박성민입니다.
저는 현재 학부연구생으로 참여하고 있는 과수원 환경 4WIS-4WID 플랫폼제어에 대해 다뤄보고자 합니다.

프로젝트 진행 중 제어 알고리즘의 뼈대를 이해하는 데 큰 도움이 된 논문을 리뷰하도록 하겠습니다.

본 리뷰는 제가 직접 작성한 논문이 아니라, 학부연구생 활동을 진행하는데 참고하고 있는 '과수원 환경 4WIS-4WID 자율주행 플랫폼을 위한 계층적 모션 제어기 설계' (이요셉 외, 한국자동차공학회) 를 바탕으로 작성했습니다. 흔한 비이시클 모델이 아닌 4WIS-4WID 제어의 기초부터 고도의 최적화 기법까지 다루고 있어, 관련 분야에 입문하는 연구원들에게 추천합니다.

4WIS-4WID란?

4WIS (Four-Wheel Independent Steering): 네 바퀴를 각각 독립적으로 조향할 수 있는 시스템입니다. 단순 네 바퀴 조향을 하는 4WD가 아닌 각 바퀴가 모두 독립적인 4WID로써 기존 플랫폼과 같이 2WS 차량이 구현하지 못하는 '크랩 주행(측면 이동)'이나 '제자리 회전'이 가능합니다.
4WID (Four-Wheel Independent Drive): 각 바퀴에 독립적인 구동 모터가 장착되어 속도와 토크를 개별적으로 제어할 수 있는 특수 기동 플랫폼입니다.
과수원 환경의 특수성: 과수원은 통로가 매우 협소하고 복잡하며, 불규칙한 경계면과 정적 장애물이 존재합니다. 따라서 일반적인 조향 시스템으로는 기동에 한계가 있으며, 4WIS-4WID 플랫폼의 높은 기동성이 필수적입니다.

기존 4WIS-4WID제어의 문제점

거동의 불연속성과 누적 오차 발생

기존 연구들은 주행 상황에 따라 애커만 조향, 크랩 조향, 제자리 회전 등 특정 모드를 미리 정의하고 이를 스위칭하는 방식을 사용해 왔습니다. 하지만 이 방식은 다음과 같은 부작용을 낳습니다.

조향각의 급격한 변화: 주행 중 모드가 바뀌는 순간, 스위치와 같이 각 바퀴의 조향 각도 지령이 순식간에 큰 폭으로 변하게 됩니다.
불연속적 주행: 이러한 급격한 변화는 차량 거동의 불연속성을 유발하며, 이는 곧 차량 방향 각도의 누적 오차로 이어집니다. 좁은 과수원 통로에서 이러한 미세한 오차는 나무와의 충돌로 이어질 수 있는 위험 요소가 되기도 합니다.

물리적 충격과 진동

모드 전환은 단순히 소프트웨어적인 숫자 변화에 그치지 않고, 실제 기계 시스템에 물리적 부담을 줍니다.

전환 충격: 모드가 바뀌는 찰나에 발생하는 급격한 토크 변화나 조향 모터의 움직임은 차량 전체에 충격이나 진동을 발생시킬 수 있습니다.
추가 설계의 필요성: 이를 완화하기 위해 조향각 궤적을 B-스플라인 곡선으로 부드럽게 설계하거나, 강인 제어기를 추가로 도입하는 등 제어기 구조가 불필요하게 비대해지는 결과를 초래합니다. 즉, 문제를 해결하기 위해 또 다른 복잡한 해결책을 덧붙여야 하는 구조적 한계가 존재합니다.

제어 알고리즘의 연산 복잡도 급증

모드를 자동으로 선택하고 최적화하려는 시도들은 필연적으로 계산량의 한계에 부딪힙니다.

혼합 정수 최적화 문제: 주행 상황에 맞춰 최적의 모드를 선택하기 위해 혼합 정수 모델 예측 제어(MIQP-MPC) 등을 도입할 경우, 매 제어 주기마다 연속적이지 않고 이산적인 정수 변수를 처리해야 하여, MPC의 연산 부담이 극도로 커지게 됩니다.
다목적 최적화의 한계: 여러 모드 사이의 동적 전환을 실시간으로 계산하고 다목적 유전 알고리즘 등을 적용하면 알고리즘의 복잡도가 기하급수적으로 높아져 실시간 제어 성능을 보장하기 어려워집니다.

계층적 최적 제어 알고리즘

본 논문의 코어인 제어기는 상위 및 하위 계층으로 나누어 제어를 수행합니다.

상위제어기

경로 추종 MPC

상위 계층은 차량이 기준 경로를 정확히 따라갈 수 있도록 차체 전체의 최적 속도 명령을 생성하는 역할을 합니다.

• 제어 목표: 차량의 상태 오차(종방향 오차 $e_x$ , 횡방향 오차 $e_y$ , 헤딩 오차 $e_\phi$ )를 최소화하는 차체 레퍼런스 벡터 $v_{ref} = [v_x, v_y, \omega]$ 를 도출합니다. 여기서 차량 레퍼런스 벡터는 차체의 종,횡방향 속도와 요레이트를 의미합니다.

• 모델 예측 제어(MPC) 적용: 비선형 목적함수를 간단하게 구현하기 위해 MPC를 사용합니다. 특히 실시간 연산 속도를 확보하기 위해 단일 스텝(One-step) 동안의 거동만 예측하도록 설계했습니다.

• 예측 모델: 시간 이산화된 상태 공간 방정식을 활용합니다.

◦ 상태 벡터: $x(k) = [e_x, e_y, e_\phi]$

◦ 입력 벡터: $u(k) = [v_x, v_y, \omega]$

◦ 시스템 행렬 A와 입력 행렬 B는 항등 행렬에 샘플링 시간 Delta t를 곱한 형태로 구성되어 계산 효율을 극대화합니다.

◦ 상태공간방정식은 다음과 같다.

$x(k+1) = Ax(k) + Bu(k)$

$A = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, B = \begin{bmatrix} \Delta t & 0 & 0 \\ 0 & \Delta t & 0 \\ 0 & 0 & \Delta t \end{bmatrix}$

하위제어기

상위 계층에서 도출된 차체 속도 명령은 하위 계층에서 각 바퀴의 조향각과 구동 속도로 실시간 변환됩니다.

• 기하학적 변환: 차체 속도( $v_x$ , $v_y$ , $\omega$ )와 각 바퀴의 조향각 및 구동 속도 사이의 단순한 기하학적 관계식을 이용합니다.

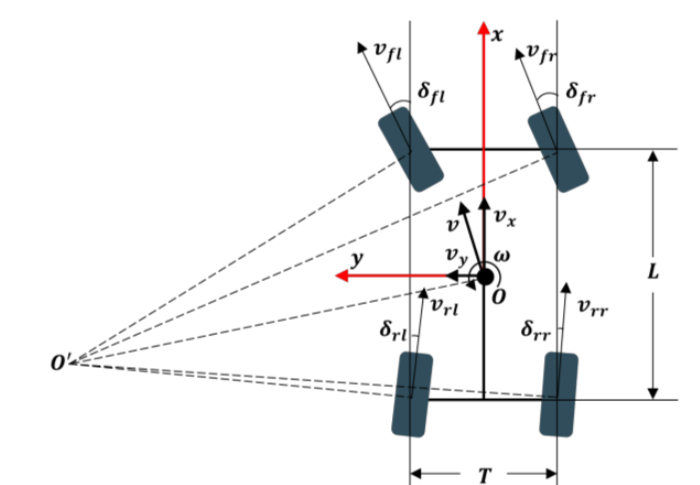
$\delta_{ij} = \tan^{-1}\left(\frac{v_y + s_i \omega \frac{L}{2}}{v_x + t_j \omega \frac{T}{2}}\right)$

$v_{ij} = v_x \cos\delta_{ij} + v_y \sin\delta_{ij} + s_i \omega \frac{L}{2} \sin\delta_{ij} + t_j \omega \frac{T}{2} \cos\delta_{ij}$

통합 기동 구현: 이 변환식을 통해 별도의 모드 전환 없이도 다음과 같은 기동이 가능해집니다.

• 크랩 주행: 요레이트가 없고 $v_x$ , $v_y$ 성분이 존재하면 모든 바퀴가 같은 각도로 조향됩니다.

• 제자리 회전: $v_x=0$ , $v_y=0$ 이고 요레이트성분만 존재하면 바퀴가 회전 중심을 향하도록 정렬되고 제자리 회전이 가능해집니다.

• 복합 기동: 임의의 병진 및 회전 운동 조합을 실시간으로 구현할 수 있습니다.

연성 제약(Soft Constraint)을 통한 시스템 안정화

본 논문의 핵심 기여 중 하나는 액추에이터의 물리적 한계를 처리하는 방식입니다.

• 경성 제약(Hard Constraint)의 문제: 조향각이나 속도를 강제로 제한하면 제약 충돌 시 최적해를 찾지 못해 제어가 중단될 위험이 있습니다.

• 연성 제약 도입: MPC의 비용 함수에 제약 위반에 대한 페널티 항을 포함하여 항상 최적해를 도출할 수 있도록 설계합니다.

$J = x(k+1)^T Q x(k+1) + u(k)^T R u(k) + c(k)^T W c(k)$

• 페널티 벡터 $c(k)$ : 각 바퀴의 조향각과 속도가 임계값을 초과할 때만 초과분을 비용으로 부과합니다.

이 방식을 통해 하드웨어의 한계 내에서 추종 오차를 최소화하는 부드러운 제어 출력을 얻을 수 있습니다.

성능 검증 및 결론

MATLAB 및 CarMaker 시뮬레이션을 통해 제안된 제어기의 우수성을 확인한 결과는 다음과 같습니다.

추종 정밀도: 기존 N-스텝 선형 MPC와 비교했을 때, 10km/h 주행 조건에서 평균 오차를 50% 이상 감소시켰습니다.

실시간성: 12세대 i9 CPU 기준 평균 연산 시간은 약 0.61ms로, 실제 차량에 적용하기 충분한 실시간 성능을 보였습니다.

특수 기동 구현
◦ 제자리 회전(Zero-turn): 차량의 진행 방향과 반대로 정렬된 상황에서 횡방향 이탈 없이 정확히 180도 회전에 성공했다.
◦ 평행 이동(Lateral Shift): 경로와 4m 떨어진 위치에서 차체 방향을 유지한 채 별도의 요레이트 없이 측면으로 이동하여 안정적으로 합류했다

과수원 환경에서 4륜 조향 및 4륜 구동 플랫폼에 관한 논문을 쭉 리뷰해봤는데 단순히 조향 모드를 나누는 막노동식 코딩에서 벗어나, MPC와 연성 제약이라는 수학적 도구로 4WIS의 잠재력을 100% 끌어올린 논문이라고 생각합니다.

LQR제어와 비슷한 MPC이지만 제약을 추가한 비용함수를 넣어 최근 떠오르고 있는 현대 제어인 MPC에 대해 잘 보여주고 있는 것 같습니다.

특히, 제약 조건을 비용 함수로 녹여낸 부분은 'Solver Crash'등과 같이 실차 제어 시 발생할 수 있는 문제점들을 예방할 수 있는 아주 실무적인 접근으로 보입니다.

K - ROAD

한국기술교육대학교 자율주행연구회 K-ROAD의 기술블로그 입니다.