MPC 개요

K - ROAD·2025년 3월 7일
MPCkroad5기알고리즘자율주행제어

안녕하세요, KROAD5기 원윤재입니다. 차세대 차량 제어로 대두되는 MPC에 대해 간단한 소개를 드리고자 합니다.

MPC (Model Predictive Control) 소개

  • Optimal Control의 한 방법

Optimal Control이란?

  • Optimal Control Algorithm이라고도 하며, 한국말로는 최적 제어입니다.

  • 차량이 어느 한 기점, 종점의 위치와 통행 시간이 주어졌을 경우 연료 효율을 최적화 하는 차량 궤적을 찾는 알고리즘.

  • OCA의 수식을 보면 , 최고/최저 속도 및 가속도를 제한해놓고, 연료 효율과 직결된 가속도를 찾는 형식입니다.

  • 아래 그림을 보면 신호의 변경이 있고(좌), 없는(우) 상황에서 OCA기반의 주행은 아닌 주행보다 연비의 입장에서 효율적으로 동작한다는 점을 알 수 있습니다.

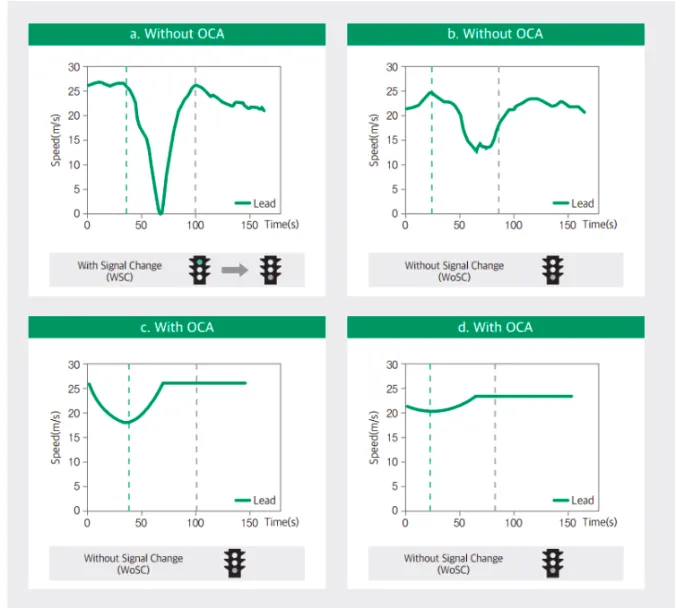
  • 다시 MPC로 돌아와서, 결국 MPC의 목적은 주어진 상황에서 최적화된 제어 명령을 생성하는 것입니다.

  • 방법

    • 속도 및 가속도와 같은 dynamics와 주변 환경 조건을 cost function으로 넣어 상황에 맞는 조건 결과 도출
    • cost function : 일종의 error(오차값), 내가 만든 모델이 실제 값과 얼마나 다른지를 측정하는 수단으로, 값이 클수록 해당 모델의 정확도가 낮다는 의미

MPC의 간단 개요

  • k-1일 때의 상태변수를 가지고 논다.

  1. k-1을 이용해 k-step(현재) 부터 몇 수 앞 ( ex) k+5 )까지의 제어 명령을 미리 계획합니다.

  2. 계획한 명령을 출력하고 이번엔 k-step(현재)의 상태변수를 불러와 feedback합니다.

  3. (1) 과정에서 k-1에서 계획한 k-step의 제어 명령과 (2)에서 불러온 k-step의 응답을 비교해서 평가합니다.

  4. 이에 따라 위에 언급한 cost-function을 update해 다시 k+1과 k+6까지의 명령을 계획합니다.

    즉, ‘계획 —> 평가 —> 계획 —> 평가 —> 계획 —> 평가’ 를 반복하면서 발견한 constraint(제약조건)을 가지고 최적화된 제어 입력을 생성합니다.

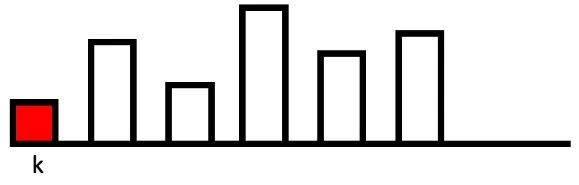    K -1의 상태변수를 가지고 K-step에서부터 예측된 제어 명령

위 그림은 k-1 에서의 상태변수를 가지고 k step에서 출력해야할 제어 명령을 미리 예측한 것입니다.

위 그림에서는 k+5 까지 했습니다. 이제 예측한 제어명령을 출력하고, 이 명령과 k에서의 response를 비교합니다. 이 때 비교된 결과에 따라 다시 k step을 우리가 아는 k-1로 놓고, k-step을 예측하는 것입니다

실제 k-1에서 예측한 것과, k에서 response를 보고 다시 예측한 것과 차이가 발생하는데, 그게 바로 아래 그림에서 점선에 해당하는 부분들입니다.

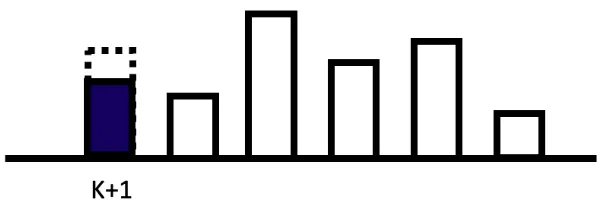다시 출력과 응답을 비교해서 현재 상태에서 최적화된 제어명령을 출력합니다.
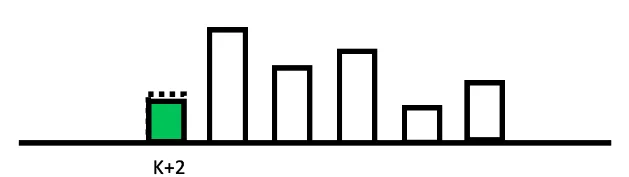결국 아래 그림처럼, 최초의 k-1에서 생성되었던 제어 명령과는 다른 각 step에서 최적화된 명령들이 출력됩니다.

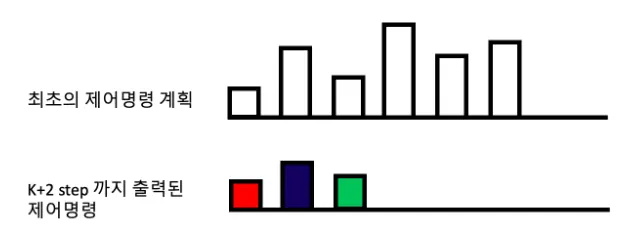
MPC MODELING

현재 Step의 상태변수를 가지고 다음 Step을 ‘예측’해 ‘출력’하기 때문에, 시스템 dynamics의 모델링이 필요합니다.

기초 모델링은 주로 선형 시불변 시스템(Continous-time state-space model)을 기반으로 이루어지지만, MPC는 이산 시간에서 구현이 되기 때문에 모델링을 이산 시간(Discrete-time state-space model)기반 모델링을 해주어야 합니다.

  • Continous-time (연속 시간) vs Discrete-time (이산시간)

    • Continous-time: 시스템의 입력과 출력 모두 연속적인 시간에서 표현되는 연속시간 시스템

      • 0초와 1초 사이에 존재하는 무한한 순간들을 고려
      • y(t) = T[ x(t) ]

    • Discrete-time: 입력과 출력이 일정 시점 (이산적인 시간)에서만 정의되는 이산시간 시스템

      • 0초, 1초 , 2초 와 같이 간격이 존재하는 , 0초와 1초 사이에 존재하는 무한한 시간은 고려하지 않는 것.
      • 이산 시점에서 입력신호 x[n]을 출력신호 y[n]로 연산하는 시스템
      • y[n] = T[ x(n) ]

공부를 하면서도, 연속시간과 이산시간의 차이점은 알겠으나, 이산시간 시스템에서 모델링을 하는 이유에 대해서는 직접적으로 와닿지 않아 더 찾아보았습니다.

  • Discrete-time state-space Modeling을 하는 이유

    • 앞서 언급했 듯, 이산시간에서는 시스템의 상태 및 입력이 이산화됩니다. 간격이 명확하게 존재하기 때문에, 시스템의 제어에 필요한 정보를 주기적으로 수집하고 입력을 조절하기에 용이합니다.

    • MPC는 미래의 시스템 동작을 예측하여 입력을 넣기 때문에, 예측 프레임워크에서 이산시간 모델의 사용이 상태 및 출력을 예측하는 과정에서 단순하고 효율적입니다.

MODELING

MPC 기본 모델링에서 가장 중요한 점은, 상태방정식에서 상태변수가 x 가 아닌 상태변수의 변화량, 즉 Δx를 사용하는 것입니다.

그 이유는, 상태변수의 변화량을 사용하면 시스템의 다음 상태를 현재 상태와 입력에 기반하여 직접적으로 예측할 수 있기 때문이고 이는 시스템 동작의 미래 예측을 훨씬 더 정확하고 효율적으로 설계 할 수 있습니다.

% DC_Motor_MPC.m
% DC_motor Characteristics
R = 8.4; %resistence 
kt = 0.042; %current torque
km = 0.042; %back-emp constant
L = 1.16; %Inductance
J = 2.09*10^-5; %inertia
B = 0.0001; %Viscous coefficient

%Continuous-time model
A = [0 1 0; 0 -B/J kt/J; 0 -km/L -R/L];
B = [0; 0; 1/L];
C = [1 0 0];
D = zeros(1,1);
dt = 1;
[Ad, Bd, Cd, Dd] = c2dm(A,B,C,D,dt);

%MPC gain
N_sim = 100;
Np = 10; %predictive states
Nc = 4;  %future output

[Phi, Phi_F, Phi_R, Ae, Be, Ce] = mpcgain(Ad, Bd, Cd, Nc, Np);
[n, n_in] = size(Be);
xm = [0;0;0];
xf = zeros(n,1);

r = 10*ones(N_sim,1) %constant_reference
u = 0;
y = 0; 
R_bar = 10000*eye(Nc,Nc);

for k = 1 : N_sim;
    DeltaU = inv(Phi'*Phi + R_bar)*(Phi_R*r(k)-Phi_F*xf);
    deltau = DeltaU(1,1);
    u = u+deltau
    u1(k) = u;
    y1(k) = y;
    xm_old = xm;
    xm=Ad*xm+Bd*u
    y = Cd*xm;
    xf = [xm-xm_old;y];
end

k = 0:(N_sim-1);
figure
subplot(211)
plot(k,r,'k','LineWidth', 2);
hold on
plot(k,y1,'r--','LineWidth', 2);
grid on;
legend('ref', 'output');
ylim([-1 12]);
subplot(212)
plot(k,u1,'b','LineWidth', 2);
legend('control input');
ylim([-0.1 1])

%mpcgain.m
function [Phi, Phi_F, Phi_R, Ae, Be, Ce] = mpcgain(Ad, Bd, Cd, Nc, Np);
    
    %Ae, Be, Ce = Augmented Discrete-time model of Ad,Bd,Cd matrix
    %Ad, Bd, Cd is from c2dm of A, B, C    
    
    %Continuous to discrete time model conversion example
%     A = [0 1 0; 3 0 1; 0 1 0];
%     B = [1; 1; 3];
%     C = [0 1 0];
%     D = zeros(1,1);
%     dt = 1;
%     [Ad, Bd, Cd, Dd] = c2dm(A,B,C,D,dt);
    
    %discrete to autmented discrete time model conversion
    % Ae = [ Ad 0; CdAd 1]
    % Be = [ Bd; CdBd]
    % Ce = [ 0 0 ... 0 (# of states)   1 1 ... 1 (# of outputs) ]
    [N_outputs, N_states] = size(Cd);
    [N_states, N_inputs] = size(Bd);
    Ae = eye(N_states+N_outputs, N_states+N_outputs); 
    Ae(1:N_states, 1:N_states) = Ad;
    Ae(N_states+1:N_states+N_outputs, 1:N_states) = Cd*Ad;
    Be = zeros(N_states+N_outputs, N_inputs);
    Be(1:N_states,:) = Bd;
    Be(N_states+1:N_states+N_outputs,:) = Cd*Bd;
    Ce = zeros(N_outputs, N_states+N_outputs);
    Ce(:, N_states+1:N_states+N_outputs) = eye(N_outputs, N_outputs);
    
    h(1, :) = Ce;
    F(1, :) = Ce*Ae;
    
    for k = 2: Np
        h(k,:) = h(k-1, :)*Ae;
        F(k,:) = F(k-1,:)*Ae;
    end
    
    v = h*Be;
    Phi = zeros(Np,Nc);  
    Phi(:,1) = v; % first column of Phi
    for i = 2 : Nc
        Phi(:,i) = [zeros(i-1,1); v(1:Np-i+1,1)];
%       Phi = Toeplitz (diagonal-constant) matrix
    end
    
    Rs = ones(Np,1);    
    Phi_F = Phi'*F;
    Phi_R = Phi'*Rs;
end

이상, MPC에 대한 간단한 소개를 마치겠습니다.

곡률이 큰 주행에서, Stanley, Kanayama 방식보다 더욱 효과적이라고 판단되어, 협로 미션에 적용해보고자 연구를 진행하고 있습니다.

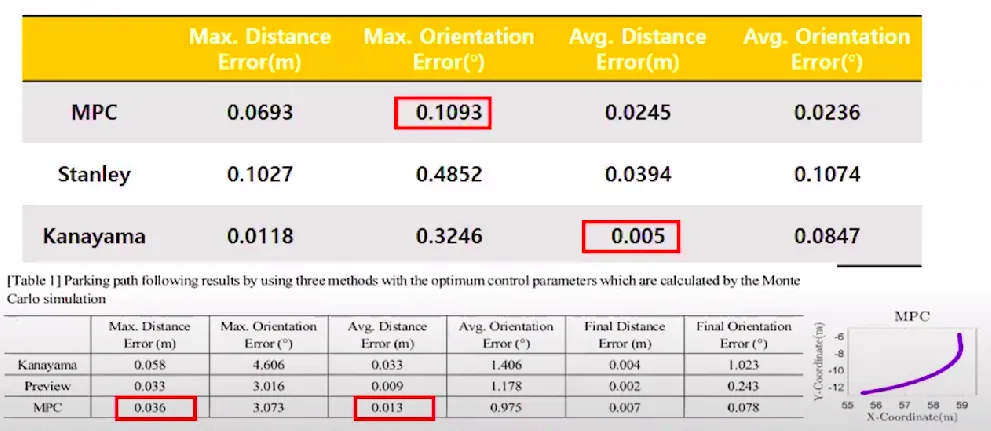
Reference

자율 주차 시스템을 위한 주차 경로 추종 방법의 비교 연구

[ 조향제어 / 모터제어 ] https://lsoovmee-rhino.tistory.com/entry/8

profile
K - ROAD
한국기술교육대학교 자율주행연구회 K-ROAD의 기술블로그 입니다.
이전 포스트

C-ITS 통신

다음 포스트

DWA

0개의 댓글