mAP란?

Krrong·2022년 5월 5일

인공지능

목록 보기

1/1

📌 Intro

좋은 기회로 학교에서 학부 연구생을 하게 되었고, 현재 faster RCNN에 대해 공부하고 있다. AI분야는 아는 것이 많이 없어서 공부한 내용을 정리하며 조금씩 쌓아가려고 한다.

mAP는 mean Average Precision이고, 컴퓨터 비전에서 객체 검출 알고리즘의 성능을 평가하는 지표로 사용한다. (mAP로 구글에 검색하면 지도만 잔뜩 뜬다..)

mAP를 이해하기 위해서 몇 가지 사전 지식이 필요하기 때문에 그것부터 알아보도록 하자.

📌 True? False?

실제 세상의 사람을 컴퓨터는 사람으로 판단할 수도 있고, 사람이 아닌 다른 객체로 판단할 수 있고, 객체로 판단하지 않을 수 있고, 실제로 사람이 아닌 것을 사람으로 판단할 수 있는 네 가지 경우가 있다.

말장난 같아 보이니 조금 더 자세히 알아보자.

	Positive	Negetive
Positive	True Positive	False Negative
Negative	False Positive	True Negative

True Positive : 실제로 사람인 것을 컴퓨터가 사람이라고 검출한 것(올바른 검출이라고 생각할 수 있다.)
False Positive : 실제로 사람이 아닌것을 컴퓨터가 사람이라고 검출한 것(틀린 검출이라고 생각할 수 있다.)
False Negative : 사람을 사람이 아니라고 판단하는 것
True Negative : 사람이 아닌 것을 사람이 아니라고 판단하는 것

모든 내용이 중요하지만 mAP를 이해하기 위해 사용하는 개념은 강조 표시된 것들이다.(TP, FP, FN)

📌 Precision

Precision은 정확도를 말하고 검출한 결과들 중 올바르게 검출한 비율을 의미한다.
나는 수식을 싫어하지만 그래도 수식으로 나타내보면 아래와 같다.

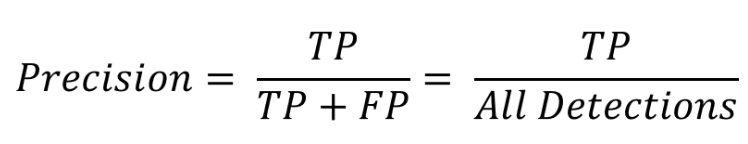
컴퓨터가 사람이 10명이라고 검출했을 경우 7명이 실제로 사람이라면 Precision은 70%가 되는 것이다.

📌 Recall

Recall은 재현율을 말하고 실제로 옳은 것들 중 옳다고 검출한 비율을 의미한다.
역시 수식으로 표현하면 아래와 같이 나타낼 수 있다.

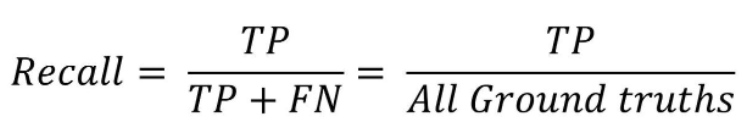
사람이 10명이 있고 이 중 6명을 사람이라고 검출하면 Recall은 60%가 되는 것이다.

📌 P-R 곡선

PR곡선은 Confidence threshold값에 따른 Precision과 Recall의 변화를 그래프로 표현한 것이다. 여기서 Confidence는 검출한 객체에 대해 얼마만큼의 정확도를 가지고 있는지를 의미한다.

검출된 모든 객체를 Confidence를 기준으로 내림차순으로 정렬한다. 그리고 Confidence의 threshold값을 가장 높은 값에서부터 하나씩 낮춰가며 Precision과 Recall을 계산한다.

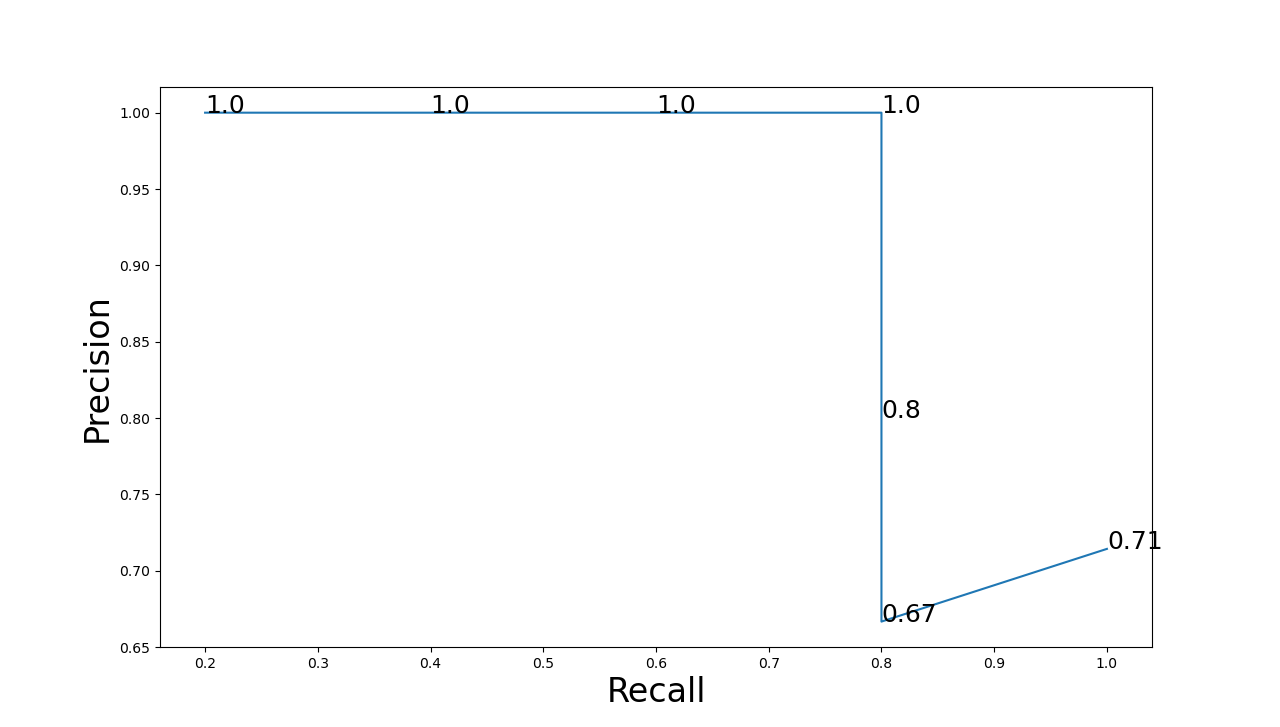
그것을 표로 나타내면 아래와 같다.

Detection	Confidence	TP/FP	누적 TP	누적 FP	Precision	Recall
B	95%	TP	1	0	1/1 = 1	1/15 = 0.067
A	91%	TP	2	0	2/2 = 1	2/15 = 0.133
D	88%	TP	3	0	3/3 = 1	3/15 = 0.2
F	86%	TP	4	0	4/4 = 1	4/15 = 0.267
Q	75%	FP	4	1	4/5 = 0.8	4/15 = 0.267
R	53%	FP	4	2	4/6 = 0.667	4/15 = 0.267
S	40%	TP	5	2	5/7 = 0.714	5/15 = 0.333

같은 객체에 대한 검출만을 계산하고(예를들면 사람만을 검출한 것만 대상) 이 표를 기반으로 Precision과 Recall에 대한 그래프를 그리면 그것이 P-R곡선이 되는 것이다.

위 그래프에 대한 P-R곡선은 아래와 같다.

📌 P-R 곡선 Python 코드

import pandas as pd
import matplotlib.pyplot as plt

def PR(inp1):
    Precision = []
    Recall = []
    P = len(inp1[inp1['label'] == 'TP'])
    N = len(inp1[inp1['label'] == 'FP'])
    
    for i in inp1['probability']:
        tmp_p = data[data['probability'] >= i]
        TP = len(tmp_p[tmp_p['label'] == 'TP'])
        tmp_precision = TP/len(tmp_p)
        tmp_recall = TP/P
        Precision.append(tmp_precision)
        Recall.append(tmp_recall)
    
    return Precision, Recall


index = ['B','A','D','F','Q','R','S']
label = ['TP','TP','TP','TP','FP','FP','TP']
probability = [0.95,0.91,0.88,0.86,0.75,0.53,0.40]

data = pd.DataFrame({'index' : index, 'label':label, 'probability':probability})
print(data)

Precision, Recall = PR(data)

fig = plt.figure()
fig.set_size_inches(15, 15)
plt.plot(Recall, Precision)
plt.xlabel("Recall", fontsize=24)
plt.ylabel("Precision", fontsize=24)
for i in range(len(data['probability'])):
    plt.text(Recall[i], Precision[i], data['probability'][i], fontsize=18)
    
plt.show()

📌 Average Precision (AP)

위에서 살펴본 P-R곡선은 어떤 알고리즘의 성능을 전반적으로 파악하기에는 좋지만 서로 다른 알고리즘의 성능을 정량적으로 비교하기는 어렵다. 그래서 Average Precision이라는 개념이 등장했고, 이는 P-R곡선 그래프 아래쪽의 면적으로 계산한다. 이 값이 높을수록 알고리즘의 성능이 좋다고 판단할 수 있다.
(보통 계산하기 전에 PR곡선을 단조적으로 감소하는 그래프로 변경해준다.)

📌 mean Average Precision (mAP)

객체 클래스가 여러개인 경우 각 클래스별로 Average Precision 값이 나올 것이고, 이것을 모두 더한 뒤 클래스 수로 나눠 얻는 값을 mean Average Precision (mAP)라고 한다.

🚥 참고

[1] https://ctkim.tistory.com/79
[2] https://pbj0812.tistory.com/365

Krrong