
🤔 다이나믹 프로그래밍?
알고리즘 문제풀이를 하다 보면 한번쯤은 이 이상한 태그를 보게 됩니다.
다이나믹 프로그래밍
대체 다이나믹 프로그래밍이 뭘까요?
그리고 이 태그가 붙은 문제는 왜 다들 해결방법이 가지각색인 걸까요?
그것이 알고싶다 다이나믹 프로그래밍
다이나믹 프로그래밍은 알고리즘을 설계하는 방법으로, 큰 문제를 작은 문제로 나누어 작은 문제의 답을 큰 문제에 적용하는 "계획"을 세우는 문제 해결 기법입니다.
다이나믹 프로그래밍은 아래의 조건을 만족할 때 사용할 수 있습니다.
- 최적 부분 구조 (Optimal substructure)
큰 문제를 작은 문제로 분해, 작은 문제의 답을 큰 문제에 사용할 수 있는 경우를 의미합니다.
일종의 분할-정복(Divide and conquer)이기도 합니다. - 중복되는 부분 문제 (Overlapping subproblem)
작은 문제가 반복 풀이되는 경우를 의미합니다.
작은 문제의 답을 큰 문제에 어떻게 적용하느냐가 다이나믹 프로그래밍의 핵심으로, 이 계획을 어떻게 세우냐에 문제 풀이의 성패가 좌우됩니다.
간단한 예시를 보면서 DP가 무엇인지 알아봅시다.
🪆 DP의 훌륭한 예시, 피보나치 수열
재귀로도 해결할 수 있지만...
피보나치 수열은
f(0) = 0
f(1) = 1
f(n) = f(n - 1) + f(n - 2) (n >= 2)
를 만족하는 수의 집합입니다.
이 수열의 n번째 값을 구하는 fibonacci() 함수의 재귀적인 구현은 표현이 명료한 재귀 알고리즘의 예시로 잘 알려져 있습니다.
public int fibonacci(int n) {
if (n < 2)
return n;
return fibonacci(n - 1) + fibonacci(n - 2);
}코드가 필요 이상으로 길어진다는 말을 자주 듣는 Java로도 이렇게 짧고 명료한 코드가 나옵니다.
그런데 이 재귀 알고리즘은 n 이 커질 경우 함수 호출이 지수 스케일로 엄청나게 증가하게 됩니다.
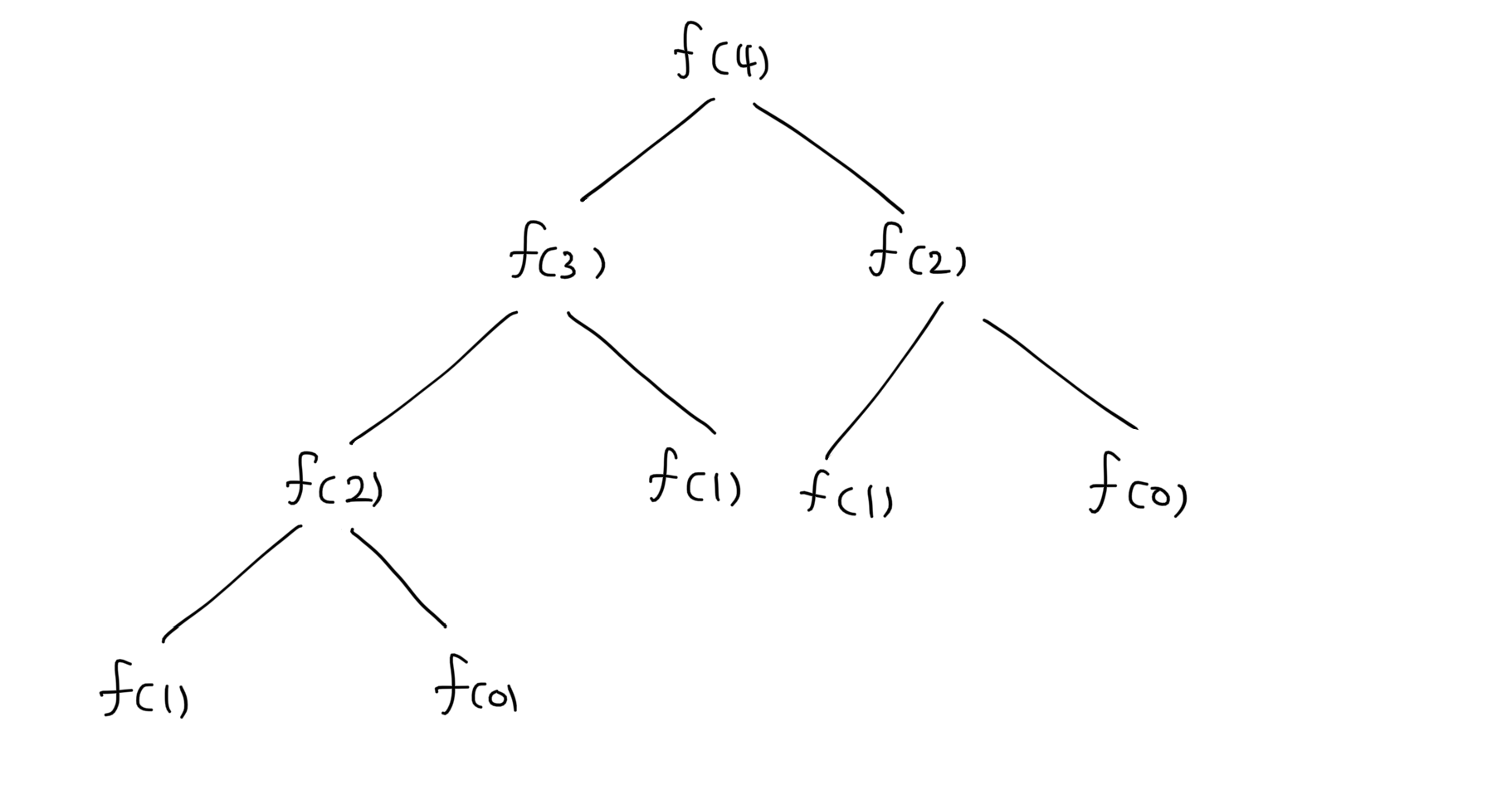
가령 4번째 피보나치 수를 구하는 과정에서의 호출 트리입니다. f(1) 과 f(0) 은 상수를 리턴하지만, 계산이 필요한 f(3), f(2) 에 대해 중복 계산이 발생하고 있습니다.
여기에서 n 이 30만 되어도 약 5억의 호출이 발생하며 호출 스택 공간은 이를 고려해서 설계되지 않았으므로 stack overflow 오류를 발생시킵니다.
스택 공간을 임의로 늘린다 하더라도 수행 시간이 폭증하는 점은 변함이 없기에 우리는 다른 해결 방법을 찾을 필요가 있습니다.
이미 나온 결괏값을 어떻게 활용할까?
앞서 필자는 작은 문제의 답을 큰 문제의 정답에 활용하는 것이 다이나믹 프로그래밍이라 하였습니다.
그러면 피보나치 수를 구할 때 작은 문제와 큰 문제는 각각 무엇일까요?
위의 예시에서처럼 f(4) 를 구한다면 f(3), f(2), f(1), f(0) 이 각각 작은 문제가 됩니다.
따라서, n번째 피보나치 수를 저장할 곳을 만들고 따로 계산할 필요 없이 계산된 결괏값을 활용하면 중복 계산 없이 빠르게 계산할 수 있게 됩니다.
이렇게 계산한 값을 저장하고 필요할 때 다시 꺼내 쓰는 기법을 메모이제이션이라 합니다.
bottom-up 방법
int[] dp = new int[n + 1];
dp[1] = 1;
if (n < 2) // n이 2보다 작으면 f(0) = 0, f(1) = 1
return n;
else {
// f(n) = f(n - 1) + f(n - 2)
// 배열에 결괏값을 집어넣는다
for (int i = 2; i <= n; i++)
dp[i] = dp[i - 1] + dp[i - 2];
return dp[n];
}top-down 방법
혹은 아래와 같이 풀 수도 있습니다.
(로직만 간단하게 보여드리기 위해 작성한 코드로 실제 동작하는 코드와는 차이가 있습니다.)
public static int[] result = new int[n + 1];
public int fibonacci(int[] dp, int n) {
// 이미 저장된 값이면 해당 값을 리턴
if (dp[n] != 0)
return dp[n];
// 초깃값
if (n < 2)
return n;
// 계산된 값을 저장하고 리턴
return dp[n] = fibonacci(n - 1) + fibonacci(n - 2);
}이처럼 이전 결괏값을 어떻게 활용할 수 있을지 발견하는 것이 다이나믹 프로그래밍의 핵심!
🤦♀️ 하지만 이렇게 쉽기만 하다면 얼마나 좋겠어요
아마 이 글을 검색해서 들어오신 많은 분들은 위 예시보다는 훨씬 난도가 높은 문제를 맞닥뜨리고 오셨을 것입니다.
하지만 다이나믹 프로그래밍은 알고리즘이 아닌 하나의 패러다임으로, 문제를 어떻게 잘게 분해하고 연관성을 찾는지는 풀이하는 사람의 몫입니다.

이 글을 읽고 계신 분들의 표정 상상도...jpg
안타깝지만 다이나믹 프로그래밍에 왕도는 없습니다. 많은 문제를 풀어 보시면서 점화식을 세우는 연습이 답입니다.
저도 다이나믹 프로그래밍에 무지하게 약한 만큼 머리를 싸매다가 풀이를 본 적이 많았습니다.
그리고 단순명료한 점화식과 풀이를 보고는 이불을 걷어찹니다
연습, 그리고 연습
작정하고 어렵게 만들면 사경을 헤매게(?) 만들 수도 있고,
방향을 잘못 잡으면 정말 밑도 끝도 없이 사고의 나락으로 빠져드는 게 다이나믹 프로그래밍입니다.
그렇기에 시간을 정해 두고 도저히 풀리지 않는다면 풀이를 참고하면서 자기 것으로 만드는 것도 좋습니다.
언제나 그렇듯 Problem solving은 연습... 연습만이 살 길입니다.
여담, 그냥 헛소리
이름은 참 거창한 "다이나믹" 프로그래밍인데, 사실 딱히 다이나믹하지는 않습니다.
그렇기에 전공자의 시각에서 보면 대체 이 알고리즘의 어디가 다이나믹하다는 거야? 라고 생각하기 쉽습니다.
그런데 다이나믹 프로그래밍이라는 기법을 만든 리처드 벨만도 단순히
dynamic이라는 단어 너무 멋지지 않냐?!
같은 생각으로 명명했다는 우스갯소리가 있는데, 믿거나 말거나.
