주의: 본 포스트는 저자가 학습하면서 작성한 글이므로 잘못된 내용이 있을 수 있습니다.
지적과 제언은 언제든지 환영입니다.
✏️ 들어서며
중간 삽입, 삭제가 안 되는 선형 리스트
앞서 알아본 연결 리스트는 원소의 삽입, 삭제가 비교적 자유롭습니다. 찾는 위치까지 이동한 다음 작업을 수행해야 하지만 적어도 작업을 수행할 수는 있습니다.
이번에 알아볼 자료 구조인 선형 리스트는 연결 리스트와 다르게 삽입과 수정은 한쪽 또는 양쪽 끝에서만 가능합니다.
근데 이런 게 필요해?
그런데 이런 자료 구조가 왜 필요할까요? 중간 원소도 못 뽑고 앞뒤로만 접근해야 하는 자료 구조가 의미가 있을까요?
연결 리스트는 삽입과 삭제가 간편하지만 연산마다 링크를 재설정해야 하는 등 구현과 실제 연산이 복잡합니다. 반면 스택과 큐(덱도 포함합니다)은 맨 끝만 접근하면 되므로 구현이 매우 간단하고 빠릅니다.
그렇기에 선입선출(First-in-first-out, FIFO)이나 후입선출(Last-in-first-out, LIFO)이 필요한 상황에서 굳이 연결 리스트를 쓸 필요가 없습니다.
상황에 따라서 스택과 큐가 유리한 상황이 분명히 있으므로 우리는 이 상황을 파악하여 적절한 자료 구조를 선택, 사용하면 됩니다.
각 자료 구조에 대한 구현은 연결 리스트의 구현에서 일부 메서드를 제거하면 가능하므로 생략하였습니다.
스택 📚
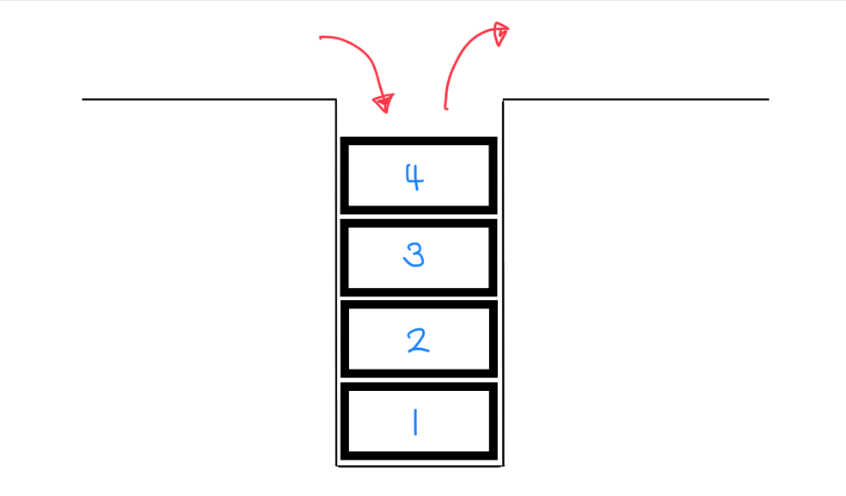
스택은 마지막에 들어간 데이터가 처음에 나오는 후입선출 자료 구조입니다.
안에 책이 쌓여 있는 박스를 열었을 때 마지막으로 넣은 책부터 빼는 것을 스택으로 비유할 수 있습니다.
스택에는 아래 두 가지 연산이 있습니다.
- push
- pop
Push
스택에 요소를 삽입하는 연산입니다.
정해진 위치의 끝에만 삽입하므로 시간복잡도는 관계 없이 항상 O(1) 입니다.
Pop
스택에 들어 있던 요소를 꺼내는 연산입니다.
정해진 위치의 끝에서만 꺼내므로 탐색은 필요하지 않고, 따라서 시간복잡도는 항상 O(1) 입니다.
큐 🚶🚶🚶
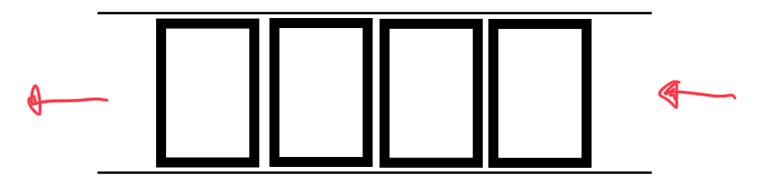
큐는 처음에 들어간 데이터가 처음에 나오는 선입선출 자료 구조입니다.
큐에는 아래 두 가지 기본 연산이 있습니다.
- enqueue
- dequeue
Enqueue
큐에 요소를 삽입하는 연산입니다. 스택과 마찬가지로 정해진 방향으로만 삽입하므로 시간 복잡도는 O(1) 입니다.
Dequeue
큐의 정해진 위치에서 요소를 제거하는 연산입니다. 정해진 방향에서만 (삽입 위치의 반대) 제거하므로 시간 복잡도는 O(1) 입니다.
덱 ↔️🚶🚶🚶↔️
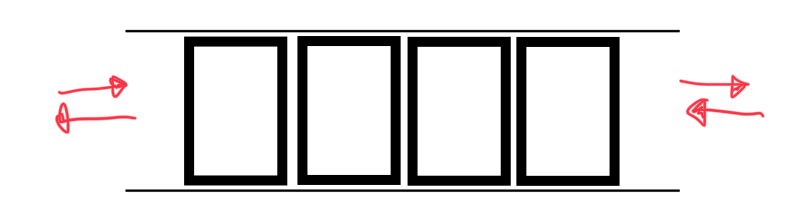
덱(Deque; Double-ended queue)는 데크라고도 부르며 양 끝에서 삽입, 삭제 연산을 할 수 있는 자료 구조입니다. 큐가 양방향으로 있다고 생각하면 쉽습니다.
덱에는 아래 네 가지 기본 연산이 있습니다.
- push_first
- push_last
- pop_first
- pop_last
Push
덱의 양 끝에 요소를 삽입하는 연산입니다. 두 정해진 지점으로만 삽입하므로 push_first, push_last 모두 시간 복잡도는 O(1) 입니다.
Pop
덱의 양 끝에서 요소를 제거하는 연산입니다. 두 개의 정해진 지점으로만 삭제가 이루어지므로 앞, 뒤 관계없이 시간 복잡도는 O(1) 입니다.
🧹 마치며
사실 앞서 구현한 연결 리스트 구조를 내부적으로 활용하는 일은 굉장히 드뭅니다. Java의 LinkedList는 넉넉한 크기의 배열을 생성하여 필요할 때마다 추가 확장하는 방법으로 구현되어 있으며 Python의 C 구현체인 CPython 또한 배열을 동적 할당하고 필요할 때마다 확장하고 있습니다.
연결 리스트로 비교적 쉽게 구현할 수 있지만, 시간이 된다면 연결 리스트가 아닌 배열로 스택과 큐를 직접 구현해보는 것도 좋습니다.
다음 포스트에서는 트리에 대해 다루겠습니다. 읽어 주셔서 감사합니다.
