🔗 링크
https://programmers.co.kr/learn/courses/30/lessons/62048
✏️ 문제
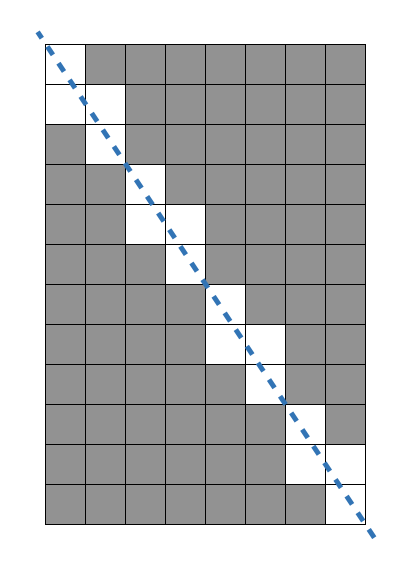
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.
🧠 접근
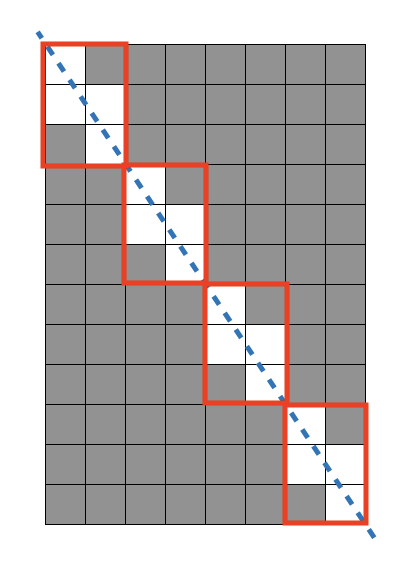
문제의 예시 그림에서 생각해야 할 것은 크게 두 가지입니다.
1) 빨간 사각형으로 표시된, 반복되는 사용 불가능 격자를 둘러싸는 조각의 개수.
2) 조각에서 사용할 수 없는 격자의 개수.
접근 1
예시의 그림을 상하 반전하고, 전체 직사각형의 왼쪽 아래 꼭짓점을 좌표평면의 원점이라고 가정하면 절취선은
y = ax (단, 0 ≤ a ≤ w)와 같은 일차함수 형태가 됩니다.
그림으로 나타내면 아래와 같습니다.
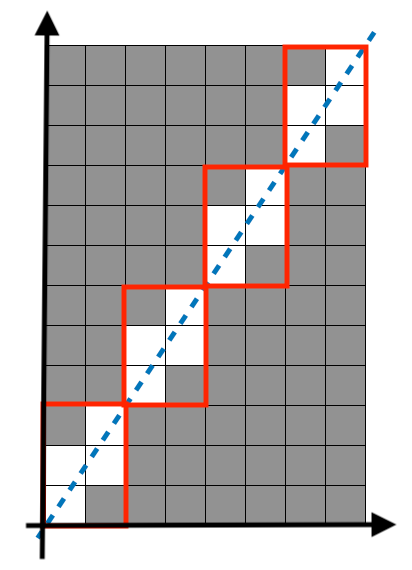
그러면 조각의 개수는 0 < x ≤ w 일 때 (w는 전체 사각형의 가로 길이) x 와 y = ax 가 모두 자연수인 점의 개수가 됩니다.
# 나누어 떨어지는 단위를 찾음
while y <= h:
x += 1
y = h * x / w
if y.is_integer(): # x 좌표와 y 좌표가 모두 정수이면 하나의 단위(조각)가 됨
break
pieces = int(h / y) # 나누어 떨어지는 조각 수 (예시 입력에서는 4개 조각)접근 2
접근 1에서의 그림과 같이 절취선을 일차함수라고 할 때 x 값을 점차 증가시키면 격자와 만나게 됩니다. 이 때 격자와 만나는 점을 기준으로 사용할 수 없는 다음 정사각형과 만납니다.
하나의 조각 안에서 만나는 점을 직사각형 위에 표시하면 아래와 같습니다.
.png)
즉, 점의 개수는 다음 사용할 수 없는 정사각형으로 넘어가는 횟수이므로 작은 사각형에서 사용할 수 없는 정사각형의 개수는 (조각 내에서 절취선과 격자의 교점의 개수 + 1) 과 같습니다.
절취선과 격자의 교점은 x 나 y 의 값이 하나 이상 자연수인 점이므로 조각의 폭과 높이에서 각각 1을 뺀 값이 해당 점의 개수가 됩니다.
unable_parts = int(x - 1) + int(y - 1) + 1예시에서 조각 내의 사용할 수 없는 정사각형의 개수는 (2 - 1) + (3 - 1) + 1 = 4가 됩니다.
마무리
접근 1에서 구한 '조각의 개수'와 접근 2에서 구한 '사용할 수 없는 정사각형'의 개수를 이용하면 사용할 수 있는 정사각형의 개수를 구할 수 있습니다.
answer = w * h - pieces * unable_parts그런데 문제가 있다?
이 방법은 대부분의 상황에서 빠르지만 전체 직사각형의 한 변이 지나치게 길 경우, 가령 w = 100000000, h = 1일 때에는 조각의 개수를 찾는 방식의 특성상 조각의 크기가 하나 뿐이므로 직사각형 전체를 스캔해 매우 긴 시간이 소요되게 됩니다.
그러나 조각이 하나일 때에는 대각선이 전체를 가로지르므로 사용할 수 있는 정사각형의 개수가 0임을 쉽게 알 수 있습니다.
따라서 아래와 같이 예외 처리를 하여 문제를 해결하였습니다.
# w = 100000000, h = 1인 경우와 같이
# 한 축이 너무 길 때 시간 초과 방지
if w == 1 or h == 1:
return 0문제에 대해 검색해 보니 조각의 개수가 직사각형의 높이와 폭의 최대공약수라는 설명이 많았고 이 방법을 사용하면 상기한 문제가 발생하지 않지만, 왜 그런지 이해하기 힘들어 조금 더 직관적인 해결 방법을 찾게 되었습니다.
📄 전체 소스 코드
import math
def solution(w,h):
x = 0
y = 0
# w = 100000000, h = 1인 경우와 같이
# 한 축이 너무 길 때 시간 초과 방지
if w == 1 or h == 1:
return 0
# 나누어 떨어지는 단위를 찾음
while y <= h:
x += 1
y = h * x / w
if y.is_integer(): # x 좌표와 y 좌표가 모두 정수이면 하나의 단위가 됨
break
pieces = int(h / y) # 나누어 떨어지는 조각 수 (예시 입력에서는 4개 조각)
'''
하나의 단위공간에서 쓸 수 없는 정사각형의 수는
직사각형의 시작과 끝, 다음 조각으로 이어지는 점을 제외하고
x = n 또는 y = n (n은 자연수) 을 만족하는 n의 개수 + 1과 같음
'''
unable_parts = int(x - 1) + int(y - 1) + 1
answer = w * h - pieces * unable_parts
return answer