[알고리즘] Monotonic Stack

SIK407·2025년 5월 21일

Monotonic 스택 monotonic stack 모노토닉 스택

알고리즘

목록 보기

4/7

참을 인 Stack Overflow...
...

어떻게 잘 살아남으셨겠죠...?

📃 예시 문제

[백준] 2493 - 탑

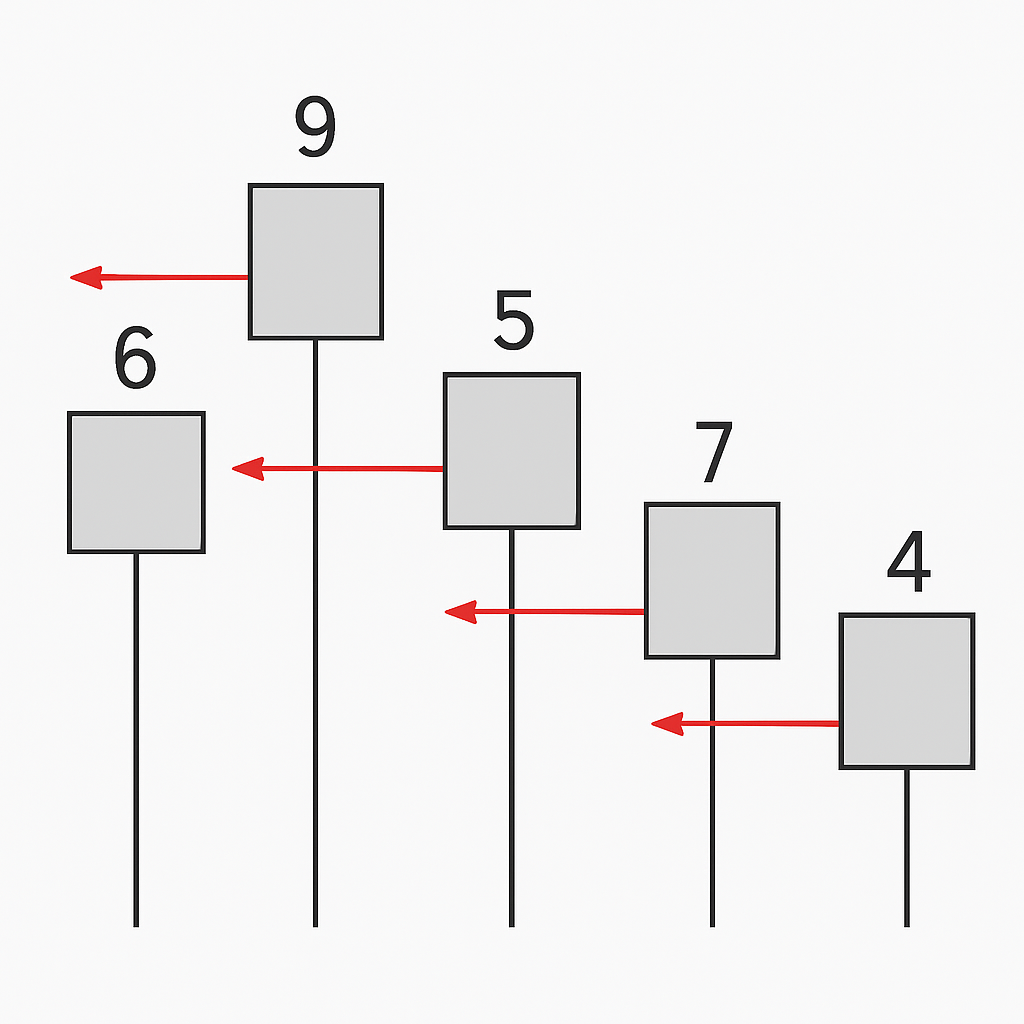
그림이 좀 이상하게 그려졌지만...
결론부터 말하면 이 문제는, 우측 탑부터 레이저를 쏘는데, 앞에 더 큰 탑이 있으면 그 레이저를 받는다.

즉,
"지금 index 다음으로 큰 값의 Index 찾기"다

📍설명

Monotonic Stack (단조 스택)
Stack의 element들이 오름, 내림 차순으로 유지하는 알고리즘 기법

※ Monotonic (단조): 함수의 증가 또는 감소 경향이 일정하게 유지되는 특성

이 스택은 크게 두 가지 유형이 있다.

유형	설명
증가 스택 (Increasing)	Stack이 오름차순을 유지, 새로운 값이 peek() 보다 클 때까지 pop()
감소 스택 (Decreasing)	Stack이 내림차순을 유지, 새로운 값이 peek() 보다 작을 때까지 pop()

지금부턴, 위 문제 예시와 증가 스택을 예시로 설명하겠다.

int[] arr = { 6, 9, 5, 7, 4 };

이러한 배열이 있다.

1. arr[0] = 6

Stack Peek: 빈 상태
Stack이 비어 있으므로 [0] 값을 스택에 push()

STACK
6

2. arr[1] = 9

Stack Peek: 6
[1]의 값보다 큰 값이 나올 때까지, pop()을 한다.
그러면.... Stack에 있는 모든 값이 다 사라진다..

그 다음, [1]의 값을 push() 한다.

STACK
9

3. arr[2] = 5

Stack Peek: 9
[2]의 값보다 큰 값이 나올 때까지, pop()을 한다.
엇? 지금 Peek()의 값이 [2]보다 크다.

그러면... [2]에서 가장 가까운 값 중, [2]보다 큰 값은 9가 된다.

그리고 마찬가지로 [2]의 값도 push()를 해준다.

STACK
5 9

4. arr[3] = 7

Stack Peek: 5
[3]의 값보다 큰 값이 나올 때까지, pop()을 한다.
그럼 현재 5는 사라지게 되고, 9가 남는다.

STACK
9

그러면... [3]에서 가장 가까운 값 중, [3]보다 큰 값은 9가 된다.

그리고 마찬가지로 [3]의 값도 push()를 해준다.

STACK
7 9

4. arr[4] = 4

Stack Peek: 7
[4]의 값보다 큰 값이 나올 때까지, pop()을 한다.
peek()가 [4]보다 크다.

그러면... [4]에서 가장 가까운 값 중, [4]보다 큰 값은 7가 된다.

그리고 마찬가지로 [4]의 값도 push()를 해준다.

STACK
4 7 9

이런식으로 진행하면 된다.

public static void solution(int N, int[] arr) {
    Stack<int[]> s = new Stack<>();

    for (int i = 0; i < N; i++) {
        int h = arr[i];

        while (!s.isEmpty()){
            if (h < s.peek()[1]) {
                System.out.print(s.peek()[0] + " ");
                break;
            }
            s.pop();
        }

        if (s.isEmpty()) System.out.print(0 + " ");

        s.push(new int[]{i + 1, h});
    }
}