무시무시한 부산의 고소공포증 다리...
엄청 길고 엄청 높아서 운전자들을 공포에 떨게 하는 곳.... 😱
이 사진을 왜 올렸나면,
이번에 배울 알고리즘 이름이 최장 부분 수열 이라는 알고리즘이다.
맞다.
그냥 길고 높아 보여서 가져온 다리 사진이다.
📃 예시 문제
[백준 S2] 11053 - 가장 긴 증가하는 부분 수열
[백준 G4] 2631 - 줄세우기
📍설명
| 3 | 7 | 5 | 2 | 6 | 1 | 4 |
|---|
이러한 수열이 있다고 가정하자.
부분 수열은 당연히 여러가지가 나온다.
| 3 | 5 | 6 | 1 |
|---|
요런 것도 있고,
| 3 | 7 |
|---|
요럴 수도 있고,
| 3 | 5 | 6 | 1 | 4 |
|---|
요렇게도 되고
이런 부분 수열 중, 계속 증가하는 부분 수열을 "증가 부분 수열"
가장 긴 부분 수열을 "최장 증가 부분 수열" 이라고 한다.
최장 증가 부분 수열(LIS, Longest Increasing Subsequence)
배열의 일부 원소를 골라내서 만든 부분 수열 중,
각 원소가 이전 원소보다 크다는 조건을 만족하고, 그 길이가 최대인 부분 수열
여러가지 해결 방안이 있지만, DP로 해결을 해보겠다.
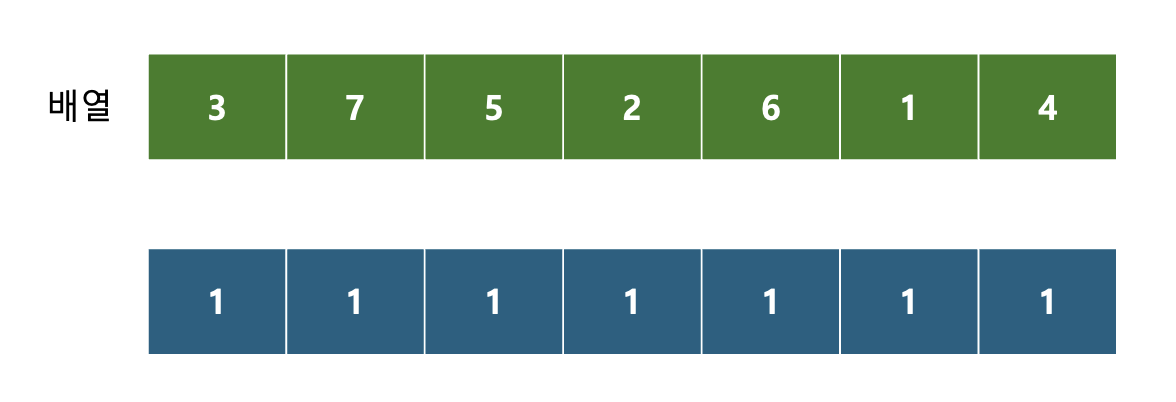
일단, 자기 자신을 포함하면 무조건 1개는 기본이다.
3을 기준으로 생각하자.
기준까지 나올 수 있는 부분 수열은 단 한개다.

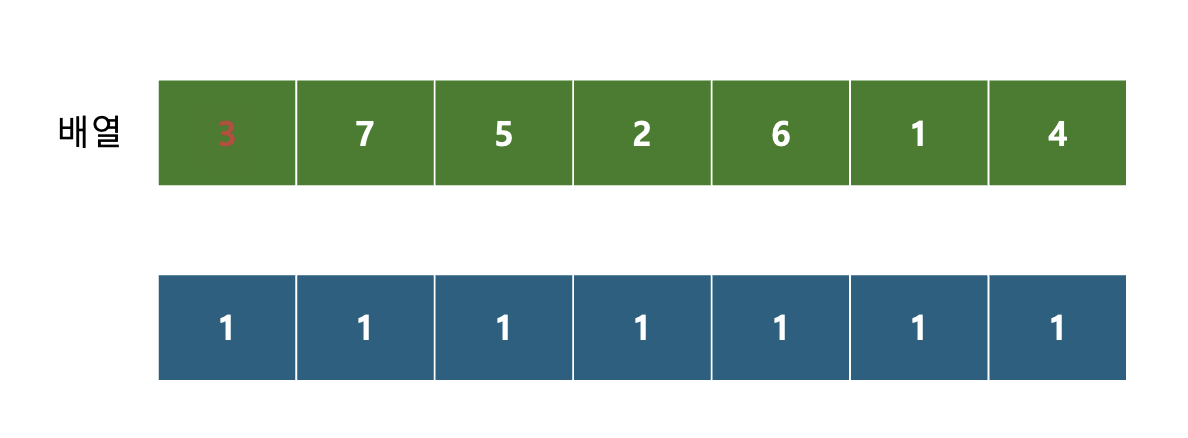
다음은 7이 기준이다.
7보다 앞에 있는 값들을 전부 하나씩 비교한다.
만약 기준보다 작은 값이면, 기준을 포함하면 새로운 증가 부분 수열이 나오게 된다.
3은 7보다 작다.
그래서 3의 dp 값에 1을 더한 값과, 7의 dp값을 비교해 최대값을 집어넣는다.
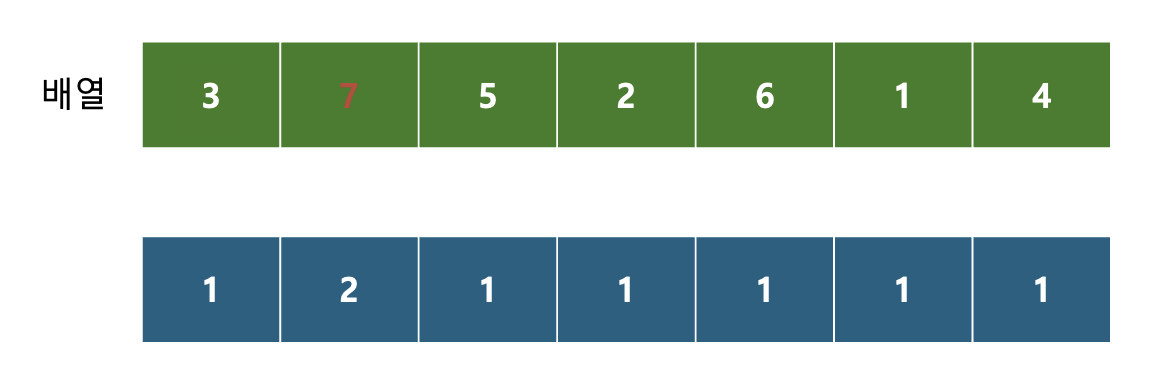
다음은 5가 기준이다.
앞에 3은 5보다 작기 때문에, 앞서 말했던 것처럼
그래서 3의 dp 값에 1을 더한 값과, 5의 dp값을 비교해 최대값을 집어넣는다.
7은 기준보다 크기 때문에, 5보다 앞에 올 수 없다.
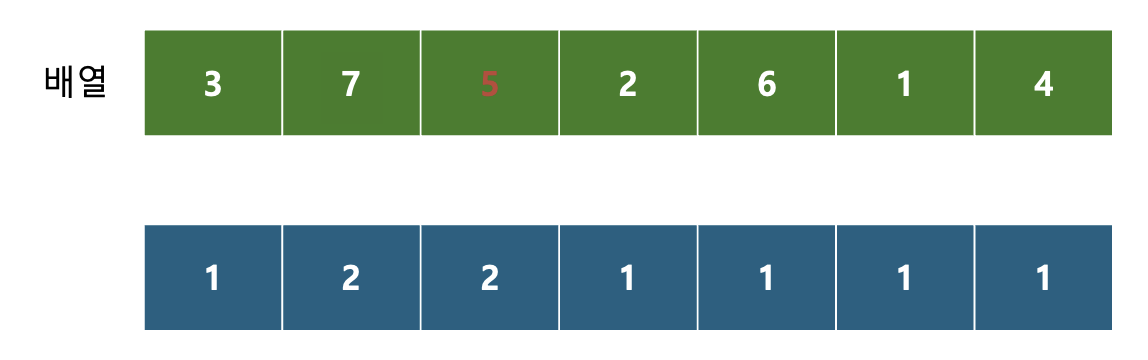
다음은 2가 기준이다.
기준보다 앞에 있는 값들이 전부 기준보다 크다...
PASS~~
다음은 6이 기준이다.
기준보다 앞에 있는 값 중, {3, 5}가 기준보다 작다.
3의 DP 값에 +1 한 값과, 기준의 DP 값을 비교한다.
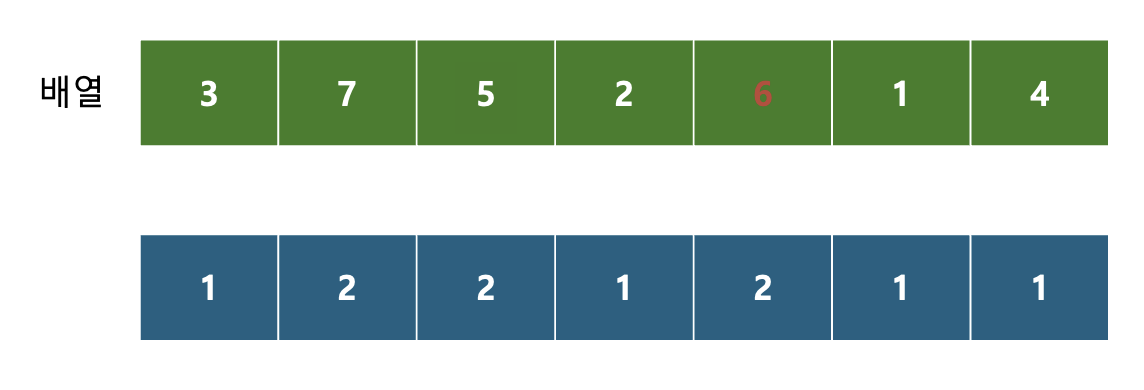
5의 DP값에 +1 한 값과, 기준의 DP 값을 비교한다.
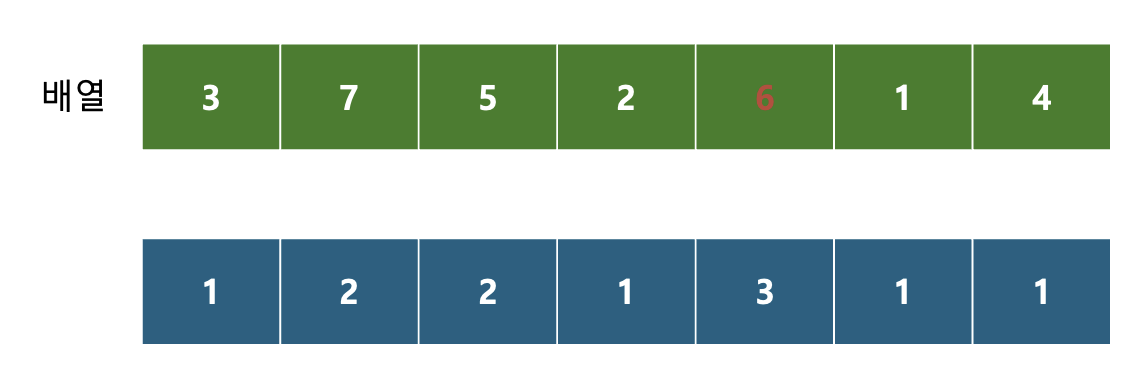
그리고 큰 값들을 넣어주면 된다.
이처럼 같은 과정을 반복하게 되면...
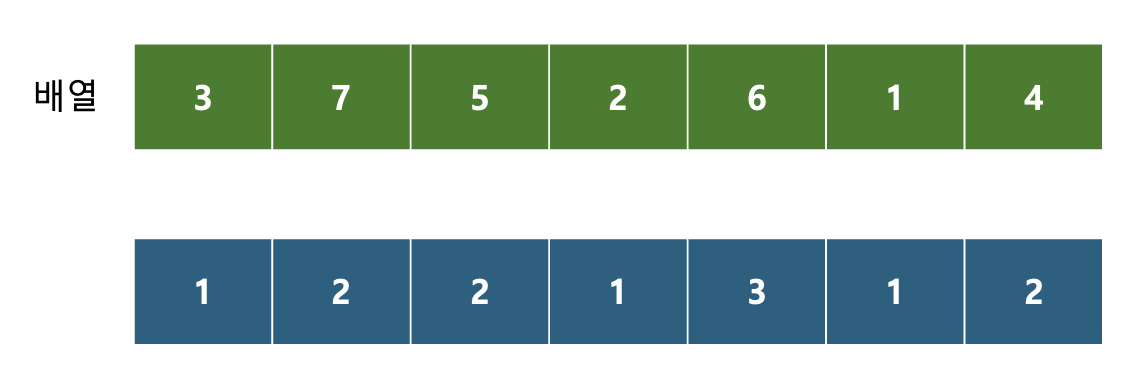
이렇게 된다.
LIS는 DP 배열 중, 가장 큰 값인 3이 된다.
점화식은
for (int i = 1; i < N; i++) {
for (int j = 0; j < i; j++) {
if (arr[i] > arr[j])
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}🗂️ 최종 개념 정리
(이진 탐색을 활용한 O(NLogN) 방식은 다른 글에서...)
이번 DP를 활용한 방식은 O(N²)이다.
기준보다 앞에 있는 배열에서,
나보다 작은 값의 부분 수열의 값을 가져와 MAX(최장) 연산을 진행한다.
dp[i] = max(dp[j] + 1)
단, 0 ≤ j < i 이고 arr[j] < arr[i]메모이제이션을 활용한 전형적인 DP 방식으로 진행했다.

