1. 알고리즘 1주차
1) 알고리즘이란?
어떤 문제의 해결을 위하여, 입력된 자료를 토대로 하여 원하는 출력을 유도해내는 규칙의 집합이다.
문제를 해결하기 위한 여러가지 방법들 중 가장 좋은방법을 고를 수 있다.
2) 알고리즘 연습하기
한가지 문제에 대해 여러 방법으로 문제를 해결해보면서 더 좋은 방법이 무엇일지 생각해본다.
3) 시간 복잡도란?
입력값과 문제를 해결하는데 걸리는 시간과의 상관관계
입력값이 2배로 늘어났을 때 문제를 해결하는 데 걸리는 시간은 몇 배로 늘어나는지!
-> 우리에게는 입력값이 늘어나도 걸리는 시간이 덜 늘어나는 알고리즘이 좋은 알고리즘이다!
- 시간 복잡도 연산 방법
각 줄이 실행되는 것을 1번의 연산이 된다고 생각하면 된다.
입력값의 길이는 보통 N으로 표현한다.
여기서 입력값이란, 함수에서 크기가 변경될 수 있는 값!
예시 1)
=> N * N * 1 = N^2
예시 2)
=> 1 + N * 2 = 2N + 1
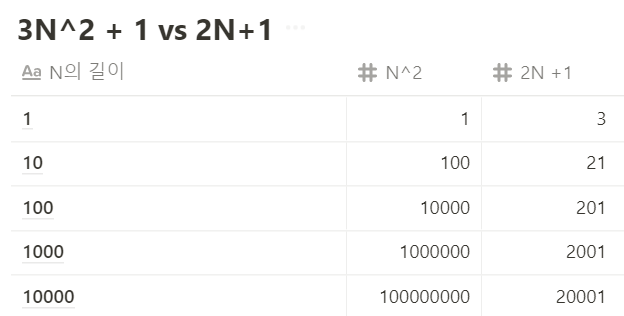
예시 1, 2를 비교하면?
=> 2N + 1이 숫자가 커질수록 효율적!
하지만, 보통 이렇게 자세하게 비교하지 않고 대략적으로만 확인한다.
상수는 신경쓰지 않고 입력값에 비례해서 어느정도로 증가하는지만 파악!
예를들면 예시 1번은 N^2, 예시 2번은 N으로 생각!!
4) 공간 복잡도란?
입력값과 문제를 해결하는 데 걸리는 공간과의 상관관계
입력값이 2배로 늘어났을 때 문제를 해결하는데 거리는 공간이 몇배로 늘어나는지!
-> 입력값이 늘어나도 걸리는 공간이 덜 늘어나는 알고리즘이 좋을 알고리즘이다!
- 공간 복잡도 연산 방법
저장하는 데이터의 양이 1개의 공간을 사용한다고 생각한다.
예시 1)
=> 26 + 1 + 1 + 1 = 29
번외❔) 이 코드의 시간복잡도는?
=> 26 * (1 + N * 2 + 3) = 52N + 104
예시 2)
=> 26 + 1 + 1 + 1 + 1 = 30
번외❔) 이 코드의 시간복잡도는?
N * (1 + 2) + 2 + 26 * (1 + 3) = 3N + 106
예시 1, 2를 비교하면?
=> 52N + 104 든 3N + 106 이든 N^2에 비해서는 큰 차이가 아니다
즉, 공간복잡도보다는 시간복잡도를 더 신경쓰자!!!
5) 점근 표기법이란?
알고리즘의 성능을 수학적으로 표기하는 방법, 알고리즘의 "효율성"을 평가!
어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 수론과 해석학의 방법이다.
-
빅오(Big-O)표기법
최악의 성능이 나올 때 어느 정도의 연산량이 걸릴것인지 표기 -
빅 오메가(Big-Ω)표기법
최선의 성능이 나올 때 어느 정도의 연산량이 걸릴것인지 표기
예를 들어 빅오 표기법으로 표기하면 O(N), 빅 오메가 표기법으로 표기하면 Ω(1)의 시간복잡도를 가진 알고리즘이다.
예시)

=> N * 1 = N
빅오 표기법 = O(N)
빅 오메가 표기법 = Ω(1)
이처럼 알고리즘의 성능은 항상 동일하지 않고 입력값에 다라서 달라질 수 있다.
하지만 알고리즘에서는 보통 거의 모든 알고리즘을 빅오 표기법을 분석한다.
대부분의 입력값이 최선일 경우는 거의 없고, 최악의 경우를 대비해야 하기 때문!
💜 오늘 느끼고 배운 점
오전 오후 : 알고리즘 인터넷 강의 수강
저녁 : 거북이반 복습강의 수강
평소에 백준 알고리즘 문제를 풀며 알고리즘이 무엇일까 궁금했는데 이를 해결할 수 있는 강의였다.
알고리즘 강의를 통해 어떻게 코드를 작성해야 좋은코드를 작성할 수 있을 지 알게되었다. 앞으로 시간복잡도를 생각하며 코드를 작성 해 봐야겠다.