[Baekjoon][Python] 2776번 암기왕

2776번 암기왕

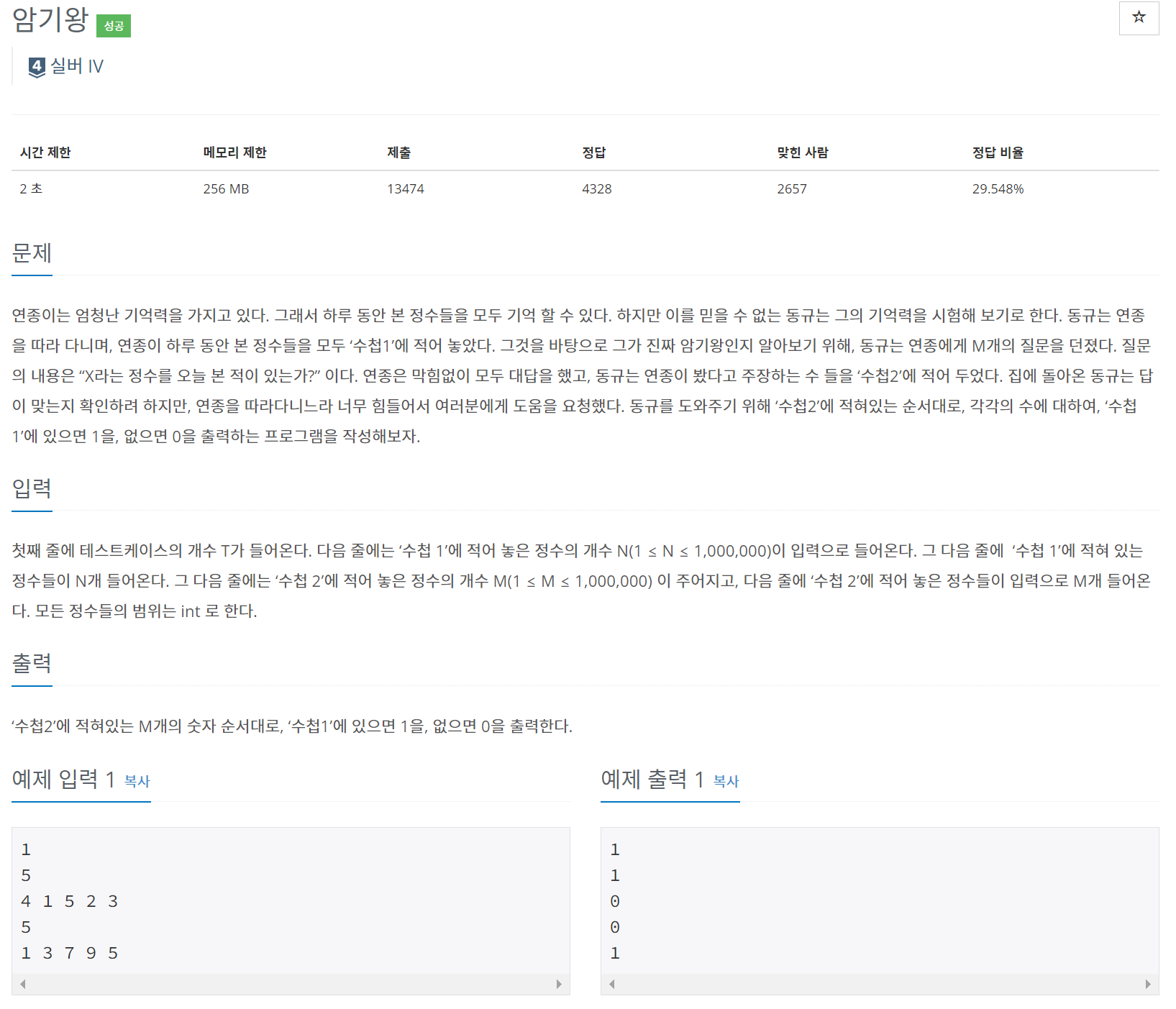
문제

풀이

파이썬으로 가능한 여러 가지 풀이 중 2가지를 소개하겠다

1. Binary Search
   이진 탐색을 사용하여 조회하면 된다.
   검색이 O(logN) 이지만, 단점으로는 배열이 정렬되어 있어야 한다는 것이 있다.
   정렬 되어 있지 않은 배열이기 때문에 코드에서 정렬을 해주었다.

   import sys
   
   def binarySearch(arr, x):
       start = 0
       end = len(arr) - 1
       while True:
           if start > end:
               return -1
           index = (start + end) // 2
           if arr[index] < x:
               start = index + 1
           elif arr[index] > x:
               end = index - 1
           else:
               return index           
   
   # 테스트 케이스 개수
   T = int(sys.stdin.readline())
   
   for i in range(T):
       # 수첩1 정수 개수
       N = int(sys.stdin.readline())
       original = list(map(int, sys.stdin.readline().split()))
       original.sort()
       # 수첩2 정수 개수
       M = int(sys.stdin.readline())
       new = list(map(int, sys.stdin.readline().split()))
   
       for num in new:
           if binarySearch(original, num) >= 0:
               print(1)
           else:
               print(0)

   

2. 파이썬 in 문법
   파이썬 내장 문법 중 in을 사용해 간단하게 해결할 수도 있다. in연산자는 멤버십 연산자로 문자열이나 리스트나 튜플과 같이 연속적인 자료구조에 속한 멤버를 확인하기 위한 연산자이다.
   하지만 신기한 것이 binary search보다 시간도 훨씬 적게 들어 조금 깊게 찾아보게 되었다.

   시간 복잡도 (참고)

   • list, tuple
     Average: O(n)
     하나하나 순회하기 때문에 데이터의 크기만큼 시간 복잡도를 갖게 됩니다.
   • set, dictionary
     Average: O(1), Worst: O(n)
     내부적으로 hash를 통해서 자료들을 저장하기 때문에 시간복잡도가 O(1)가 가능하고 O(n)의 경우에는 해시가 성능이 떨어졌을(충돌이 많은 경우) 때 발생합니다.

   위에서 보듯이 list의 set의 경우 평균 O(1)의 시간복잡도를 가지고, 정렬 또한 거치지 않았으므로, 실행 시간의 차이가 크게 난 것 같다.

   for _ in range(int(input())):
       # 수첩1 정수 개수
       input()
       original = set(input().split())
   
       # 수첩2 정수 개수
       input()
       new = input().split()
   
       for num in new:
           if num in original:
               print(1)
           else:
               print(0)

   
   

결론

이렇게 다양한 풀이가 존재하는데, 나 역시 다양하게 경험해보는 것이 좋은 것 같다. 이번 기회에 파이썬의 in 연산자에 대해서도 조금 더 자세히 알게 되어 좋게 생각한다.