1. 오늘 주제

유니티로 게임개발을 하면서 자주 사용하게 될 삼각함수에 대해서 알아 보려고 한다.
삼각함수는 삼각형의 각도와 변의 길이 사이의 관계를 설명하는 함수로, 주로 직각삼각형에서 각과 변의 비율을 기반으로 정의 된다.

주요 삼각함수

• 사인(Sine, $sin$)
  정의 : 직각삼각형에서 특정 각도의 반대변의 길이를 빗변의 길이로 나눈 값.
  식 : ${sin(\theta)}={높이=O\over빗변=H}$
  

• 코사인 (Cosine, $cos$)
  정의 : 직각삼각형에서 특정 각도의 인접변의 길이를 빗변의 길이로 나눈 값.
  식 : ${cos(\theta)}={밑변=A\over빗변=H}$

• 탄젠트 (Tangent, $tan$, 접한것 or 기울기)
  정의 : 직각삼각형에서 특정 각도의 인접변의 길이를 빗변의 길이로 나눈 값.
  식 : ${tan(\theta)}={높이=O\over밑변=A}$

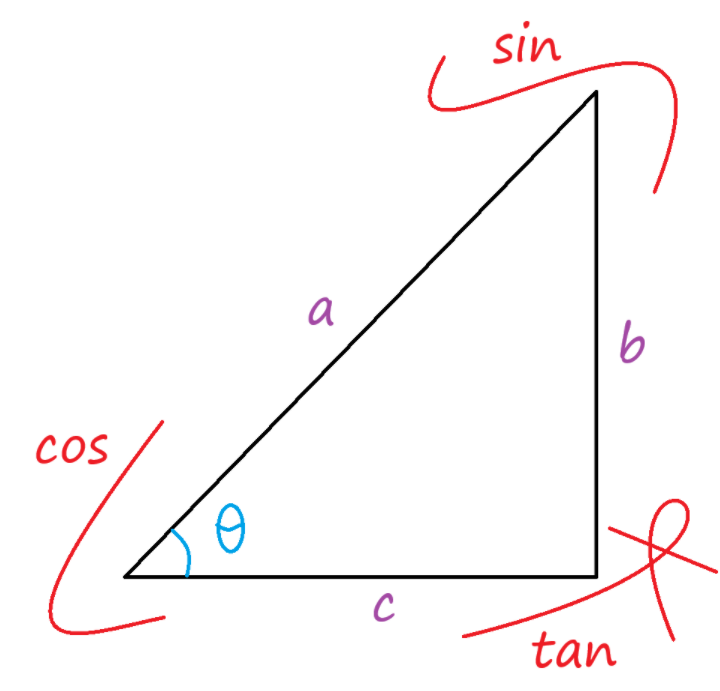일반적인 삼각함수에 대한 이미지

위 그림 처럼 외우면 되겠지 생각했지만, 외우는 것에는 자신이 없기 때문에 이해하는게 먼저라고 생각하기 때문에 어느정도 정리를 해보았다.

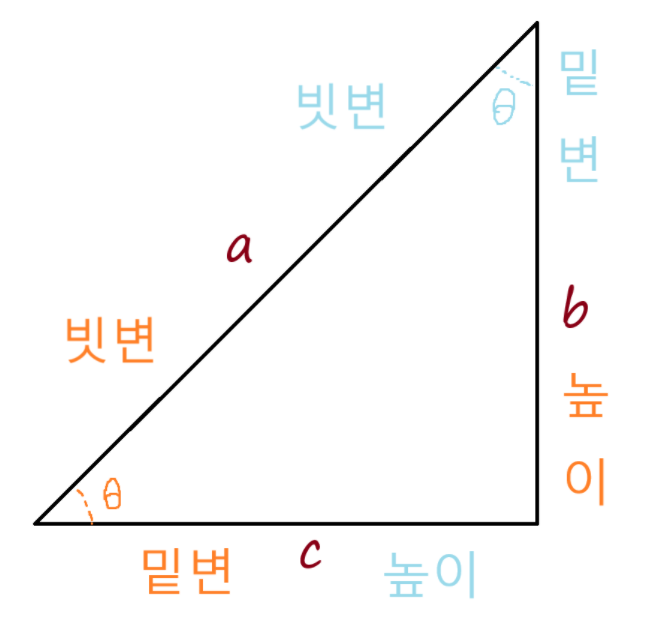생각하면서 외워보자..

$sin(\theta)$ 와 $cos(\theta)$ 는 결국 $\theta$가 어디에 있냐에 따라 ${c\;or\;b\over a}$기 떄문에 빗변이 분모로 높이와 밑변이 분자로 알아두면 되고, $tan$ 경우에는 $tan(\theta)={sin(\theta)\over cos(\theta)}$ 밑변을 가진 $cos(\theta)$가 분모고 높이를 가진 $sin(\theta)$가 분자로 생각하면 외우는데는 어렵지 않을 것 같다.

그리고
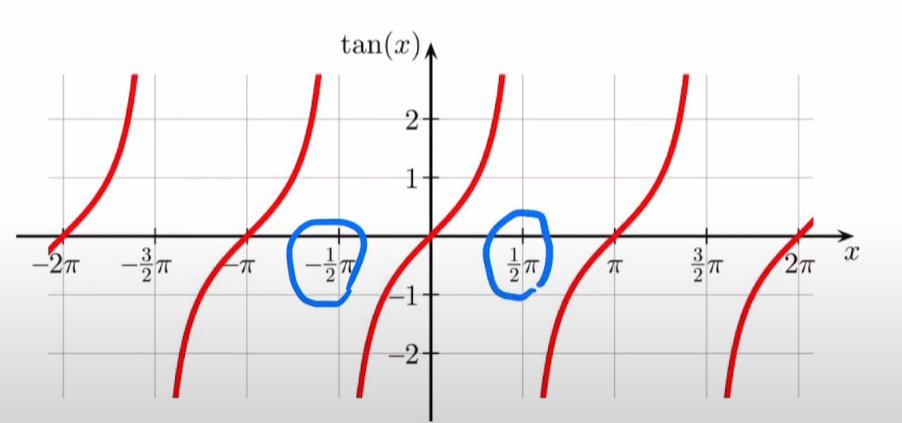
$tan$의 경우는 아래 그림처럼 각도가 $-{1 \over 2}\pi$ 부터 ${1 \over 2}\pi$까지 계속 반복이 된다. 이유는 직각삼각형에서 반대변을 인접변으로 나눈 값이라, 인접변이 0이 되는 순간에는 나누기가 불가능하기 때문이다. 수학적으로 이 각도에서 탄젠트 함수는 무한대($-\infin$ ~ +$\infin$)로 발산하기 때문에 값이 없다.

• 아크탄젠트 (Arc Tangent, $atan$)
  정의 : 탄젠트의 역함수 기호로는 $atan$ 또는 $tan^{-1}$, 주어진 탄젠트 값을 사용하여 그에 해당하는 각도를 반환
  (탄젠트 함수가 각도로부터 비율을 구하는 함수라면, 아크탄젠트는 비율로부터 각도를 구하는 함수)
  식 : ${\theta}=tan^{-1}({높이=O\over밑변=A})$
  

$atan$의 경우 게임 개발에서 많이 사용한다.
그러나 수학 공식 그대로 사용했을 때는 $tan$과 비슷한 이유로 문제가 발생한다.
$atan$ 함수는 각도의 범위가 $-{\pi \over 2}\leq{\theta}\leq{\pi \over 2}$ 즉, -90도에서 90도까지의 값만 반환되기 때문에, 결과적으로 올바른 사분면을 구분하지 못할 수 있다.

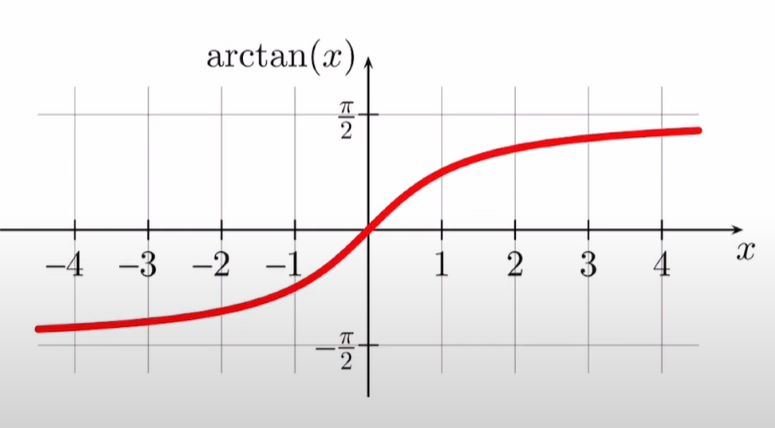
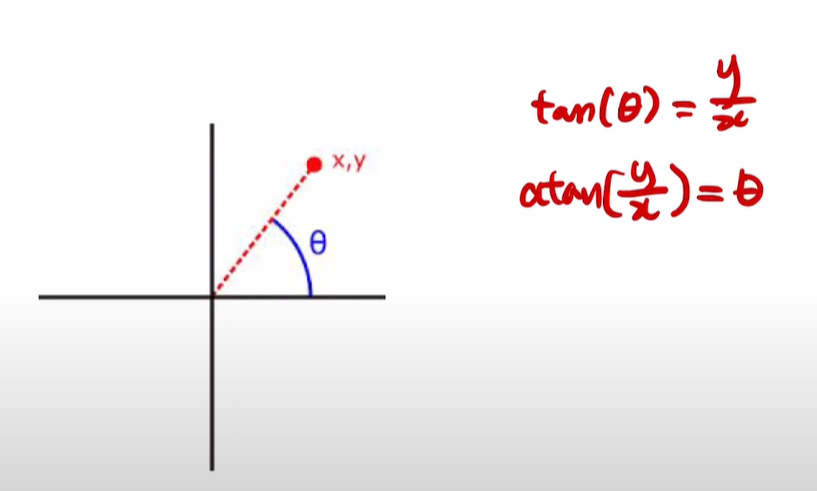
예를 들어, $y \over x$의 값이 양수일 때, 1사분면에 있는지 3사분면에 있는지 구분 할 수 있어야 하는데, 아래 그림처럼 대칭되는 사분면을 가지고 치환하려고 하면 원래 있던 매핑정보가 사라지기 때문에 게임 개발 시에는 $atan({y \over x})$가지고는 어느쪽 각도인지를 알 수 가 없다.

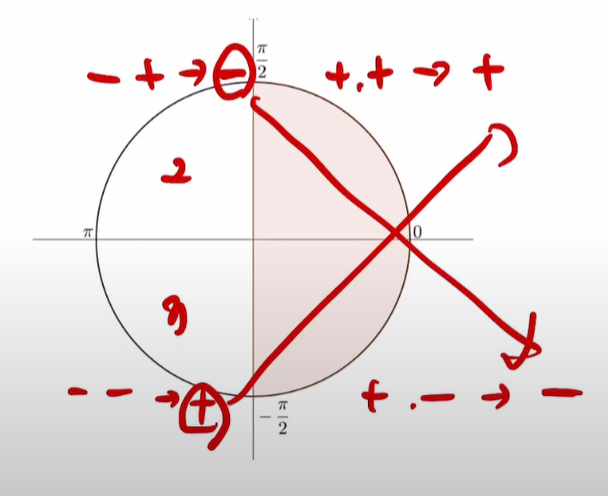
그래서 $atan2(y,x)$를 많이 사용하게 되는데 이렇게 하면 y와 x를 가지고 몇사분면인지를 알아내고, $atan$ 값까지 구할 수 있게 된다.

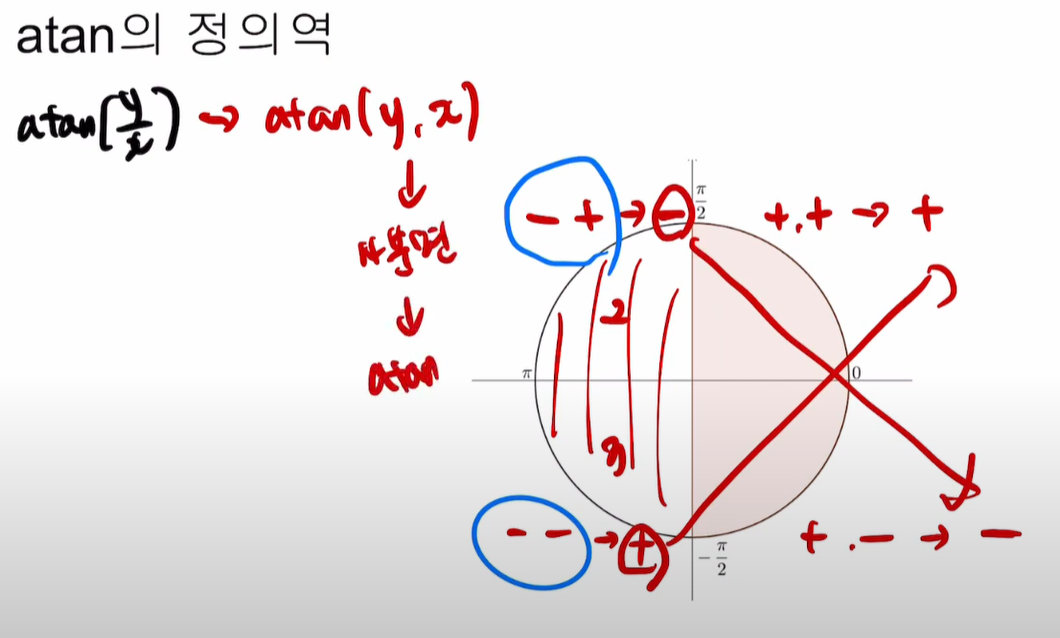
y와 x 값을 직접 받아서 사분면까지 고려한 각도를 반환하므로, 보다 정확한 계산이 가능하다.

2. 어디다 사용하나..

삼각함수를 어느정도 통달한다면 게임 개발에서 많은 일을 할 수 있다.
예를 들면... ChatGPT가 알려주길..

1. 캐릭터 회전 및 방향 설정
   삼각함수를 사용하여 캐릭터가 특정 각도로 회전하거나 특정 방향을 바라보도록 할 수 있습니다. 특히 atan2() 함수는 캐릭터가 목표 좌표로 회전할 때 많이 사용됩니다.
   예: 2D 게임에서 플레이어가 마우스를 향해 바라보는 기능.
2. 투사체 궤적 계산
   총알, 화살, 레이저 등의 투사체가 목표 방향으로 날아가도록 구현할 때 삼각함수를 활용하여 투사체의 궤적을 계산할 수 있습니다.
   예: 포물선 운동을 구현할 때, 사인과 코사인으로 각도에 따른 위치 변화 계산.
3. 진자 운동 및 회전 운동
   진자처럼 일정한 주기를 가진 운동이나 회전 운동을 구현할 때 삼각함수가 유용합니다. 이를 통해 부드러운 스윙 효과나 반복적인 애니메이션을 구현할 수 있습니다.
   예: 그네 운동, 진자 시뮬레이션, 시계 추의 흔들림.
4. 캐릭터 이동 패턴
   삼각함수를 활용하여 캐릭터가 원형 궤도를 따라 움직이거나, 파도 모양의 이동 경로를 따르는 등의 다양한 이동 패턴을 만들 수 있습니다.
   예: 적이 원형으로 빙빙 도는 패턴, 물고기나 비행기의 파동형 이동.
5. 카메라 흔들림 및 회전
   게임 내에서 카메라가 부드럽게 흔들리거나 회전할 때, 삼각함수를 사용하여 자연스러운 움직임을 만들 수 있습니다.
   예: 폭발 후 카메라가 흔들리는 효과.
6. 원형 UI 요소 배치
   삼각함수를 사용하여 UI 요소나 버튼을 원형으로 배치할 수 있습니다. 특정 각도에 맞춰 배치할 때 각 요소의 위치를 계산할 수 있습니다.
   예: 방사형 메뉴나 원형 미니맵 구현.
7. 광원 계산 및 그림자 처리
   삼각함수를 사용하여 광원의 방향과 각도에 따른 그림자 처리나 조명을 구현할 수 있습니다. 이는 게임의 현실감을 높여주는 중요한 요소입니다.
   예: 2D 게임에서 그림자가 물체의 각도에 따라 변하는 효과.
8. 카메라 궤적 이동
   카메라가 특정 궤적을 따라 이동하도록 구현할 때 삼각함수를 사용하여 자연스러운 곡선 경로를 따라 움직이게 할 수 있습니다.
   예: 특정 이벤트에서 카메라가 회전하거나 곡선을 따라 이동하는 연출.
9. 타이머나 주기적인 이벤트 발생
   sin() 또는 cos() 함수를 이용해 주기적인 이벤트나 효과를 만들 수 있습니다. 시간에 따라 변화하는 값으로 캐릭터나 환경의 특정 속성을 변경할 수 있습니다.
   예: 시간에 따라 밝기가 변하는 빛, 주기적인 적 공격 패턴.
10. 카메라 줌 효과
    삼각함수를 사용하여 카메라가 부드럽게 줌 인/아웃을 하도록 만들 수 있습니다. 이를 통해 화면 전환 시 자연스러운 확대/축소 효과를 구현할 수 있습니다.
    예: 보스 전투 중 카메라가 줌 인하여 긴장감을 높이는 연출.
11. 3D 모델의 뼈대 애니메이션
    3D 모델의 뼈대(본)가 특정 각도로 회전하거나 움직일 때, 삼각함수를 사용하여 각도를 계산하고 자연스러운 동작을 구현할 수 있습니다.
    예: 팔꿈치, 무릎 등의 관절 각도를 계산하여 캐릭터가 움직이는 방식.
12. 카메라의 구면 좌표 이동 (Polar Coordinates)
    구면 좌표계를 사용하여 카메라가 중심을 기준으로 회전하면서 일정한 거리를 유지하는 방식으로 구현할 수 있습니다.
    예: 3D 게임에서 플레이어를 중심으로 카메라가 궤도를 따라 회전하는 방식.

같은 다양한 일을 할 수 있게 된다.
언젠가는 응용해서 나도 해볼 수 있겠지..

3. 참조

https://www.youtube.com/watch?v=nGmJYCzk8gE&t=305s
https://www.youtube.com/watch?v=ikGOSX6TXy0