[WEEK03] DFS

DFS

DFS

DFS는 깊이 우선 탐색(Depth-First Search)로 루트 노드에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법이다. 예를들어 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 바업ㅂ과 유사하다. 즉, 넓게 탐색하기 전에 깊게 탐색하는 것이다. DFS를 사용하는 경우는 모든 노드를 방문하고자 하는 경우에 주로 사용된다. 깊이 우선 탐색이 너비 우선 탐색보다 좀 더 간단하다. 단순 검색 속도 자체는 너비 우선 탐색에 비해서 느리다.

DFS의 특징

• 자기 자신을 호출하는 순환 알고리즘의 형태를 가지고 있다.
• 전위 순회를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다.
• 이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다.
  - 이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.
  

DFS의 과정

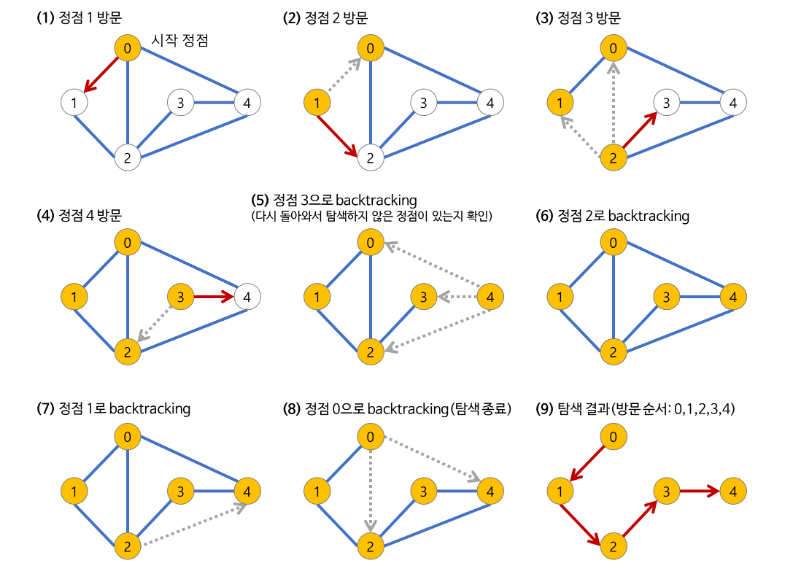
1. a 노드(시작 노드)를 방문한다.
   • 방문한 노드는 방문했다고 표시한다.
2. a와 인접한 노드들을 차례로 순회한다.
   • a와 인접한 노드가 없다면 종료한다.
3. a와 이웃한 노드 b를 방문했다면, a와 인접한 또 다른 노드를 방문하기 전에 b의 이웃 노드들을 전부 방문해야 한다.
   • b를 시작 정점으로 DFS를 다시 시작하여 b의 이웃 노드들을 방문한다.
4. b의 분기를 전부 완벽하게 탐색했다면 다시 a에 인접한 정점들 중에서 아직 방문이 안 된 정점을 찾는다.
   • 즉, b의 분기를 전부 완벽하게 탐색한 뒤에야 a의 다-른 이웃 노드를 방문할 수 있다는 뜻이다.
   • 아직 방문이 안 된 정점이 없으면 종료한다.
   • 있으면 다시 그 정점을 시작 정점으로 DFS를 시작한다.

DFS의 구현

# 재귀활용 구현
def recursive_dfs(v, visited = []):
    visited.append(v) # 시작 정점 방문
    for w in graph[v]:
        if not w in visited: # 방문 하지 않았으면
            visited = recursive_dfs(w, visited)
    return visited

# 스택활용 구현
def iterative_dfs(start_v):
    visited = []
    stack = [start_v]
    while stack:
        v = stack.pop()
        if v not in visited:
            visited.append(v)
            for w in graph[v]:
                stack.append(w)
    return visited

DFS의 시간 복잡도

• DFS는 그래프(정점의 수: N, 간선의 수: E)의 모든 간선을 조회한다.
  - 인접 리스트로 표현된 그래프: O(N+E)
  - 인접 행렬로 표현된 그래프: O(N^2)
• 즉, 그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph) 의 경우 인접 행렬보다 인접 리스트를 사용하는 것이 유리하다.

DFS 관련 백준 문제 Github 링크
백준 DFS 관련 문제