30시간이 날아갔다.
KMP 복습한다고 플래 문제 뒤적거리다가 뭔가 재밌어보여서 풀었는데
한 1시간쯤 풀다보니 정답률 15프로짜리였다..

푼 사람도 보면
c++ 29명 + pypy 4명 ,
푼 사람의 티어는 플래1 2명 + 나 이렇게 3명 제외하고는 다이아~루비, 마스터이다.

그래도 풀었으니 다행이다
포켓몬 빵이나 하나 사먹고 자축하자.

스네이크 게임 성공

시간 제한 메모리 제한 제출 정답 맞힌 사람 정답 비율
2 초 1024 MB 330 47 34 15.455%
문제

알고리즘 원툴 상원이는 첫 프로젝트를 시작했다. 바로 스네이크 게임을 만드는 것이다.

게임에 자신만의 시그니처를 넣고 싶었던 상원이는 특별한 기능을 추가하기로 했다. 원래 뱀은 초록색이지만 게임을 진행하다가 뱀 모양에 숨겨진 특정 모양인 트리거 패턴이 있다면 뱀의 색을 바꾸는 것이다. 하지만 프로젝트에 며칠 밤을 새운 상원이는 도저히 만들 체력이 없다. 여러분이 힘들어하는 상원이를 위해 기능 구현을 도와주도록 하자. 구현해야 할 기능은 뱀 모양에서 트리거 패턴이 몇 개나 있는지 찾는 것이다.

이때 뱀 모양에 회전된 트리거 패턴도 포함해야 한다. 위 뱀 모양의 경우, 보라색으로 표시된 트리거 패턴은 두 번 나타난다. 단, 회전된 모양과는 다른 뒤집힌 모양인 경우는 포함되지 않음에 유의해야 한다.

뱀 모양과 트리거 패턴이 주어졌을 때, 뱀 모양에 있는 트리거 패턴의 개수를 구해보자.

입력
첫 번째 줄에 뱀 모양을 나타내는 점 개수
$N$, 숨겨진 모양을 나타내는 점 개수
$M$이 주어진다.
$(3 \le N, M \le 500\,000)$ 

이어지는
$N$개의 줄에 좌표
$x_i, y_i$가 정수로 주어진다. 뱀 모양은
$(x_i, y_i)$와
$(x_{i+1}, y_{i+1})$을 선분으로 이은 모양이다.
$(-10^9 \le x_i, y_i \le 10^9)$ 

이어지는
$M$개의 줄에 좌표
$x_i, y_i$가 정수로 주어진다. 트리거 패턴은
$(x_i, y_i)$와
$(x_{i+1}, y_{i+1})$을 선분으로 이은 모양이다.
$(-10^9 \le x_i, y_i \le 10^9)$ 

단, 각 모양에 해당하는 선분은 축에 평행하고 연속한 두 선분을 제외하면 서로 겹치지 않는다. 연속한 두 선분은 수직이고 오직 끝 점에서만 만난다.

출력
뱀 모양에 있는 트리거 패턴의 개수를 출력한다.

간단해 보인다. 그냥 뱀을 4방향으로 돌려서 kmp 하면 될 것 같다.
하지만 여기에는 문제가 있는데, 입력값 50만/크기 10^9 라는 점이다.
뱀을 4방향으로 돌리고 역방향까지 계산하면 kmp를 8번씩 해야되는데
얄짤없이 시간초과 터진다.

실제로 처음 문제를 풀때 별거있겠나 싶어서

1. 뱀의 위치를 90도, 180도, 270도, 360도로 각각 회전 시킨후
2. 그 리스트들을 X,Y 로 나눠서([x,y] -> [x],[y])
3. X좌표가 만약 kmp로 통과가 된다면 Y좌표도 KMP로 검사

방식으로 풀었다. 하지만 위와 같이 시간초과가 터졌다.
그래서 시간복잡도를 줄이기 위해 머리 터지게 고민한 결과

• 회전해서 4방향을 계산하는게 중복계산이 아닐까

라는 생각을 하게 되었다.
아니 방향을 돌린것 뿐인데 똑같은 배열에 똑같은 계산을 8번씩 하는게 말이되나?
라는 생각을 했고, 배열의 기준을 x,y좌표가 아닌 진행방향에 두었다.

뱀 게임 시작을 생각해보자.

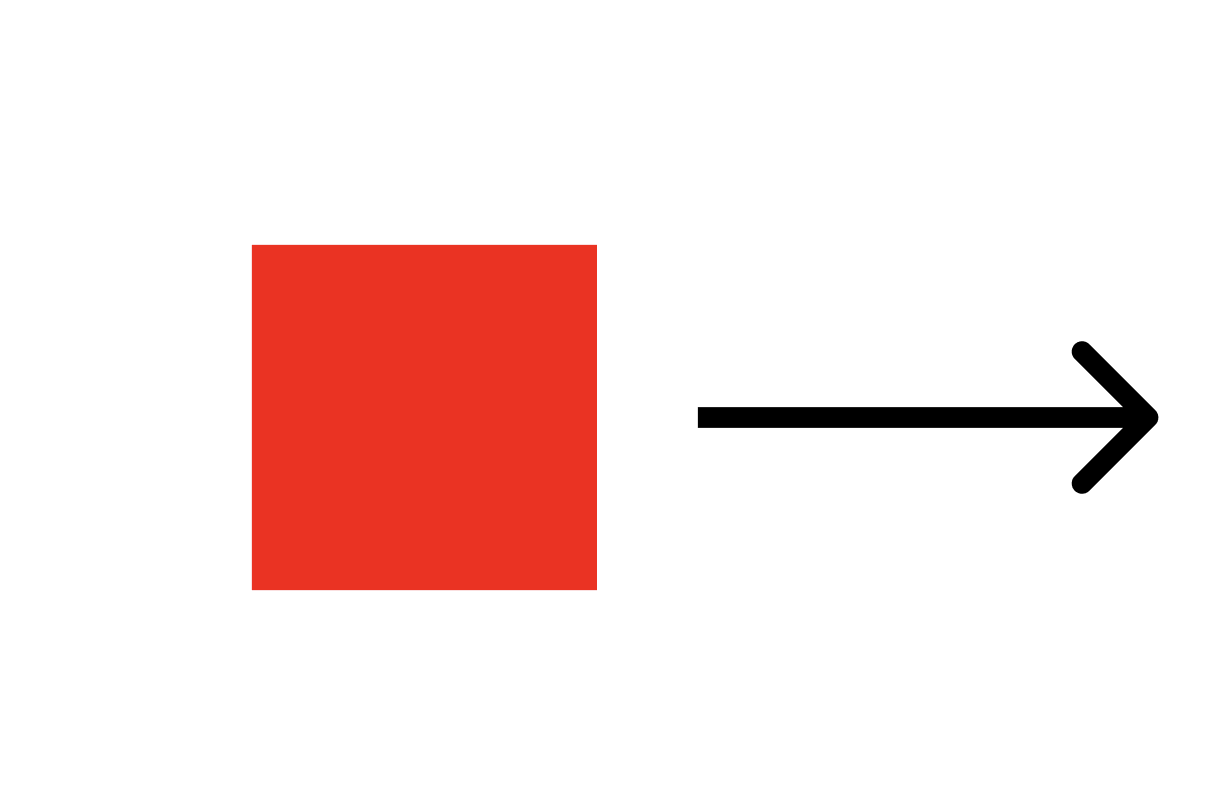
빨간색은 뱀 게임에서 머리를 의미한다.

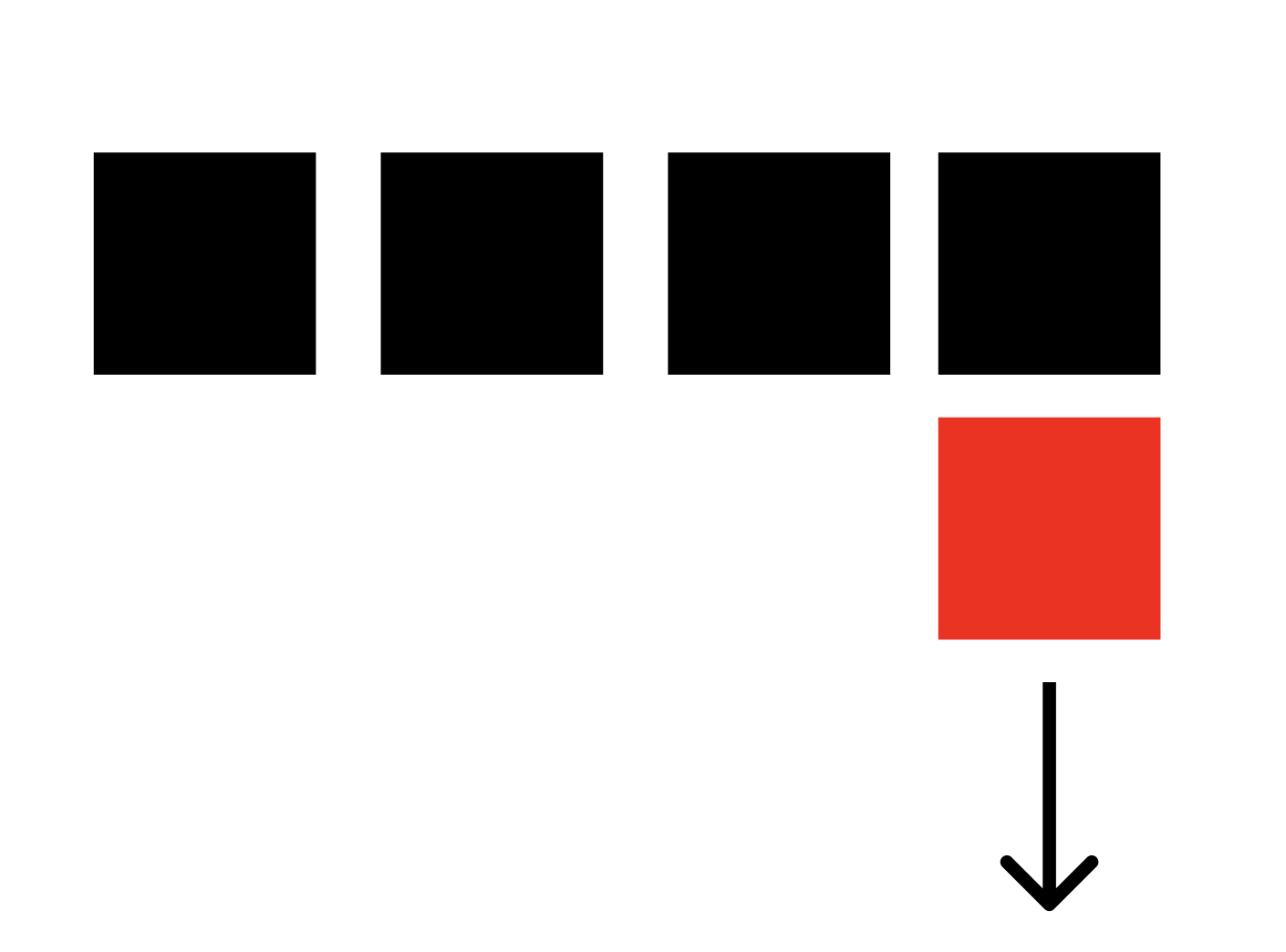
그리고 다음 상황을 보자.
몸의 길이는 4이고, 아래로 갈려고 하고 있다.
그리고, 여기서 중요한 인식의 차이가 있는데, 다음 두가지 방법으로 생각할 수 있다.

• 오른쪽으로 4칸 갔고 밑으로 가려고 하는구나

• 앞으로 4칸 가고 오른쪽으로 방향을 바꾼 후 진행하려고 하는구나

이 둘의 차이점을 알겠는가?
각각을 List로 표현하면 다음과 같다.

오른쪽으로 4칸가고 밑으로 가려고 하는구나 = [[4,0] , [0,-1]]
앞으로 4칸 가고 오른쪽으로 방향을 바꾼 후 진행하려고 하는구나 = [4 , 'R' , 1]

한눈에 파악한 사람도 있을것이고, 이게 뭔가 싶은 사람도 있을것이다.

한번 더 설명을 하자면

첫번째 방법은 진행한 방향을 좌표로 알려주는 것이고([x,y] 만큼 움직였다)
두번째 방법은 진행한 방향을 방향과 길이로 알려주는 것이다.(이정도 움직이고 머리를 왼쪽/오른쪽으로 움직였다)
그래서 위의 예시를 다시한번 살펴보면

[[4,0] , [0,-1]] = x방향으로 4만큼 움직이고, y방향으로 -1만큼 움직임
[4 , 'R' , 1] = 앞으로 4만큼 움직이고, 오른쪽으로 머리를 돌려 1만큼 움직임

이렇게 되면 2차원 평면을 1차원 리스트로 줄일 수 있게 되고, 4방향을 1방향으로 줄일 수 있게 된다. 이론상으로 4배 이상의 계산 압축이 되는 것이다!

또 다른 문제가 발생하는데

그것은 트리거 패턴이 꼭 선 길이를 다 체울 필요는 없다는 것이다.

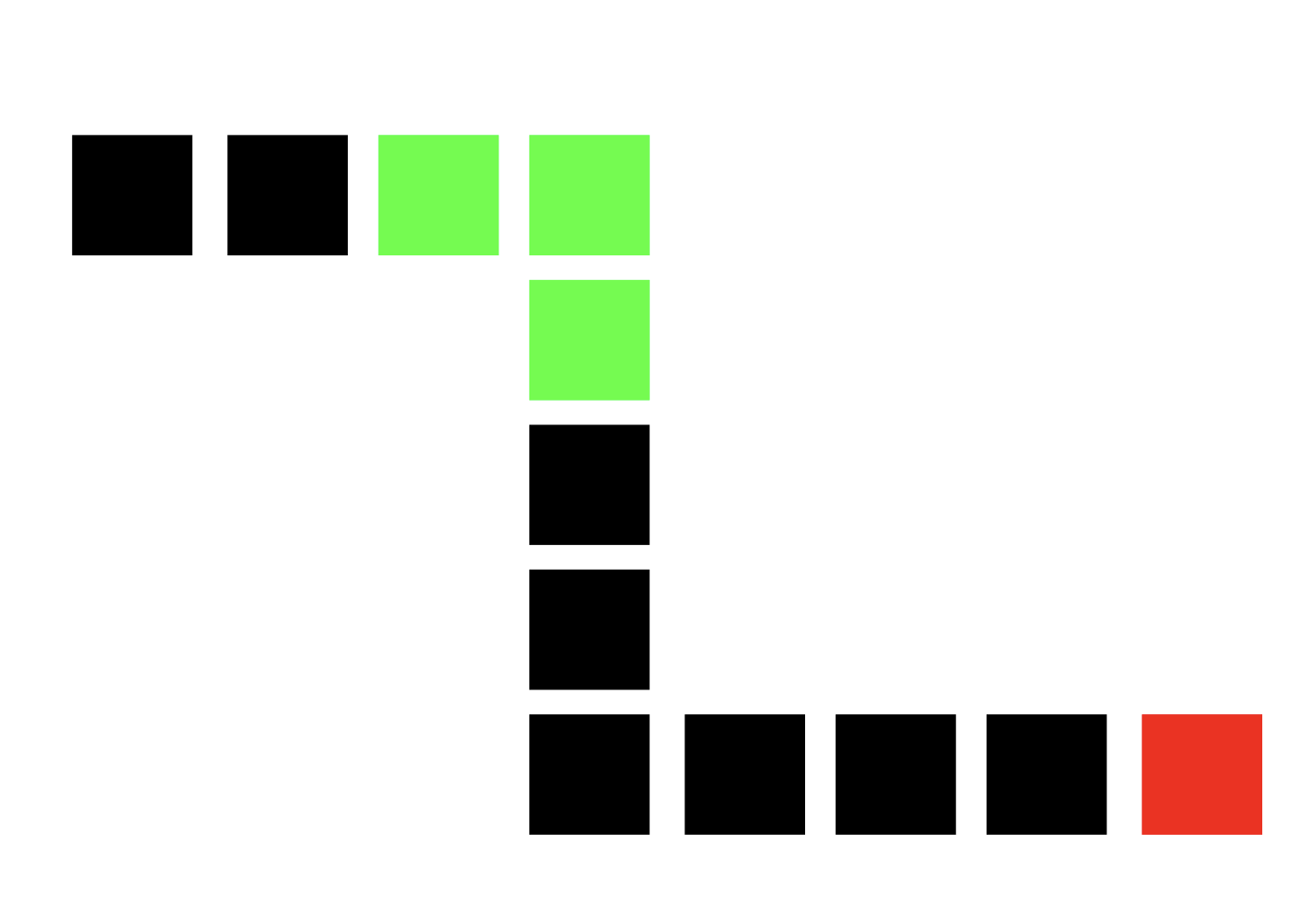
위 사진처럼, 연두색 트리거 패턴이 선을 다 체우지 못하더라도
그저 들어갈 수 있다면 정답으로 인정이 된다.
그러니 위의 경우에는 정답이 2개가 된다는 것이다.

왜 이게 문제가 되냐?
그것은 KMP의 특성 때문에 그렇다.

def fail(a):
    l = len(a)
    cal = [0] * l
    j = 0
    for i in range(1, l):
        while j > 0 and a[i] != a[j]:
            j = cal[j-1]
        
        if a[i] == a[j]:
            j += 1
            cal[i] = j
        else:
            cal[i] = 0
    return cal

위는 내가 사용한 fail 함수이다. (KMP 파이 테이블이라고도 쓴다.)
위를 보면, 같은 숫자일때 j값을 보정해주는것을 알 수 있다.
하지만 이번 문제에서는, 시작/끝 지점의 숫자가 <= , >= 연산을 쓴다는것을 알 수 있다.
그렇기 때문에 이렇게 계산할 경우 KMP에서 배열 중간까지 계산을 하다 j = cal[j] 를 사용할때 j값이 재대로 계산되지 않는 경우가 생긴다.

그래서 내가 생각한 해결법은

• 시작, 끝 지점은 빼고 가운데값만 KMP 연산을 한 후, 나중에 시작, 끝지점을 생각한다.

이다.
여기에는 2가지 이유가 있는데
첫째는 시작값을 기준으로 계산하게 된다면

for k in range(len(본문)):
	for i in range(K , K+len(패턴):

형식으로 사용할 수 밖에 없는데, KMP의 목적인 계산 스킵을 사용 할 수 없게 된다.(결국은 1번 index가 아니라도 판명되어도 KMP 스킵을 사용하지 못하고 2번 index부터 살펴야 함으로)

두번째는 내 실력으로는 예외처리를 할 수가 없다.
생각해보라. 시작/끝값은 상황에 따라 계속 변동하는데(시작값/비교값이 어떠냐에 따라서 계속 경우가 바뀜) 이러한 모든 과정을 예외처리 할 방법이 도무지 생각나지 않는다. 정말 이해가 안되면 직접해보는걸 추천한다. 나도 이걸 무식하게 하려고 하다가 18시간인가 날렸다. 설명하고 싶지만 설명할 방법이 없다.

그렇기 때문에 계속 변동하는 시작/끝값을 때고, 가운데만 계산한 후 ans값을 하나 올릴때, 시작/끝값을 채크하는 식으로 계산하였다.

위의 과정이 정확하게 구현되었다면, 트리거 패턴을 반대로 뒤집어서 한번 더 돌리고, 두 값을 더하면 답이 나온다. 하지만 트리거 패턴을 뒤집었을때 기존 트리거 패턴과 값이 같다면 할 필요가 없다.

내 자신의 나약함이 너무나도 절실하게 느껴지는 문제였다.
이때까지 레퍼런스/블로그 참고를 너무 많이 했다는 느낌이 들었다.
점수에만 급급해 기본에 충실하지 못한게 아닐까? 라는 생각도 들었다.
평소의 태도를 반성하기에 30시간은 그렇게 긴 시간이 아닌거 같다. 좀더 부지런해지자.

아니 근데 이거 대회문제인거같은데 푸는사람들은 도대체 어떤 사람인지 궁금하다.
뇌가 3개씩달렸나?

그리고 솔브닥 1프로대 진입한거 자랑