
분할정복
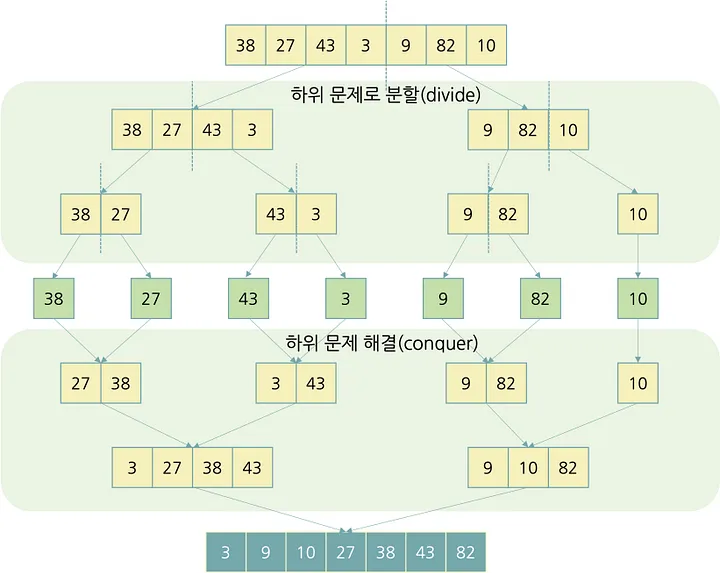
분할정복을 사용한 merge - sort - algorithm
찾아보면서도 정말 애매모호하고 두루뭉실하게 설명이 되어 있었다.
분할정복이란 해결할 수 없는 문제를 작은 문제로 분할하여 문제를 해결하는 방법이나 알고리즘이다.(위키)
분할정복의 보통 제귀함수를 통해서 자연스럽게 구현이 된다.
제귀함수 중 피보나치 수를 예로 들어보자.
Fn의 값을 구하려고 한다.
하지만Fn은 커녕 Fn-1, Fn-2..... 심지어 피보나치 수를 처음 접하는 사람이라면
F5조차 계산하기 힘들 것이다.
그래서 우리는 이 풀기힘든 문제를 작게 나눠서 계산하게 되었다.
Fn = Fn-1 + Fn-2
짜잔! 큰 문제를 정말 작게 잘라서, 계산 중 한 과정만을 나타내게 되었다.
그리고 운이 좋게도 이 과정을 반복하다보면 F1부터 시간만 충분하다면 Fn(n = 엄청큰수)도 구할 수 있다!
실제로 def를 통해서 함수를 불러오는 형식이 아닌, 단순 for 반복문을 통해서 계산을 돌리는 경우
100000번째 피보나치 수를 찾는것 따위 누르자마자 답이 튀어나온다.
a = int(input())
f1 = 0
f2 = 1
f3 = 1
for i in range(a-2):
f1 = f2 + f3
f3 = f2
f2 = f1
if a == 1:
f1 = 1
if a == 2:
f1 =1
print(f1)정렬
여러 key를 항목의 대소 관계에 따라 데이터 집합을 일정한 순서로 바꾸어 늘여놓는 작업을 말한다.
말로만 써놓고 보면 간단하지만, 종류도 많고 내용도 많고 분량도 많다.
무려 78page가 정렬만 설명하고 있다.
정렬 중 단순 삽입정렬, 셸 정렬은 스킵한다. 도저히 다 공부할 수도 없을 뿐더러 우선순위에 밀린다.
간단하게 적으면 단순 삽입정렬은 arr[n]을 자신의 앞쪽 숫자들과 비교해서 자신의 자리를 찾아가는것이고,
셸정렬은 버블정렬의 단점인 '먼거리를 이동할때 시간이 오래걸린다'는 단점을 해결하기 위해 여러개의 리스트(일정 간격씩 떨어진 데이터들)를 만들어 정렬하는 방식이다.
버블 정렬
밑에 있던 원소가 거품이 올라오는것처럼 떠오른다고 해서 붙여진 이름이다.(위키)
가장 간단하지만 시간복잡도가 매우 크다(n^2).
코드는 쉽다.
def bubbleSort(x):
length = len(x)-1
for i in range(length):
for j in range(length-i):
if x[j] > x[j+1]:
x[j], x[j+1] = x[j+1], x[j]
return x코드를 자세히 살펴보자.
만약 앞의 코드가 뒤쪽코드보다 값이 크다면
if x[j] > x[j+1]:앞과 뒤의 값을 바꾼다.
x[j], x[j+1] = x[j+1], x[j]간단하다. 그렇기 때문에 무식하고 단순하다. 브루탈포스가 생각난다.
이렇게 단순하기 때문에 약간의 조건만 추가해 줘도 효율을 엄청나게 끌어올릴 수 있다.
- 원소가 교환이 이루어지지 않을때 바로 코드를 끝내는 방법(이미 정렬이 끝났다고 판단.)
- 앞쪽의 원소가 교환되지 않는다면, 다음 루프때 정렬된 부분은 계산하지 않는 방법(정렬된 곳은 반복정렬x)
- 뒤에서 앞으로 정렬 한 후, 다음번 루프는 앞에서 뒤로, 그다음루프는 다시 뒤에서 앞으로 정렬하는 방법(큰 숫자가 앞에 있을때 비효율적이기 때문에. 가장 큰 수가 가장 앞에 있다고 생각해보자.)
삽입정렬
insertion sort 말 그대로 데이터를 끼워 넣는다는 소리다.
다음 데이터를 보자.
6 4 1 7 3 9 8
이 데이터를 오름차순 정렬을 하려고 한다. 우선 두번째 4를 주목해보자.
4를 기준으로 왼쪽의 데이터를 나열해 보면
6
하나가 있다.
4는 6보다 작음으로 6의 왼쪽에 '삽입'한다.
전체데이터를 다시 살펴보면
4 6 1 7 3 9 8 이 된다.
이제 세번째 데이터인 1을 보자.
1 왼쪽의 데이터를 보게되면
4 6
이 된다.
1은 4와 6보다 작으니 4 왼쪽에 삽입한다.
이후 전체 데이터를 다시 살펴보면
1 4 6 7 3 9 8 이 된다.
이렇게 하나하나 비교하며 삽입하다보면 금방 정렬이 끝나고,
결과는 1 3 4 6 7 8 9가 된다.
결국에 하나하나 다 살펴보면서 넣어야 하기 때문에 시간복잡도가 엄청 크다(n^2)
퀵정렬
빠른 정렬이다.
https://velog.io/@wndudrla1011/interview-algorithm-sort-quick#-%ED%80%B5-%EC%A0%95%EB%A0%AC%EC%9D%B4-%EB%B9%A0%EB%A5%B8-%EC%9D%B4%EC%9C%A0
정렬과정을 적기에는 양이 너무나도 많기 때문에 링크로 때움
퀵정렬 장점
- 정렬되지 않은 데이터의 정렬이 엄청나게 빠르다.
- 메모리 소모가 엄청 적다.
퀵정렬 단점
- 정렬된 데이터는 엄청나게 느려진다 (On^2) (이건 정렬되는 방식만 봐도 알 수 있는데, 피벗값이 두드러지지않고 오름차순/내림차순으로 정렬되어 있으면 전체 정렬을 왔다갔다하면서 엄청나게 비효율적으로 정렬된다.)
- 재귀를 사용하지 못하는 환경에서 구현이 엄청나게 복잡하다.
(딱봐도 똑같은거 반복 반복이다)
퀵정렬이 빠른 이유
-> 큰 숫자는 오른쪽으로(오름차순에 가깝게), 작은숫자는 왼쪽으로 보내면서
숫자가 찾아가야할 자리에 근접하게 배치시키며 정렬하기 때문에 엄청 빠르다.
퀵정렬을 많이 쓰는 이유?
-> 메모리 참조가 지역화 되어 있어서 캐시의 히트율이 높다. 라고 한다....
뭔말인지 모르겠으니 한번 알아보자.
캐시 메모리 라는 것이 있다.
컴퓨터에서 cpu가 메모리 참조를 할때, ram에서 메모리 참조를 하는게 시간이 오래 걸리기 때문에, 중간에 보급 창고 비슷한걸 만들어서 메모리 참조를 하는 시간을 줄이는데, 이것을 캐시 메모리 라고 한다.
이때 캐시 메모리에서 참조할 데이터의 밀집도가 높은걸 지역화가 된다고 한다.
창고에서 물건을 꺼낼때 한곳에 모여있으면 시간이 절약되는것과 비슷하다고 한다.
그리고 캐시의 히트율이 높아진다는 것은, 필요한 정보를 캐시 메모리에서 찾아냈다는 것을 의미하고, 주기억 장치까지 찾으러가는 시간이 절약된다는 것임으로,
연산의 속도가 더욱 빨라진다는 것을 의미한다.
정리
퀵정렬은 컴퓨터 아키텍쳐에서 효율적으로 작동하기 때문에
메모리의 지역화가 잘 일어나고,
캐시의 히트율이 높아져서 계산속도가 빠르다
