크래프톤정글3주차 - 다이나믹 프로그래밍 ( + 딕셔너리/비트마스킹)

한 6시간 정도를 한참 해맸다. 진짜 뭔소린지도 모르겠고 파이썬 자료형도 다 익히지 못해서 이리저리 치이는 중이다.
지금 느끼는게 작년에 한달 반짝 해서 백준 골드 찍었던 실력이 밑바닥을 보이는 느낌이다.

그래서 1~2주차때는 그나마 할만하기도 했고 dfs/bfs정도까지는 복습을 하지 않아도 머리에 확실히 기억이 남을 것 같으니 공부일지에 적지는 않았지만, 마지막 주차의 다이나믹 프로그래밍/그리디 등의 알고리즘 풀이는 막히면 혼자 고민하기 보다는 답안을 본 후, 그 해답을 뜯어보는 글을 적을 것 같다.

그리고 한가지 부탁이
의사코드를 재대로 배운것이 아닌 날라리(독학)공부를 했기 때문에 정확하지 않을 수 있지만
문맥상 이런느낌이구나~ 라는것만 이해했으면 좋겠다.

다이나믹 프로그래밍

다이나믹 프로그래밍은 신성 로마제국과도 같다.

• 신성하지도 않고
• 로마도 아니고
• 제국도 아닌

신성 로마제국과도 같이

• 다이나믹하지도 않고(동적이지 않음)
• 프로그래밍도 아니다.(풀이 방법임)

왜 그런지는 정말 유명한 이야기인데, 연구실에서 다이나믹 프로그래밍을 연구하면서
단순히 연구비를 많이 받기위해 이름을 멋지게 짓고 싶었다고 한다.

이렇게 적어놓으면 상당히 속물적인 사람으로 보이겠지만,
사실 리처드 벨만 교수가 연구하던 시대상이 주변분위기가 수학공부를 방해했다고 한다.
그래서 별 문제없이 방법을 발표하기위해서 이름을 그렇게 지었다고 한다.

그래서 우리는 이러한 사실에서 알 수 있듯이,
다른 알고리즘과는 다르게 이름에 매몰되면 안된다.

작동원리

다이나믹 프로그래밍은 크게 2가지 원리로 작동한다.

• top-down
• bottom-up

이 2가지의 구별 방법은 간단하다.
우리가 풀려고 하는 문제를 큰 크기에서 작은 크기로 나누는지
아니면 작은 크기의 문제를 해결하면서 합쳐나가 전체 문제를 해결할지 이다.

감이 잘 안올것이다.
근데 이건 예시 1개만 봐도 바로 이해할 수 있다.
하지만 코드가 비슷해서 정신 바짝차리고 10분만 읽어면 좋을 것 같다.

top - down 방식

fibo(1) = 1
fibo(2) = 1
if i > 2:
	fibo(n)



def fibo(n):
	return fibo(n-1) + fibo(n-2)

위는 실제로 작동하는 코드는 아니며, 의사코드 형식으로 구조만 나타낸 것이다.
코드를 뜯어보면
피보나치 수열은 n = 1 일때 1, n = 2 일때 1을 출력한다.
하지만 n = 3 부터, fibo(3) = fibo(2) + fibo(1) 가 된다.

즉, fibo(n) = fibo(n-1) + fibo(n-2)
= (fibo(n-2) + fibo(n-3)) + (fibo(n-3) + fibo(n-4)
= ....
이렇게 쭉쭉 내려갈 것이다.

fibo(n) = fibo(n-1) + fibo(n-2) 이니,
fibo(n-1) = fibo(n-2) + fibo(n-3)이고
이 fibo(n-1)을 위 식에 대입하면

fibo(n) = (fibo(n-2) + fibo(n-3)) + fibo(n-2)
가 되고 이걸 반복한다는 소리다.

즉

이 식은 마지막에 결국
a x fibo(2) + b x fibo(1) 가 된다는 것을 의미한다.
하지만 우리는 이미
fibo(2) = 1 , fibo(1) = 1 이라는 '연산'을 미리 해 놓았지 않은가?
그렇기 때문에 추가적인 연산을 하지 않고, a와 b값을 알기만 하면 바로 정답을 구할 수 있다는 소리다.

이렇게 과거의 연산이 미래의 연산에 참조가 되는 것을 memoization이라고 한다.

이렇게 top-down 형식은 장점과 단점이 명확하다.

장점

• 코딩이 어어엄청 쉽다.(비교적)

단점

• 피보나치 수 1000이 4.346E+208이라는 숫자가 나온다.
  E+208이 뭔소리냐고?
  10의 208제곱이라는 소리다.
  이런숫자를 담을려고 하면 메모리가 비명을 지르며 오버플로우가 정말 잘 일어난다.

bottom - up 방식

fibo(1) = 1
fibo(2) = 1
if n > 2 : 
	for i in range(n-2):
		fibo(n) = fibo(n-1) + fibo(n-2)
        fibo(n-2) = fibo(n-1)
        fibo(n-1) = fibo(n-2)

마찬가지로 의사코드를 적어봤다.

위 코드가 올바르게 적혀서 작동을 하게 된다면
fibo(3) = fibo(2) + fibo(1)
fibo(4) = fibo(3) + fibo(2) ....

이렇게 주루루룩 연산이 될 것이다.
그럼 우리가 fibo(30)까지 연산을 했을때,
리스트 형식인 fibo에 1~30까지의 연산 결과가 모조리 저장되어 있을 것이다.
이렇게 계산 결과가 저장되어 있는것을 표에 적어놓는다고 해서 tabulation이라고 한다.

++ 설명이 짧아서 보충

점화식 A[i][j] = A[i-1][j-t]+S[i]라는 식이 있다고 하자.
t = 1이라고 할 때,
A[10][10]을 구하려고 하면
A[9][9]+S[9]를 알아야 하고, 이를 알기 위해서는
A[8][8] + S[8]을 알아야하고... 할것이다.

그래서 계산결과를 미리 2차원 배열에 기록하면서 나아간다고 보면 된다.

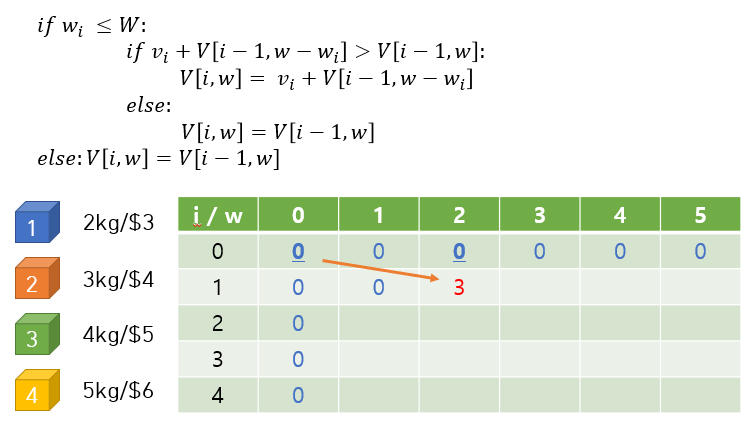
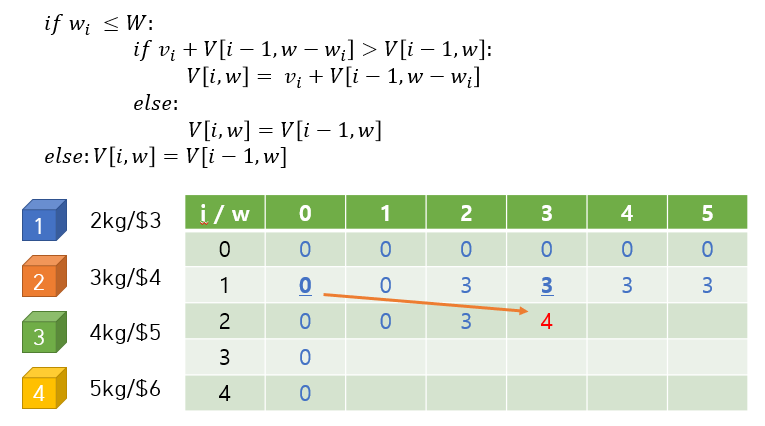
(V[i][j] = max(V[i-1][j],V[i-1]j-물건의 무게[i]] + 물건의가치[i])
knapsack 배낭에 물건넣기의 점화식

이 사진처럼 말이다.
V[2][3]을 구하기 위해서는 미리 V[1][0]과 V[1][3]을 계산 해 놔야 하는데,
[0][0]부터 쭉 계산을 하며 표를 체워 놨기 때문에 V[2][3]을 계산할때
표에서 '참고'만 하면 된다는 소리다!

즉

이러한 점화식의 계산은 [0][0]부터 순차적으로 계산을 하며 표를 체워나갈 수 있다.
그렇기 때문에 추가적인 연산을 하지 않고, 이전값을 참고만 하면 바로 정답을 구할 수 있다는 소리다.

이렇게 과거의 연산이 미래의 연산에 참조가 되는 것을 tabulation이라고 한다.

top-down과 마찬가지로 장/단점이 명확하다.

장점

• 메모리도 엄청 적게 먹고 계산속도가 장난아니다.
  구조만 봐도 top-down형식은 재귀형식이라서 함수 호출을 계속 해대는데,
  이런 과정 때문에 속도도 느리고 메모리도 많이 잡아먹는다.

하지만 bottom-up은?
while이나 for문을 돌리기 때문에 성능이 무지막지하게 뛰어나다.

단점

• 코딩이 어어엄청 어렵다.(비교적)

적다보니까 정말 할만한것같다.
근데 뭐때문에 이렇게 밑밥깔면서 글을 적는것일까?
문제는 비트마스킹이다.

비트 필드

일단 비트 필드를 이해할려면 비트 연산을 이해해야 한다. 여기에서는 설명 안하니 다른 블로그를 찾아보는걸 추천한다.

어쨌든 비트를 저장한다고 생각해보자.
4비트짜리 배열구조를 보자.

0000

여기서 왼쪽부터 인덱스를 붙여준다고 '생각' 해보자. (실제로 붙이는게 아니니까 오해 하면 안된다.)

1234
0000

여기서, 1번 밑에 있는 비트가 1이 된다고 생각해보자.

1234
1000

여기서 감이 좀 오는가?

어떤 장소를 방문하는지에 대한 문제를 예시로 들면
0을 방문하지 않은곳, 1을 방문한 곳이라고 '가정' 해보면

1000

이 4비트짜리 코드는
1번도시를 방문했다는 것을 알려주는 것이다.

진짜 이걸 보고 뒷통수를 빠따로 맞는듯한 충격을 느꼈다.
우리가 평소에 쓰는 list[]는 몇개 쓸때는 상관없지만 배열이 10만개쯤되면 메모리가 힘들어하는게 눈에 보인다. 하지만 저 비트마스킹은 '구조만 잘 짜면' 거의 자원을 들이지 않고(시간/메모리 모두 포함)연산을 자유롭게 할 수 있는 것이다.


비트필드의 장/단점

장점

• 장난아니게 빠르다.
• 코드가 짧다.
• 메모리 사용량이 엄청나게 적다.

단점

• 실수 한번하면 코드가 완전히 엉켜버린다.
• 코딩 난이도가 높다.
• 비트 제한이 있어서 너무 길게는 못한다.

완벽해보이던 비트필드도 결국 난이도의 벽이 있는 것이었다.
쉬우면 누구나 다 쓰지 당연한 결과긴 하다.

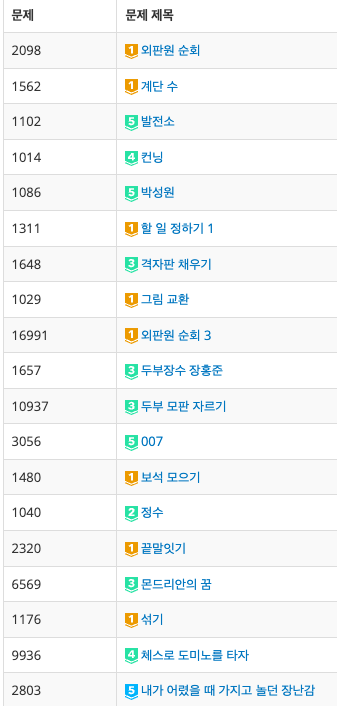
실제로 백준에 비트필드를 이용한 다이나믹 프로그래밍 관련 예제들의 난이도를 보면 저따구다.
최소 골드1에서 플레~다이아는 그냥 페이지마다 꽉꽉 차 있으며 뒤쪽으로 가면 루비 문제도 나온다.
그렇기 때문에 비트필드에 대한 개념은 확실하게 잡고 가는것이 좋다고 생각한다.

백준 2098 외판원 순회

https://www.acmicpc.net/problem/2098
(백준 사이트)

https://velog.io/@e_juhee/python-%EB%B0%B1%EC%A4%80-2098-%EC%99%B8%ED%8C%90%EC%9B%90-%EC%88%9C%ED%9A%8C-DP-%EB%B9%84%ED%8A%B8%EB%A7%88%EC%8A%A4%ED%82%B9-lso2bk58
(이번 글에서 쓰는 코드의 출처)

이 프로그래머 분은 백준 검색할때 정말 자주 보이는 분인것 같다.
코드도 엄청 깔끔하고 구조도 잘 짜여 있어서 도움이 엄청 된다.

import sys
N = int(input())
world = []
for _ in range(N):
    world.append(list(map(int, sys.stdin.readline().split())))

dp = {}


def DFS(now, visited):
    # 모든 도시를 방문한 경우
    if visited == (1 << N) - 1:
        # 다시 출발 도시로 갈 수 있는 경우 출발 도시까지의 비용 반환
        if world[now][0]:
            return world[now][0]
        else:
            # 갈 수 없는 경우 무한대 반환 (이 경로가 최소비용으로 채택되지 않게)
            return int(1e9)

    # 이전에 계산된 경우 결과 반환
    if (now, visited) in dp:
        return dp[(now, visited)] # now까지 방문한 최소 비용

    min_cost = int(1e9)
    for next in range(1, N):
        # 비용이 0이어서 갈 수 없거나, 이미 방문한 루트면 무시
        if world[now][next] == 0 or visited & (1 << next):
            continue
        cost = DFS(next, visited | (1 << next)) + world[now][next]
        min_cost = min(cost, min_cost)

    dp[(now, visited)] = min_cost  # 현재도시까지 방문한 경우 중에서 최소 비용이 드는 루트의 비용 저장
    return min_cost  # 현재도시까지 방문하는 비용 리턴


print(DFS(0, 1))  # now: 0번째 도시부터 방문, visited: 0번째 도시 방문 처리

코드는 이렇게 된다.
우선 우리가 살펴보아야 할 곳은 크게 2가지 이다.

• 첫번째는 딕셔너리의 사용
• 두번째는 비트마스킹의 사용

기존의 코딩 방식은 그냥 list만 썼다. 가끔 중복 안되면 set으로 잠깐 바꾸는게 전부였다. 그러다 보니 list의 값이 많아도 그냥 무식하게 list 안에 원하는 값을 검색해서 나오는 index값을 가지고 다시 print하는 바보같은 짓을 했던 것이다.

하지만 딕셔너리는

	dp[(now, visited)] = min_cost

키값을 찾아서 바로 데이터를 끄집어낸다.
이건 사실 대단한건 아니고 코딩습관의 반성과 잊지않기 위해서 적은것이다.

이제 중요한 비트마스킹을 봐야 한다.

if world[now][next] == 0 or visited & (1 << next):
            continue
        cost = DFS(next, visited | (1 << next)) + world[now][next]
        min_cost = min(cost, min_cost)

visited는 도시 개수만큼의 크기를 가진 비트필드이다. 문제에서 2<=N<=16이라고 했으니 16비트 조건이 충족된다.

visited & (1 << next)

이 코드가 의미하는것은 1을 next번 왼쪽으로 밀어서 visited에 있는지 확인하는것이다.
visited에서 오른쪽에서 next번째가 1이 되어 있다면 and연산에 의해 True가 나올 것이고,
0이라면 False가 나올 것이다.

설명을 추가하자면 다음과 같다.(index는 설명을 위해 추가)

9 8 7 6 5 4 3 2 1
0 0 1 0 1 1 0 0 1 

0 0 0 0 0 0 0 0 1

위가 visited이고(9~1의 숫자는 index라고 생각하자.)
밑은 1이다.
여기서 1을 next(5라고 가정하자)만큼 왼쪽으로 옮기면

9 8 7 6 5 4 3 2 1
0 0 1 0 1 1 0 0 1 

0 0 0 0 1 0 0 0 0

이 된다.

여기서 &연산(AND) 연산을 하게 되면True가 나오게 된다.(비교하려는 next의 위/아래 모두 1이니까)

이렇게 도시를 방문 했는지 안했는지 확인 할 수 있다.

다음은 도시를 방문했다고 마크를 찍는 것이다.

        cost = DFS(next, visited | (1 << next)) + world[now][next]

이 구문을 살펴보자.
DFS는 우리가 쓰는 함수니까 넘어가고 중요한건 그 다음이다.

         visited | (1 << next)

다른거 다 짤라먹고 이것만 쓰는 이유는 이 구문만 가지고 우리가 어디 도시에 방문했는지 채크를 할 수 있기 때문이다.

9 8 7 6 5 4 3 2 1
0 0 1 0 1 1 0 0 1 

0 0 0 1 0 0 0 0 0

6번 도시에 방문해서 밑의 비트가 6에서 1이 되었다고 생각하자.

비트연산자에서 |연산은 or을 의미하고, 이미 방문을 했으면 애초부터 위에서 막았을 것임으로
연산 후에는 다음과 같은 결과가 나올 것이다

9 8 7 6 5 4 3 2 1
0 0 1 1 1 1 0 0 1 

놀랍지 않은가?
그냥 코드 한줄 한줄 넣으니까 visit[[False] for _ in range(N)]이니 뭐니 별별짓을 하지 않아도 한방에 채크가 되는것이다...!!!!

결론

아마 내 생각으로는 비트필드가 3주차 알고리즘 과정 중에서 가장 어려운 부분이 될 것 같다.
이 뒤에 최장 공통 부분 문자열이라고 플레티넘 문제가 하나 있기는 한데 그건 다 하고 시간 남을때 하는것 같다.

당장 이번 알고리즘 다 풀고나면 c언어/포인터 csapp 책 읽기 등을 해야되는데
얼마나 더 힘들어질지 감도 안잡힌다.

열심히 살아남아야 한다.

라고 생각했었다..