이 글을 읽기 전에

https://dev-game-standalone.tistory.com/92
이 글은 위 링크의 글과 clrs알고리즘책을 읽고 그대로 쓴 것에 가깝다.
더 자세한 설명과 풀이를 보고 싶다면 링크의 글을 읽는것이 도움이 많이 될 것이다.

RB트리, 즉 트리의 노드 색깔을 빨간색/검은색으로 나눴다는 거다.

RB트리의 규칙을 살펴보자.

• 노드는 레드 혹은 블랙 중의 하나이다.
• 루트 노드는 블랙이다.
• 모든 리프 노드들(NIL)은 블랙이다.
• 레드 노드의 자식노드 양쪽은 언제나 모두 블랙이다. (즉, 레드 노드는 연달아 나타날 수 없으며, 블랙 노드만이 레드 노드의 부모 노드가 될 수 있다)
• 어떤 노드로부터 시작되어 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 리프 노드를 제외하면 모두 같은 개수의 블랙 노드가 있다.

여기서 제일 중요하게 볼 규칙은 5번이다.
이게 왜 중요하냐면

2진탐색에서 특정 값의 레벨이 너무 높으면(특정 리프를 찾는데 너무 많은 노드를 건너야 되면) 자료를 찾는데 걸리는 시간이 log n 을 훨씬 넘을 수도 있기 때문이다.
그렇기 때문에 RB트리는 모든 리프의 값을 찾는데 걸리는 시간이 균일해지게
자동으로 트리를 정리하는 트리라고 생각하면 편하다.

하나하나 손으로 계산 하는게 아니라
코드 하나만 잘짜놓으면 자동화가 완성된다는 뜻이다!

그렇다면 우리는 뭘 알아야 할까?
크게 2개를 알아보면 된다.

바로 insert 와 delete 다.
insert 는 말 그대로 트리에 값을 집어넣는다는 것이고
delete 도 트리의 값을 없앤다는 뜻이다.

시작전 트리의 기본 지식

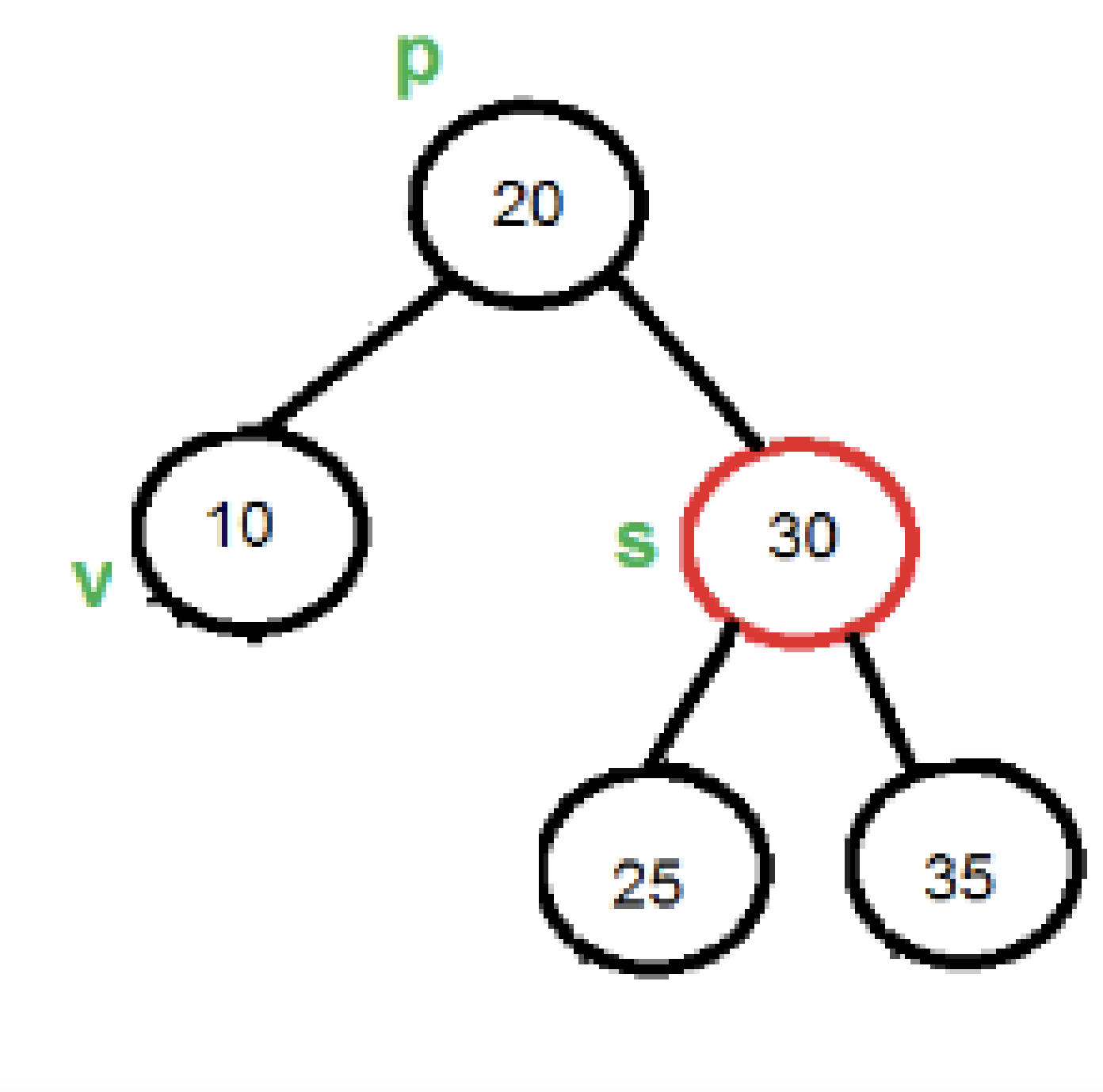
진짜 중요하니까 사진 엄청 크게 넣었다.
한번 스으읔 보고 이해됐어! 이러고 넘어가지 말고

진짜 중요하니까 정독 3번 하길 권장한다.

너무나도 중요하다. 계속 중요하다고 말하는데
이거 안되면 나중에 개념 설명할때 계속 햇깔리니까 꼭 보도록 하자.

노드 10번 기준으로 설명한다.

• 자신의 위에 있는 노드를 '부모 노드' 라고 한다.

• 자신의 옆에 있는 노드, 즉 같은 부모를 가지고 있는 노드를 '형제 노드'라고 한다.

• 형제 노드의 자식들 '조카 노드' 라고 부른다.

• 내 부모와 부모가 같고, 내 부모가 아닌 노드를 '삼촌노드' 라고 한다.(드립이 아니라 진짜 uncle node라고 부른다)

• 삼촌노드는 25 기준으로 10이다.

한국사람이면 4촌 까지는 익숙할것이다.
삼촌/조카 정도는 알지 않는가?
혹시 외국인이라면 주변에 있는 한국사람들한테 물어보던가 하자.
위의 개념이 '정확하게' 숙지 되었으면 다음으로 가자.

++그리고 뭔 부모의 부모 이딴 설명을 쓰냐고 화내는 사람 분명히 있을껀데
나중에 프로젝트 할때 코딩을 그렇게 해야되서 그렇다. 그래프 fix 할때도 이런식으로 써야되니까
이해해줬으면 한다.

insert

트리에 값을 집어넣을때는 항상 red만 넣어야 된다!!
이건 규칙이니까 꼭 기억하자.
그리고 RB트리는 왠만하면 케이스별로 어떻게 해야되는지 암기를 하고
이게 왜 그런가는 조상 노드에서 내려올때
black 노드를 몇개 지나게 되는가? 를 생각해보면 된다.

insert - 1 ) 처음 넣는 경우

2번째 규칙 - 트리의 루트는 black이다.
를 지켜야 하기 때문에 처음넣는 노드는 black으로 만들면 된다.

insert - 2 ) 부모가 black인 경우

규칙에 위배되는것이 없기때문에
편안하게 넣으면 된다.

insert - 3 ) 부모가 red인 경우

지금부터 rb트리의 진짜 문제가 시작된다.
부모가 red인 경우 자식도 red가 되면 red-red 현상이 발생하게 되며
4번 규칙에 위배가 되기 때문이다.
이제 하나하나 경우를 따져보자.

insert - 3-1 ) 부모/삼촌 노드가 red 인 경우

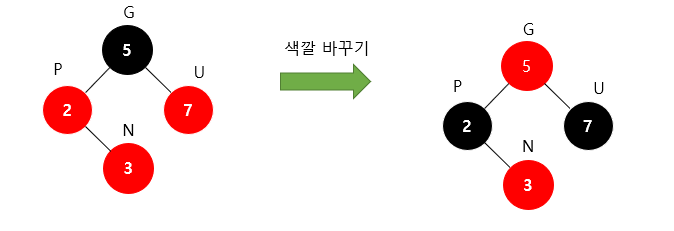
G의 색깔을 빨간색 , P와 U의 색깔을 검은색으로 바꾼다.

insert - 3-2 ) 부모가 red/ 삼촌이 black 인 경우

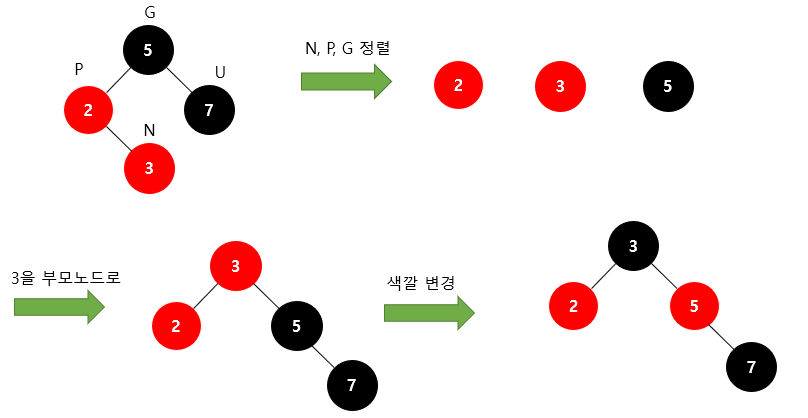
N , P , G 를 크기순으로 정렬을 한 후, 가운데 숫자를 부모 노드로 만든다.
그렇게 되면 2 , 3 , 5 중 3이 중간값이니 부모 노드가 되고, 2 와 5 는 자식 노드가 된다.
이때 부모노드를 검은색으로 바꾸면 된다.
여기서 3이 부모노드니까 검은색으로 바꾸고,
그렇게 되면 7로 갈때 검은색을 3개 지나야 하니
5를 빨간색으로 바꿔준다.

다시한번 정리하면

부모가 red/삼촌이 black인 경우

• N , P , G 를 정렬해 가운데 노드를 부모로 만든다.
• 그렇게 되면 세 노드 중 2개는 red 가 될 건데, 부모 노드를 검은색으로 칠하고,
  나머지 검은색을 빨간색으로 바꾸면 된다.

위 세 케이스를 '정확하게' 암기하고 있다면 삽입은 그냥 저 공식 그대로 쓰면 된다.

delete

트리에서 값을 제거할때 빨간색을 빼는거면 그냥 편안하게 빼면 된다.
아무런 조건도 어기지 않는다.(어차피 Null이 검은색이라 상관없다.)

하지만 검은색을 삭제 했을때는 문제가 발생하게 되는데,
부모 노드인 빨간색에서 검은색 자식 노드의 Null 값으로 접근한다고 생각해 보자.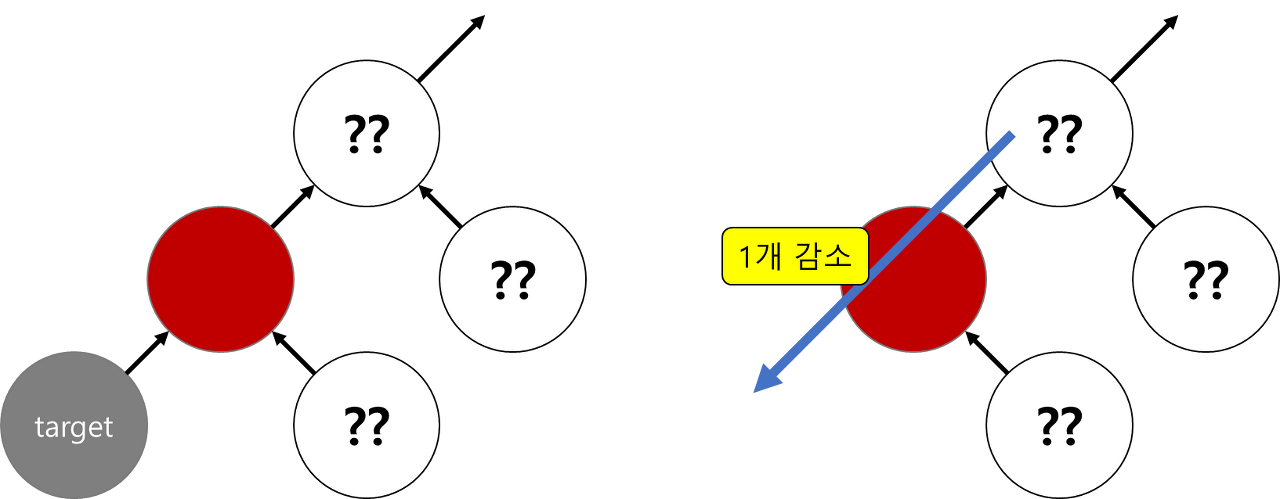
원래대로라면

• 빨간색 부모 노드 -> 검은색 자식 노드 -> 검은색 Null 노드
  => 총 2번의 검은색 노드를 지나야 한다.

하지만 검은색 자식 노드를 삭제하게 되면

• 빨간색 부모 노드 -> 검은색 Null 노드
  => 총 1번의 검은색 노드를 지나야 한다.

위에 적었던 rb트리 조건 5번 을 보자.

• 어떤 노드로부터 시작되어 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 리프 노드를 제외하면 모두 같은 개수의 블랙 노드가 있다.

5번 규칙에 위배가 되는것을 확인할 수 있다.
그래서 rb트리에서 삭제는 '검은색 노드'를 삭제할때만 따져보면 된다.

이 4가지 케이스 + insert 2가지만 정확하게 보면 rb트리는 구현이 된다고 보면 된다.

• 이해가 안되면 일단 외우면 된다. 특정한 상황일때 저 케이스들 쓰면 다 풀린다.

delete - 1 ) 형제가 red

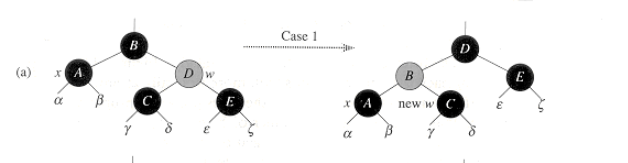
첫번째 case이다.
자신과 부모, 조카는 모두 black이고, 형제는 red 이다.

이 case는 문제 해결을 위한 것이 아닌, 2~4번 case를 사용하기 위해서 상태 변화를 시키는 것이라고 보면 된다.

실제로 색깔 변경 + rotation을 해도 왼쪽, 오른쪽의 black 노드 개수가 달라지는게 없다.
즉 저런 형태라면 정상적인 트리에 case1을 적용시켜도 아무런 문제가 없다는 소리다.

그렇기 때문에 case1은 트리의 문제를 해결하기 위한 '전처리'단계라고 보면 된다.

delete - 2 ) 형제가 black, 조카가 모두 black

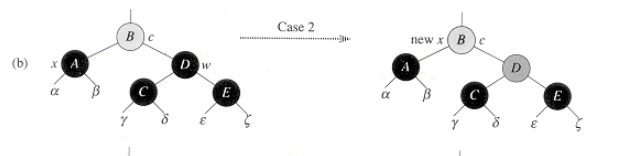
두번째 case이다.
부모의 색깔은 상관이 없고(red,black 모두 가능), 자신과 형제, 조카가 모두 black이다.

이 케이스는 오른쪽에 과다한 black이 발생 했을 때, 한쪽의 black 노드를 없애 균형을 맞추기 위해 사용한다.

보통 case1을 진행하고 난 후, C의 자식이 모두 black 일 경우에 발생하게 된다.

delete - 3 ) 형제가 black, 가까운 조카 red, 먼 조카 black

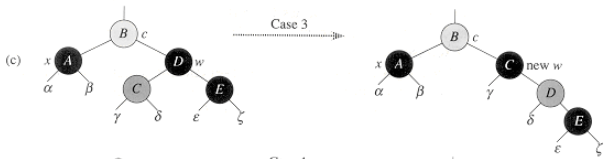
세번째 case다.
자신과 형제, 그리고 바깥쪽 조카는 black이고, 부모의 색깔은 상관없으며, 안쪽 조카는 red이다.

이 case도 case1과 같이 '전처리'과정이라고 보면 된다.
딱 위 그림의 왼쪽 모양은 정말 무슨 짓을 해도 균형을 맞출수 없는 '답없는'모양인데,
이럴때 '해결 가능한'모양으로 바꿔주기 위한 과정이라고 생각하면 된다.

그러니 case3를 실행하고 나면 case4를 하면 된다.

delete - 4 ) 형제가 black, 먼 조카 red

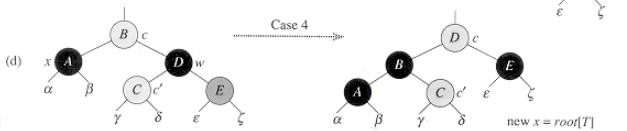
마지막이자, 네번째 case이다.

자신과 형제는 black이고, 부모와 안쪽 조카의 색깔은 상관 없으며, 바깥쪽 조카는 red이다.

이 그림은 case3 이후의 모습이다. 그래서 가만히 보고 있으면 왼쪽으로 black이 1 증가하는게 보일 것이다.
다르게 말하면 A노드는 변형 이전 B에서부터 1개의 black 을 거치면 도달할 수 있는데,
변형 후 에는 D에서부터 2개의 black을 거쳐야 도달 할 수 있게 되었다.

이렇게 되면 우리는 보통 의문을 가진다.
'아니 불균형이 생겨버리면 어쩌자는거임?'

하지만 하나 간과한 사실이 있다.
rb트리는 일부분의 문제를 해결하기 위한 여러개의 case를 통해 그래프를 fix하는 것이고
저 그래프는 다 그려진 것이 아니라는 것이다.

case3을 보자.
E 노드가 보이는가?

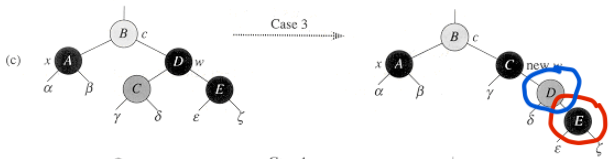
case3의 E노드는 case4의 E 노드 아래에 붙게 된다.

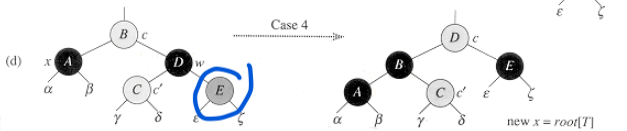
그렇다! 우리는 보이지 않는 black 노드가 숨어있다는 사실을 몰랐던 것이다!

그러니까 우리는 정체도 모르는 상상속의 트런들과 싸우고 있었던 것이다.

애초에 전체 트리의 일부분이라 완벽하지 않은, 트리의 '일부분'만 보고 생각하기 때문에 이게 어떻게 되는것일까 고민하게 되는것이다.
하지만 실제로는 우리의 예상과는 다르게 자기 혼자서 잘 작동하는 로직이었으며, 우리는 이게 어떻게 작동하는 것일까 걱정할 필요 없이 그냥 case 에서 시키는대로 똑같이 하면 된다.

고민하는 시간에 예제라도 한번 더 보고 시뮬레이션 사이트에서 노드 넣어보고 실험해보자!
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
(시뮬레이션 사이트)

진짜 rb트리를 c언어 처음 보는데 구현하라고 하니까 1주일간 죽을 맛이었다.
그나마 예시를 많이 접해보고 책도 이해가 되서 이해가 빨라 다행이긴 했지만
다른팀원들을 보니까 진짜 힘들어하시는 분도 많았다.

부디 이 글을 보는 다음 기수 분들은 고통받지 않았으면 한다.