프로그래머스 2021 국민대 여름방학 인공지능 과정 1주차 Day2 TIL

---

🔍Numpy란?

대규모 다차원 배열이나 벡터 등의 수치 연산을 쉽게 하도록 돕는 파이썬 라이브러리

---

📌선형대수 with Numpy

numpy에는 선형대수 관련 다양한 함수들이 있다.

import numpy as np

📄

• 영벡터 np.zeros(value or tuple) : 모두 0
• 일행렬 np.ones(value or tuple) : 모두 1
• 대각행렬 np.diag(main_diagonal) : main diagonal를 제외한 나머지 0
• 항등행렬 np.eye(n, (dtype)) : main diagonal이 1인 대각행렬
• 행렬곱 np.dot() or @ : 행렬 간 곱

📑

• 트레이스 np.trace() : main diaonal의 sum
• 역행렬 np.linalg.inv() : 행렬 A에 대해 AB = BA = I를 만족하는 행렬 B
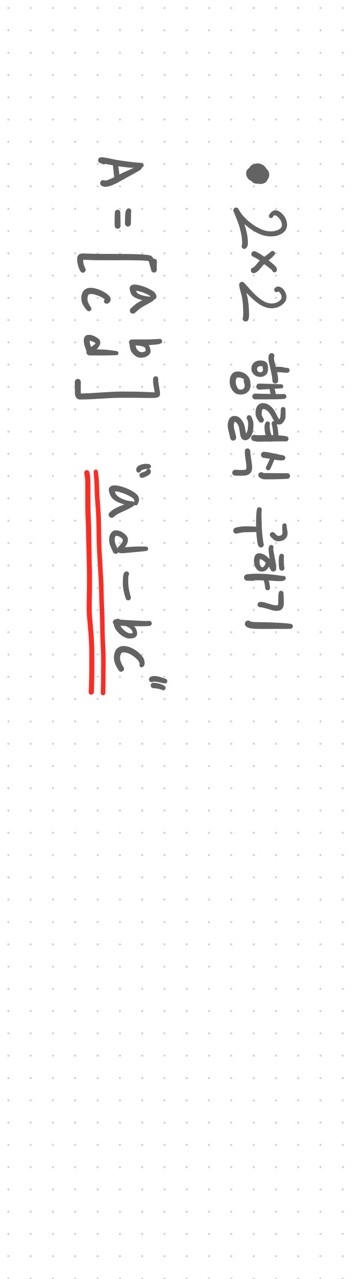
  검산은 mat @ np.linalg.inv(mat) == I
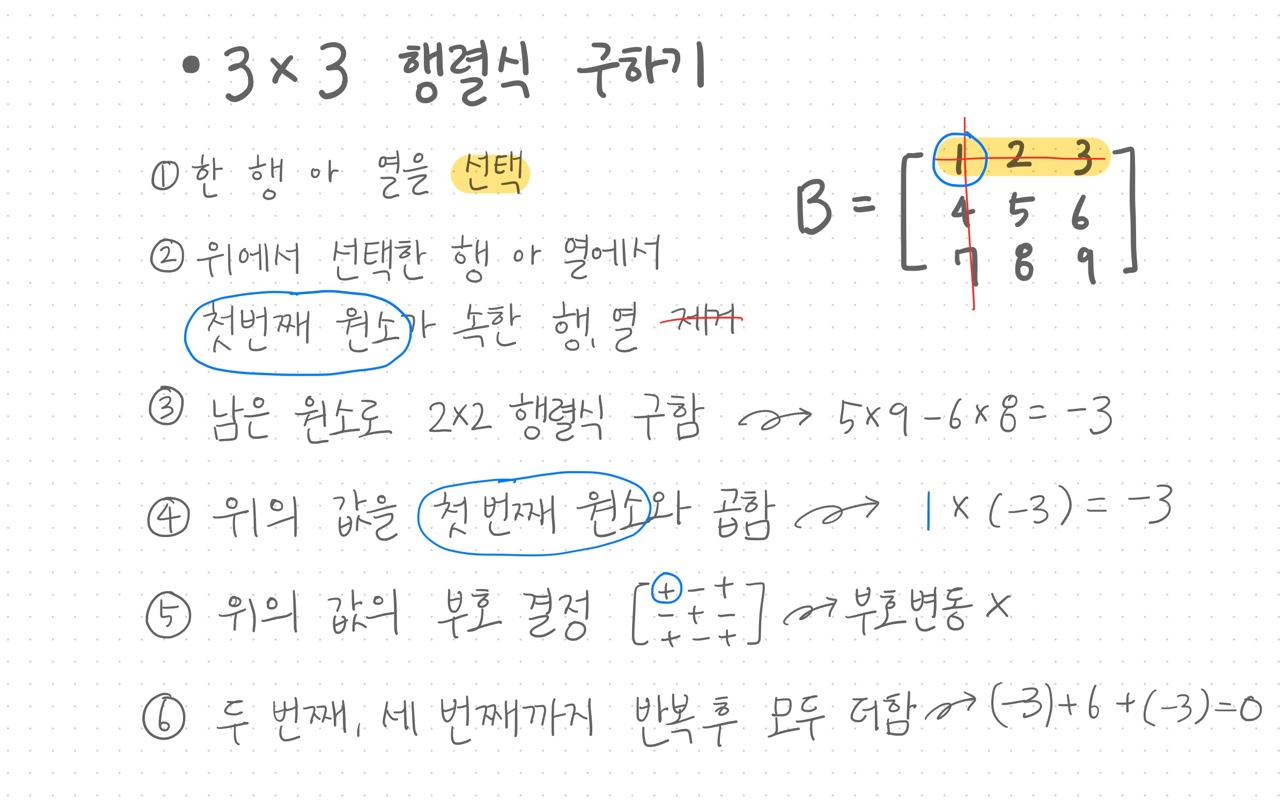
• 행렬식 np.linalg.det() : 행렬을 대표하는 값 중 하나

  arr = np.array([[1, 4, 7], [2, 5, 8], [3, 6, 9]])
  np.linalg.det(arr)
  
  >>0.0

• 고유값과 고유벡터 np.linalg.eig() : 정방행렬(nxn) A에 대해 $Ax = \lambda x$을 만족하는 고유값 $\lambda$ 와 고유벡터 x

  arr = np.array([[2, 0, -2], [1, 1, -2], [0, 0, 1]])
  np.linalg.eig(arr)
  >> (array([1., 2., 1.]),
      array([[0.        , 0.70710678, 0.89442719],
            [1.        , 0.70710678, 0.        ],
            [0.        , 0.        , 0.4472136 ]]))

  $Ax = \lambda x$ --> $(A-\lambda I)x = 0$ --> $det(A-\lambda I) = 0$

---

numpy 이름만 들어봤었는데 이런거였구나👀
선형대수를 까먹어서 정리를 좀 해야겠다 싶었다
근데 내가 행렬식이란 걸 배운적이 있었나 왜 기억이 안 나지ㅎㅎ😅