알고리즘

알고리즘

문제를 해결하기 위한 일련의 절차를 공식화한 형태로 표기한 것으로, 좋은 알고리즘을 만들기 위해서는 다음과 같은 조건을 충족해야한다.

1. 입력
   • 외부에서 제공되는 자료가 0개 이상 존재한다.
2. 출력
   • 적어도 2개 이상의 서로 다른 결과를 내어야 한다. 즉, 모든 입력에 하나의 출력이 나오면 안된다.
3. 명확성
   • 수행 과정은 명확하고 모호하지 않은 명령어로 구성되어야 한다.
4. 유한성
   • 유한 번의 명령어를 수행 후 유한 시간 내에 종료한다.
5. 효율성
   • 모든 과정은 명백하게 실행 가능(검증 가능)한 것이어야 한다.

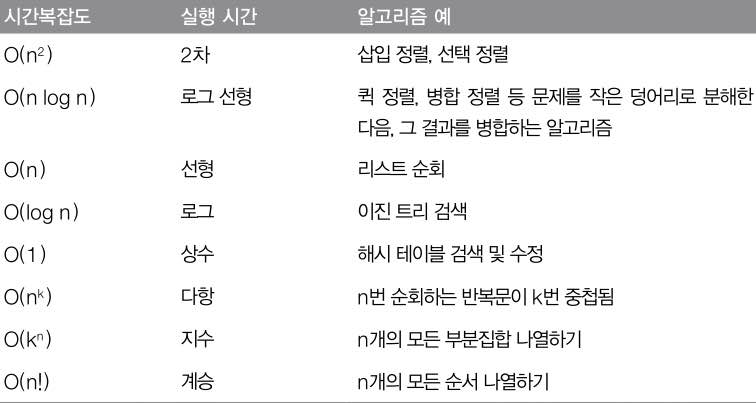
알고리즘에 필요한 개념으로는 시간 복잡도, 자료구조, 정렬이있다. 시간 복잡도는 문제를 해결하는데 걸리는 시간과 입력의 함수 관계이다.

알고리즘 종류

알고리즘의 종류로는 검색, 재귀, 정렬 알고리즘이 있다.

검색 알고리즘

1. 선형 검색 (Liner Search): 복잡도 O(n)
   • 배열을 검색하여 원하는 Key값을 찾는 알고리즘.
   • 배열의 맨앞부터 순차적으로 훑어가며 검색
2. 이진 검색 (Binary Search): 복잡도 O(log(n))
   • 정렬된 배열에서 원하는 key값을 찾는 알고리즘.
   • 선형검색보다 빠름

재귀 알고리즘

1. 파보나치 수열: 복잡도 O(2^n)
   • 파보나치 수열은 다음과 같이 무한대로 이어지는 수열이다.
   • 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ...
   • 처음 시작하는 두개의 값은 각각 0과 1로 주어진다.
   • 이후 스텝에서의 값은 앞 두개의 값을 더한것과 같다.
   • 재귀 호출 구조는 거듭되는 연산이 많아서 복잡하다.
2. 최대공약수(GCD): 복잡도 O(log(n+m))
   • 유클리드 알고리즘을 재귀호출 방법으로 사용할 수 있다.
   • a >= b라면 GCD(a,b) = GCD(b,r)이다. 여기서 r=a%b다. 즉, 나머지이다.
   • b가 0이 될때까지, 재귀호출을 반복한다. b가 0이되면, 최대공약수는 바로 a다.
3. 하노이의 탑알고리즘
   • 이미 알아본 방법으로 원반 n-1개를 옮긴다. (재귀호출)
   • 이미 알아본 방법으로 마지막 원반을 옮긴다. (재귀호출)

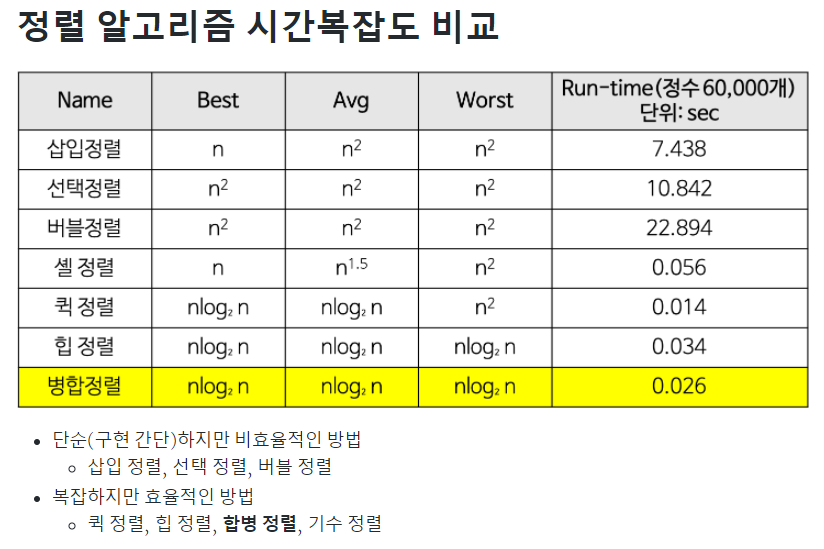
정렬 알고리즘

1. 선택정렬 (Selection Sort): 복잡도 O(n^2)
   • 리스트안에 있는 자료들 (소 -> 대) 순서로 나열하려고한다.
   • 가장 단순한 정렬이지만, 많이 비교하므로 복잡도가 높다.
   • 첫번째 값을 가져올 때 n-1회 비교하여 최솟값을 결과리스트에 가져온다.
   • 두번재 값을 가져올 때 n-2회 비교하여 최솟값을 결과리스트에 가져온다.
   • 반복한다. 즉, 전체 비교횟수는 n(n-1)/2다.
2. **삽입정렬 (Insertion Sort): 복잡도 O(n) ~ O(n^2)의 사이
   • 입력 리스트가 이미 정렬에 가까운 상태라면 복잡도는 낮아진다.
   • 일반적으로 선택정렬과 유사한 성능을 가진다.
   • 자료가 담긴 리스트에서 순차적으로 값을 가져온다. (첫째값을 그대로 가져옴.)
   • 두번째 값을 가져와서 결과리스트와 비교 후 위치를 정한다.
   • 반복한다.
3. **병합정렬 (Merge Sort): 복잡도 O(log(n))
   • 재귀호출을 사용하는 정렬
   • 분할정복 방법의 알고리즘이다.
   • 자료가 담긴 리스트를 가운데 기준으로 두개로 쪼갠다.
     - 각 리스트에 첫 값을 비교 후 작은 것을 골라 결과 리스트로 옮김
   • 이전스템 반복 (재귀호출)
4. Bubble Sort: 복잡도 O(n^2)
   • 리스트를 훑어가며 인접한 값 두개씩 비교해서 정렬
   • 더 이상 위치 변경이 필요가 없을 때가지 반복한다.