[LeetCode] 72. Edit Distance

이 문제는 편집 거리, Levenshetein 거리로 불리는 알고리즘을 알면 매우 쉬운 풀이가 가능하다.

1. word1의 길이를 m, word2의 길이를 n이라고 가정했을 때 (m+1) * (n+1)크기의 2차원 배열을 생성한다.

2. 배열의 첫번째 행과 열은 0부터 m, n까지 증가하는 수를 담는다.
   2-1. 이 때 증가하는 이유는 빈 문자열 "" 에서 해당 문자를 만들기 까지 필요한 연산의 수 이다.
   

3. 이제 채워지지 않은 요소부터 순회하며 이전 문자열을 만들기 까지의 최소 연산의 수 + 1로 값을 채우는데 공식은 다음과 같다.
   
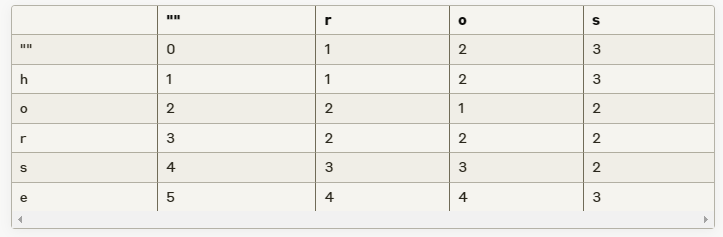
   3-1. 삭제 연산: dp[i - 1][j]
   3-2. 삽입 연산: dp[i][j - 1]
   3-3. 교체 연산: dp[i - 1][j - 1]

😎풀이

function minDistance(word1: string, word2: string): number {
    const m = word1.length
    const n = word2.length
    const dp = Array.from({ length: m+1 }, () => Array(n).fill(0))

    // 첫 행과 열 채우기
    for(let i = 0; i <= m; i++) dp[i][0] = i
    for(let j = 0; j <= n; j++) dp[0][j] = j

    for(let i = 1; i <= m; i++) {
        for(let j = 1; j <= n; j++) {
            if(word1[i - 1] === word2[j - 1]) {
                // 인덱스 값 일치 시 변경비용 X
                dp[i][j] = dp[i - 1][j - 1]
            } else {
                // 추가, 삭제, 변경 중 가장 효율적인 작업 실행
                dp[i][j] = Math.min(
                    dp[i - 1][j],
                    dp[i][j - 1],
                    dp[i - 1][j - 1]
                ) + 1
            }
        }
    }

    return dp[m][n]
};