[210419][백준/BOJ] 11726번 2×n 타일링

문제

입출력

풀이

2 x n 타일을 1 x 2, 2 x 1 타일로 채울 수 있는 방법의 개수를 구하는 문제이다.

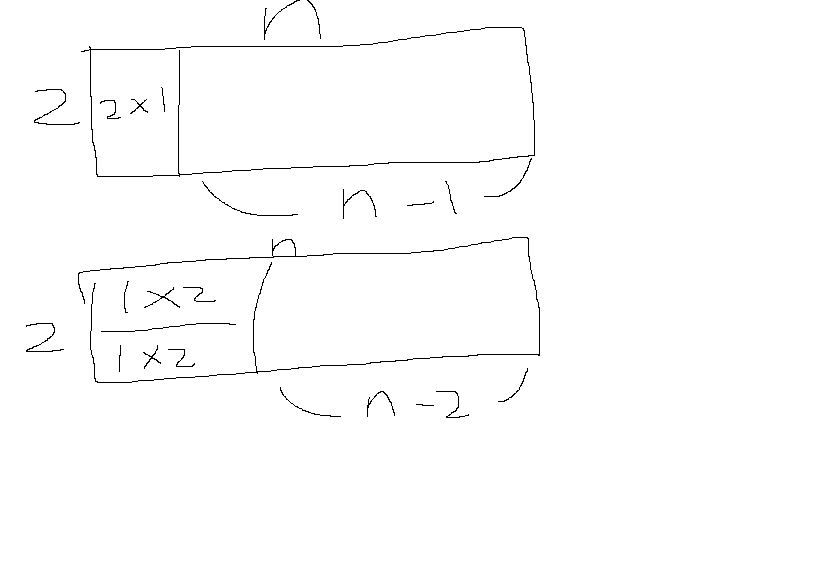
위 그림과 같이 2 x 1 타일로 채울 수 있는 방법의 수는 d[n-1], 1 x 2 타일로 채울 수 있는 방법의 수는 d[n-2]개 이므로 점화식은 d[n] = d[n-1] + d[n-2]이다.

또한 10007를 최종값에서 한번 나누면 시간초과가 발생하므로 계산할 때 마다 나누어줘야 한다.

코드

#include <bits/stdc++.h>
using namespace std;

int d[1002];

int dp(int n)
{
	d[1] = 1;
	d[2] = 2;

	for (int i = 3; i <= n; ++i)
		d[i] = (d[i - 1] + d[i - 2]) % 10007;
	return d[n];
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	int n;
	cin >> n;

	cout << dp(n);
}