[210124] 9번 모두의 약수(제한시간 1초)

KeonWoo Kim·2021년 1월 24일

목록 보기

2/84

문제

자연수 N이 입력되면 1부터 N까지의 각 숫자들의 약수의 개수를 출력하는 프로그램을 작성하
세요. 만약 N이 8이 입력된다면 1(1개), 2(2개), 3(2개), 4(3개), 5(2개), 6(4개), 7(2개), 8(4
개) 와 같이 각 숫자의 약수의 개수가 구해집니다.
출력은 다음과 같이 1부터 차례대로 약수의 개수만 출력하면 됩니다.
1 2 2 3 2 4 2 4 와 같이 출력한다.
출력 제한시간은 1초입니다.

▣ 입력설명
첫 번째 줄에 자연수 N(5<=N<=50,000)가 주어진다.
▣ 출력설명
첫 번째 줄에 1부터 N까지 약수의 개수를 순서대로 출력한다.

입출력

▣ 입력예제 1
8
▣ 입력예제 2
10000
▣ 입력예제 3
30000
▣ 입력예제 4
50000

▣ 출력예제 1
1 2 2 3 2 4 2 4

▣ 출력예제 2
1 2 2 3 2 4 2 4 3 4 2 6 2 4 4 5 2 6 2 6 4 4 2 8 3 4 4 6 2 8 2 6 4 4 4 9 2 4 4 8 2 8 2 6 6 4 2 10 3 6 4 6 2 8 4 8 4 4 2 12 2 4 6 7 4 8 2 6 4 8 2 12 2 4 6 6 4 ...
4 8 4 8 4 36 4 4 12 25

▣ 출력예제 3
1 2 2 3 2 4 2 4 3 4 2 6 2 4 4 5 2 6 2 6 4 4 2 8 3 4 4 6 2 8 2 6 4 4 4 9 2 4 4 8 2 8 2 6 6 4 2 10 3 6 4 6 2 8 4 8 4 4 2 12 2 4 6 7 4 8 2 6 4 8 2 12 2 4 6 6 4
...
8 16 4 8 8 6 16 8 4 50
▣ 출력예제 4
1 2 2 3 2 4 2 4 3 4 2 6 2 4 4 5 2 6 2 6 4 4 2 8 3 4 4 6 2 8 2 6 4 4 4 9 2 4 4 8 2 8 2 6 6 4 2 10 3 6 4 6 2 8 4 8 4 4 2 12 2 4 6 7 4 8 2 6 4 8 2 12 2 4 6 6 4
...
16 2 8 24 12 6 16 2 30

풀이

문제를 보자마자 일반적으로 약수의 갯수를 구하는 방법의 코드가 생각이 나서 약수를 구하기 위한 방식으로 문제를 풀었다.

코드

#include <iostream>
using namespace std;

int main()
{
	int n=0;

	cin >> n;

	for (int i = 1; i <= n; i++)
	{
		int cnt = 0;
		// 1 2 3 4 5 6 7 8
		for (int j = 1; j <= i; j++)
		{
			if (i % j == 0)
			{
				cnt++;
			}
		}
		cout << cnt << ' ';
	}
}

피드백

위의 방식은 10000까지는 정상적으로 출력이 된다. 그러나 30000과 50000은 제한시간 1초를 초과해서 시간초과가 발생하게 된다. 그 이유는 위의 코드의 시간 복잡도는 o(n^2)로 실행시간이 많이 걸리는 시간복잡도이기 때문이다.
따라서 다른 방법으로 문제를 해결해야 한다.

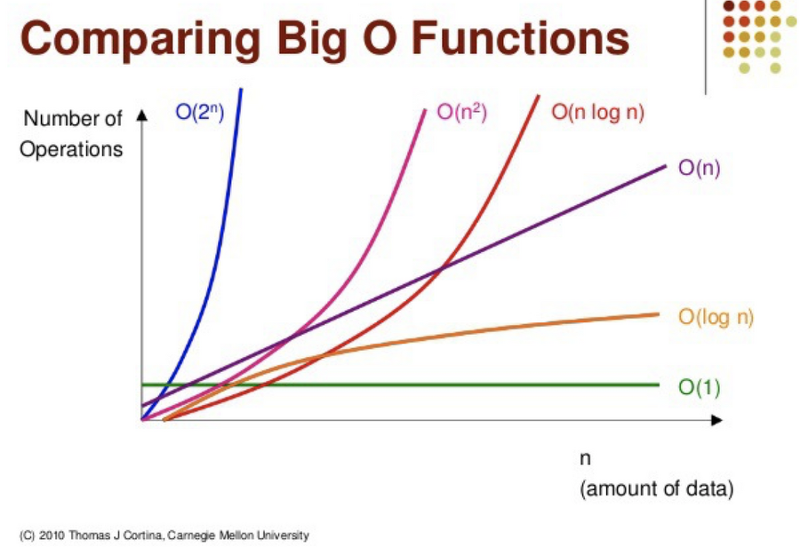
해결

8을 가지고 예시
전역변수로 0으로 초기화

i=1~n -> n회 반복
처음 반복문을 돌면서 i를 약수로 가지는 숫자들을 카운트하는 방식 -> i의 배수들

j=i~n j=j+i(i의 배수로 증가) -> n/i회 반복
i의 배수만큼 돌기때문에 계속 n번씩 도는 첫번째 코드보다 훨씬 효율적인 방법이다

1 2 3 4 5 6 7 8

cnt
1 1 1 1 1 1 1 1
1 2 1 2 1 2 1 2
1 2 2 2 1 3 1 2
1 2 2 3 1 3 1 3
1 2 2 3 2 3 1 3
1 2 2 3 2 4 1 3
1 2 2 3 2 4 2 3
1 2 2 3 2 4 2 4

i가 100일때 총 갯수가 50000이면 500바퀴만 돌면됨 -> 출력시간 감소
위의 방식은 시간복잡도가 nlogn보다는 실행시간이 느리지만 n^2보다는 실행시간이 빠른 방식이다.

또한 배열을 전역으로 선언하면 기본값이 0으로 초기화된다. 전역변수는 메모리 데이터 영역에 할당이 되며 크기가 큰 배열을 선언해도 문제없이 할당이 되지만 지역변수는 스택 영역에 할당이 되며 스택은 메모리가 작아 크기가 큰 배열을 선언하기에 적당하지 않다.

코드

#include <iostream>
using namespace std;

int cnt[50001];

int main()
{
	int n=0;

	cin >> n;
	
	for (int i = 1; i <= n; i++) 
	{
		for (int j = i; j <= n; j =j+i)
			cnt[j]++; //j가 i의 배수이므로 j를 ++
	}
	for (int i = 1; i <= n; i++)
		printf("%d ", cnt[i]);
}