알고리즘

A에서 C라는 점을 거쳐서 B로 갈 수 있을 때, A에서 C로 가는 거리가 A에서 B로 가는 거리보다 더 크므로 절대로 C를 통해 연결된 경로로 B에 최단 거리로 도달할 수 없다.A가 특정 노드가 아니라 최단 거리가 구해진 노드들의 집합으로 생각해보자. 매순간 집합들과

트리 형태의 자료 구조왼쪽 서브 트리와 오른쪽 서브 트리를 가짐루트 노드는 왼쪽 서브 트리의 모든 노드들보다 큼루트 노드는 오른쪽 서브 트리의 모든 노드들보다 작음거치는 노드들에 의해 특정 노드의 값의 범위가 정해질 수 있음전위 순회, 중위 순회, 후위 순회로 모든 노

힙트리의 성질을 이용해서 정렬시간복잡도는 O(NlogN)이며, 공간복잡도는 O(1)이다.부모 노드 1개와 자식 노드 2개의 구조를 이룬다.Stable하지 않은 정렬 알고리즘이다.루트 노드가 왼쪽 서브 트리의 노드들보다 크고 오른쪽 서브 트리의 노드들보다도 크도록 만들어

배열을 피벗을 기준으로 나눠서 정렬하는 방식피벗을 어떻게 선택함에 따라, 성능 차이가 존재최악의 경우 O(n^2)까지 발생할 수 있음베스트 케이스의 경우 O(nlogn)의 시간 복잡도를 가짐공간복잡도는 O(1)피벗을 선택하고, 피벗과의 값 비교를 통해서 왼쪽과 오른쪽

배열을 반으로 나눠서 재귀적으로 호출해서 정렬을 하는 방식리턴이 이루어질때, 정렬된 상태로 리턴시간복잡도는 O(NlogN), 공간복잡도는 O(N)이다.함수를 호출하는 공간복잡도는 O(logN)이지만, 배열을 선언하는 공간복잡도가 O(N)이므로 O(N)안정 정렬재귀적으로

나도 처음엔 같은줄 알고, 무분별하게 사용했었다. 하지만, 그걸 깨준 문제가 있어서 공유하려고 한다.https://www.acmicpc.net/problem/15681위 문제를 풀어보면, Split으로 풀어보면 무조건 틀린다. 무슨 입출력으로 장난을 치냐 생각

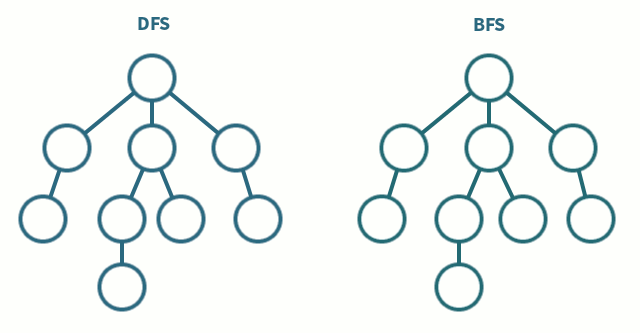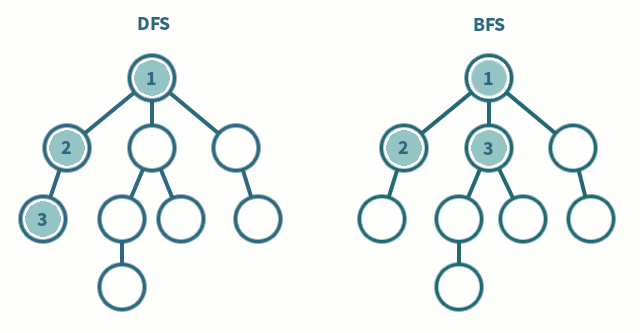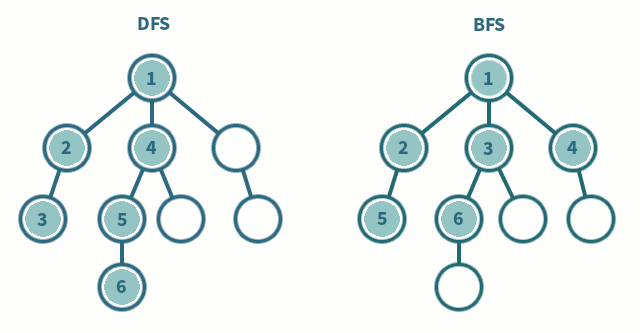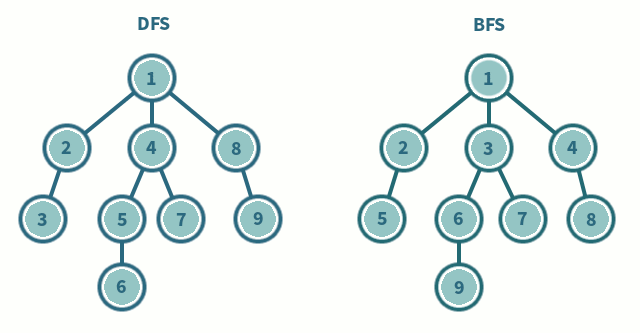
깊이 우선 탐색호출되는 함수의 구조를 트리로 보면, 매 호출마다 트리의 높이가 증가BFS와 다르게 리턴 동작이 존재(이전 높이로 돌아온다)시간복잡도는 O(V + E), 모든 V를 방문해서 총 E번만큼 움직이므로너비 우선 탐색호출되는 함수의 구조가 트리라면, 같은 높이의

해쉬 자료구조의 Key는 중복이 없음HashSet은 Key만 존재 HashMap은 Key와 Value가 존재Hash 자료구조에 사용되는 Key는 해쉬 관련 함수를 오버라이딩 해야함eKey값이므로, 고유한 값Key가 동일하면, 이전 객체가 덮어씌워짐equals에 의해서

출발지로부터 다른 목적지들로 최단 거리를 구할 수 있음다익스트라와 다르게 음수 사이클에 대해서 확인 가능시간복잡도는 O(V \* E)거리 배열을 출발지만 0으로 만들어놓고 나머지는 모두 최댓값으로 갱신매 단계에서 모든 간선을 검사하므로, 출발지부터 점차 확장되면서 거리