[딥러닝]합성곱 신경망

5.1 합성곱 신경망

합성곱 신경망
이미지 전체를 한 번에 계산하는 것이 아닌 이미지의 국소적 부분을 계산함으로써 시간과 자원을 절약하여 이미지의 세밀한 부분까지 분석가능한 신경망

5.1.1 합성곱층의 필요성

합성곱 신경망은 이미지, 영상 처리에 유용

• 이미지 분석의 과정
  배열을 펼친 다음, 픽셀에 가중치를 곱해 은닉층으로 전달 (다차원 → 1차원)
  펼처서 분석하면 데이터의 공간적 구조를 무시하게 되는데, 이를 방지하기 위한 것이 합성곱층

###5.1.2 합성곱 신경망 구조

• 합성곱 신경망 (CNN)
  음성 인식이나 이미지/ 영상 인식에서 주로 사용되는 신경망
  다차원 배열 데이터를 처리하도록 구성되어 컬러 이미지 같은 다차원 배열 처리에 특화

• 합성곱 층의 구성
  입력층
  합성곱층
  풀링층
  완전연결층
  출력층

• 과정
  합성곱 신경망은 합성곱층과 풀링층을 거치며 입력 이미지의 주요 특성 벡터 추출
  추출된 주요 특성 벡터들은 완전연결층을 거치면서 1차원 벡터로 변환
  출력층에서 활성화 함수인 소프트맥스 함수를 사용해 최종 결과 출력

• 입력층 (input layer)
  입력 이미지 데이터가 최초로 거치는 계층
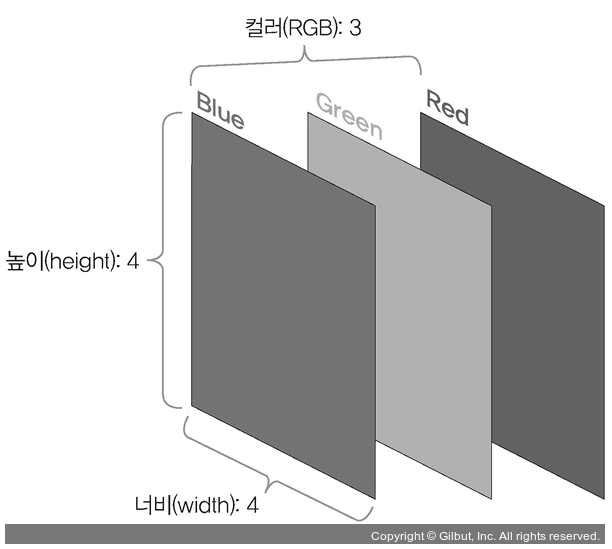
  이미지는 단순 1차원 데이터가 아닌, (높이, 너비, 채널)의 3차원 데이터
  이때 채널은 이미지가 그레이스케일 → 1, 컬러 → 3 (RGB)

• 합성곱층 (convolutional layer)
  입력 데이터에서 특성을 추출하는 역할
  특성을 감지하기 위해 커널이나 필터 사용
  커널/필터는 이미지의 모든 영역을 훑으면서 특성 추출 → 특성 맵(feature map)

• 스트라이드가 1일 때 이동하는 과정

스트라이드(stride) : 필터를 적용하는 위치의 간격
스트라이드가 2이면 필터를 적용하는 윈도우가 2칸씩 이동

1단계 : 입력 이미지에 3x3 필터 적용
입력 이미지와 필터를 포개 놓고 대응되는 숫자끼리 곱한 후 더함

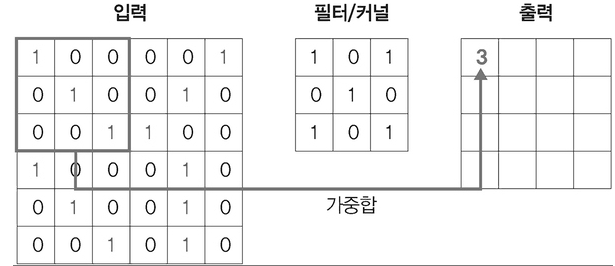
2단계 : 필터 1만큼 이동 후 같은 방식으로 연산

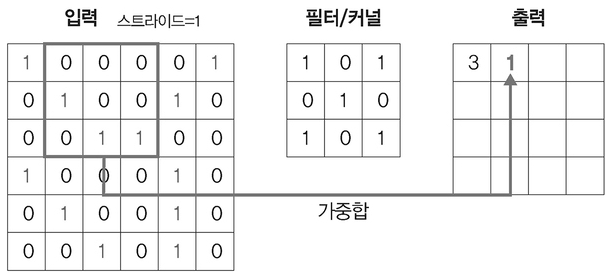
이후 단계 : 마지막 필터까지 이동

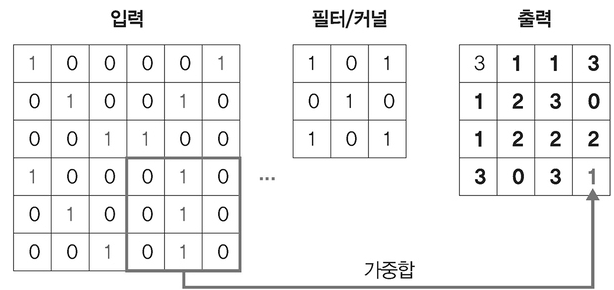
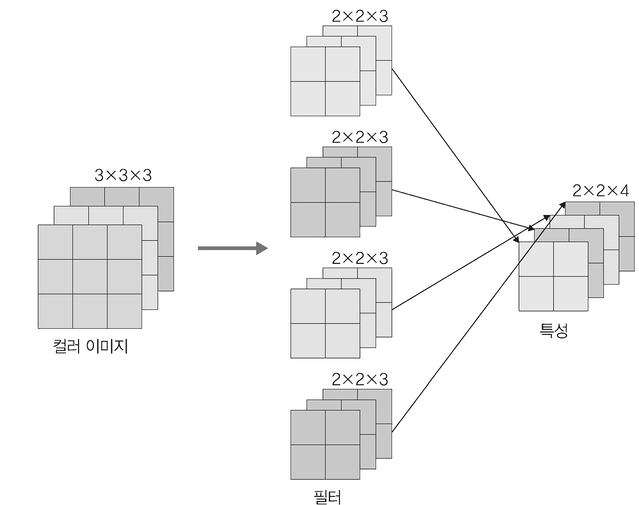
• 컬러에서의 계산
  필터 채널이 3이라는 것과 둘째, RGB 각각에 서로 다른 가중치로 합성곱을 적용한 후 결과를 더해줌 (단, 채널이 3개여도 실제 필터 개수는 1개, 1개씩 총 3개인거임!!)

필터가 2개 이상인 합성곱은?
필터가 두 개 이상이면 필터 각각은 특성 추출 결과의 채널

• 풀링층 (pooling layer)
  특성 맵의 차원을 다운 샘플링하여 연산량을 감소시키고, 주요한 특성 벡터를 추출하여 학습을 효과적으로 할 수 있게끔 함. (픽셀 감소라고 생각하면 이해하기 편합니다.)

• 풀링 연산의 기법
  최대 풀링 (max pooling) : 대상 영역에서 최댓값 추출
  평균 풀링 (average pooling) : 대상 영역에서 평균을 반환
  → 대부분은 최대 풀링 사용

• 최대 풀링 계산
  주어진 스트라이드를 기준으로, 최댓값 선택

• 평균 풀링 계산
  

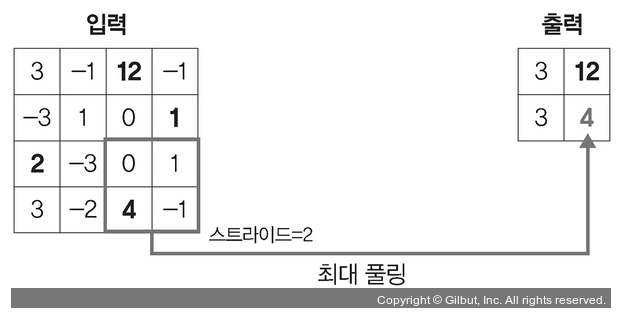
0=(3+(-1)+(-3)+1)/4

3=(12+(-1)+0+1)/4

0=(2+(-3)+3+(-2))/4

1=(0+1+4+(-1))/4

• (fully connected layer)
  이미지는 3차원 벡터에서 1차원 벡터로 펼쳐지게 됨 (flatten)

• 출력층
  소프트맥스 활성화 함수가 사용
  입력받은 값을 0~1 사이의 값으로 출력
  이미지가 각 레이블에 속할 확률 값 출력, 가장 높은 확률 값을 갖는 레이블이 최종 값으로 선정

5.1.3 1D, 2D, 3D 합성곱

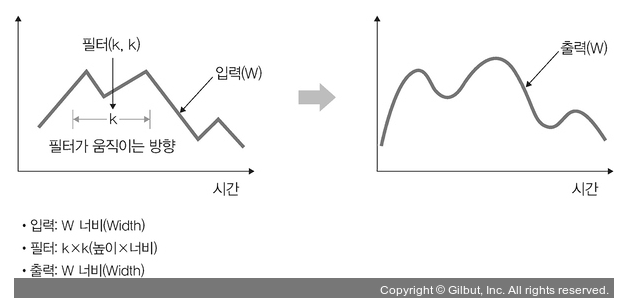
• 1D 합성곱
  필터가 시간을 축으로 좌우로만 이동할 수 있는 합성곱
  입력(W)과 필터(k)에 대한 출력은 W가 됨.
  그래프 곡선을 완화할 때 많이 사용
  자연어 처리에서 주로 많이 사용함
  

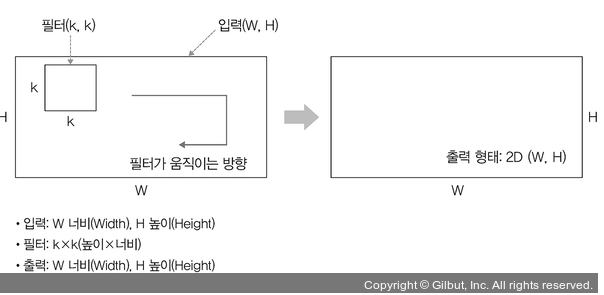
• 2D 합성곱
  방향 두 개로 움직이는 형태
  입력(W, H)과 필터(k, k)에 대한 출력은 (W, H)가 되며, 출력 형태는 2D 행렬
  

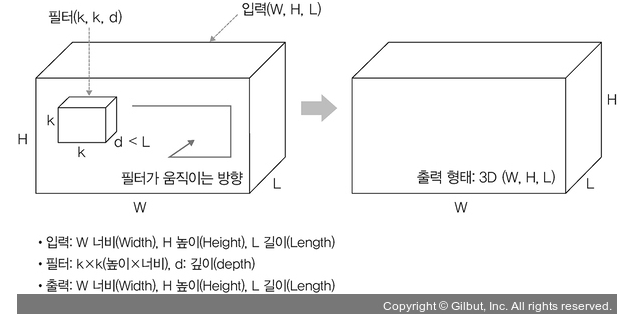
• 3D 합성곱
  입력(W, H, L)에 대해 필터(k, k, d)를 적용하면 출력으로 (W, H, L)을 갖는 형태
  출력은 3D 형태이며, 이때 d < L을 유지하는 것이 중요
  

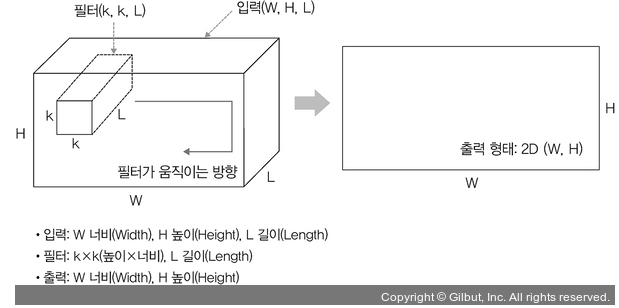
• 3D 입력을 갖는 2D 합성곱
  3D 형태임에도 출력 형태가 3D가 아닌 2D 행렬을 취하는 것
  필터에 대한 길이(L)가 입력 채널의 길이와 같아야 하기 때문
  입력(W, H, L)에 필터(k, k, L)를 적용하면 출력은 (W, H)
  ex) LeNet-5, VGG
  

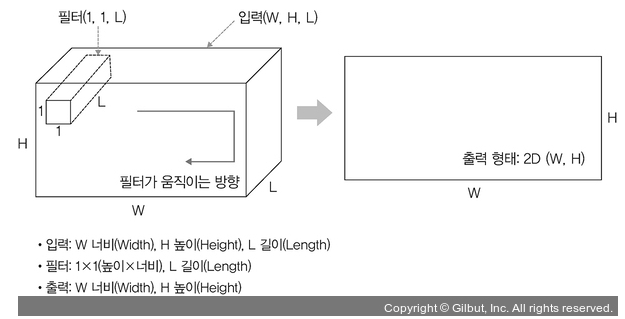
• 1x1 합성곱
  3D 형태로 입력
  입력(W, H, L)에 필터(1, 1, L)를 적용하면 출력은 (W, H)
  채널 수를 조정해 연산량이 감소되는 효과, ex)GoogleNet
  

5.3 전이 학습

큰 데이터셋을 필요로 하는 문제점을 보완하기 위한 현실적인 해결책이 전이 학습
아주 큰 데이터셋을 써서 훈련된 모델의 가중치를 가져와 해결하려는 과제에 맞게 보정해서 사용하는 것
아주 큰 데이터셋을 사용하여 훈련된 모델을 사전 훈련된 모델(네트워크)라고 함
→ 비교적 적은 수의 데이터를 가지고도 원하는 과제 해결 가능

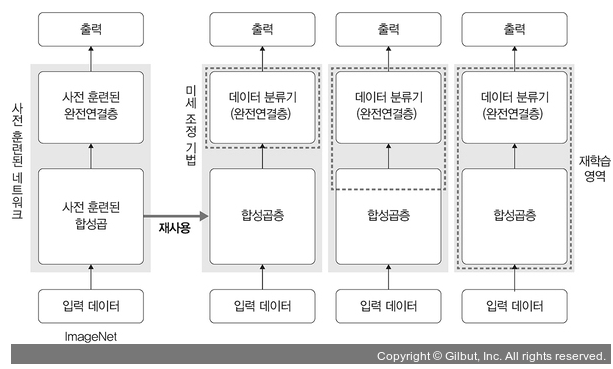
5.3.1 특성 추출 기법

• 특성 추출 (feature extraction)
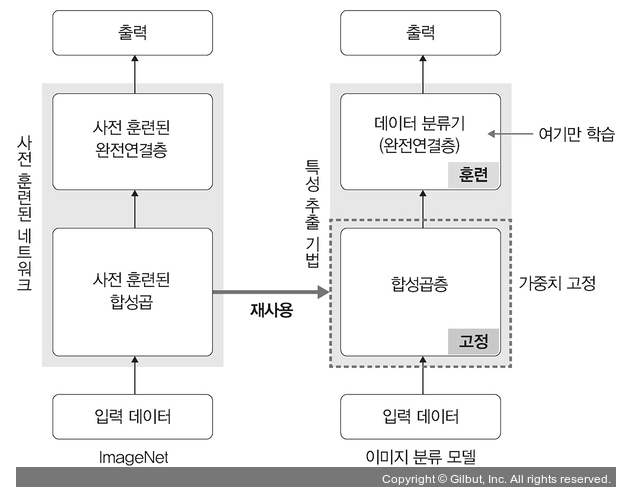
  ImageNet 데이터셋으로 사전 훈련된 모델을 가져온 후 마지막에 완전연결층 부분만 새로 만듦
  즉, 학습할 때는 마지막 완전연결층(이미지의 카테고리 결정 부분)만 학습, 나머지 계층은 학습 x

• 특성 추출의 분류
  • 합성곱층 : 합성곱층, 풀링층으로 구성
  • 데이터 분류기 (완전연결층) : 추출된 특성을 입력받아 최종적으로 이미지에 대한 클래스를 분류하는 부분

**사전 훈련된 네트워크의 합성곱층(가중치 고정)에 새로운 데이터를 통과시키고, 그 출력을 데이터 분류기에서 훈련

ex)Xception, Inception V3, ResNet50, VGG16, VGG19, MobileNet**

5.3.2 미세 조정 기법

• 미세 조정 기법

  • 특성 추출 기법에서 더 나아가 사전 훈련된 모델과 합성곱층, 데이터 분류기의 가중치를 업데이트하여 훈련시키는 방식

  • 특성 추출이 잘못되었을 때 미세 조정 기법을 이용하여 새로운 이미지 데이터를 사용하여 네트워크의 가중치를 업데이트해서 특성을 다시 추출할 수 있음.
    → 사전 학습된 모델을 목적에 맞게 재학습시키거나 학습된 가중치의 일부를 재학습시키는 것

  • 사전 훈련된 네트워크를 미세 조정하여 분석하려는 데이터 셋에 잘 맞도록 모델의 파라미터를 조정하는 기법

• 데이터셋이 크고 사전 훈련된 모델과 유사성이 작을 경우 : 모델 전체 재학습

• 데이터셋이 크고 사전 훈련된 모델과 유사성이 클 경우 : 합성곱층의 뒷부분(완전연결층과 가까운 부분)과 데이터 분류기 학습

• 데이터셋이 작고 사전 훈련된 모델과 유사성이 작을 경우 : 합성곱층의 일부분과 데이터 분류기 학습 → 데이터가 적어서 일부 계층에 미세 조정 기법 적용해도 효과가 없을 수 있기에 어디까지 새로 학습시켜야 할지 적당히 설정해주어야 함.

• 데이터셋이 작고 사전 훈련된 모델과 유사성이 클 경우 : 데이터 분류기만 학습. 많은 계층에 미세 조정 기법을 적용하면 오히려 과적합 발생 가능성 존재
  

5.4 설명 가능한 CNN

• 설명 가능한 CNN
  딥러닝 처리 결과를 사람이 이해할 수 있는 방식으로 제시하는 기술

CNN을 구성하는 각 중간 계층부터 최종 분류까지 입력된 이미지에서 특성이 어떻게 추출되고 학습하는지를 시각적으로 설명할 수 있어야 결과에 대한 신뢰성을 얻을 수 있음

5.4.1 특성 맵 시각화

• 특성 맵 (feature map)
  입력 이미지 또는 다른 특성 맵처럼 필터를 입력에 적용한 결과

출력층에 가까워질수록 원래 형태는 찾아볼 수 없음, 이미지 특징들만 전달되는 것 확인

5.5 그래프 합성곱 네트워크

• 그래프 합성곱 네트워크
  그래프 데이터를 위한 신경망

5.5.1 그래프란

• 그래프
  • 방향성이 있거나 없는 에지로 연결된 노드의 집합
  • 노드, 에지 : 일반적으로 풀고자 하는 문제에 대한 전문가 지식이나 직관 등으로 구성
  • 노드 : 원
  • 에지 : 두 노드를 연결한 선

5.5.2 그래프 신경망

• 그래프 신경망 (GNN)
  그래프 구조에서 사용하는 신경망

• 그래프 신경망의 과정

  • 1단계 : 인접 행렬
    네트워크 존재 시 노드 n개를 nxn 행렬로 표현
    인접 행렬 내의 값은 Aij는 i와 j의 관련성 여부’를 만족하는 값으로 채워짐
    → 인접 행렬 과정은 컴퓨터가 이해하기 쉽게 그래프로 표현하는 과정

  • 2단계 : 특성 행렬
    인접 행렬만으로 특성을 파악하기 어렵기에 단위 행렬 적용
    각 입력 데이터에서 이용할 특성 선택
    특성 행렬에서 각 행은 선택된 특성에 대해 각 노드가 갖는 값을 의미

→ 특성 행렬 과정을 거쳐 그래프 특성 추출

5.5.3 그래프 합성곱 네트워크

• 그래프 합성곱 네트워크
  이미지에 대한 합성곱을 그래프 데이터로 확장한 알고리즘

• 그래프 합성곱 네트워크 구조

  • 리드 아웃
    특성 행렬을 하나의 벡터로 변환하는 함수
    전체 노드의 특성 벡터에 대해 평균을 구하고 그래프 전체를 표현하는 하나의 벡터 생성