251018
시간복잡도_정말 중요
-
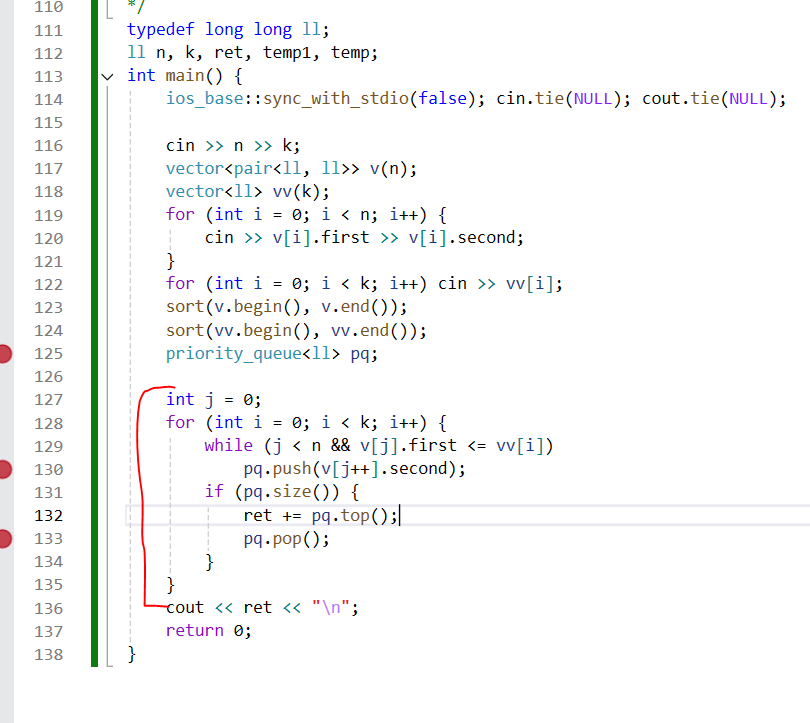
어쨋든 가방 k 번은 for문 돌려야 하므로 30만이다.
-
할 수 있는거는 보석의 시간복잡도를 줄여야 하는데
보석 n 도 30만이다. -
가방의 가장 작은 무게를 타겟으로 해서 보석도 가장 작은 무게로 진행하면서 동일할때까지 pq에 넣고,
-> for문 마지막에 가방에 하나 넣는 식으로 생각했다.
=> 그런데 이렇게 하게 되면 k * nlogn 의 시간복잡도가 아닐까?
라는 생각을 함.

-
하지만 그렇지 않다..
-> 코드를 잘 보면 매 k번 돌때마다 반드시 0~n번 만큼의 순회가 일어나는 것은 아니다.
--> j값이 진행할때마다 j값은 0부터 시작하는 것이 아니므로
이 때의 시간 복잡도는 k + nlogn 라고 할 수 있다.
-
참고 사이트
https://www.acmicpc.net/board/view/146580
250706
틀림.
알고리즘 유형
- pq.top()을 높게 만들기
: 하나의 가방 확정되는 순간에 pq.top을 pop 한번만 하고,
pq 를 그대로 가지고 가는 문제 .
- 1781 컵라면과는 다른 문제이고, 유형 분석 확실히 하자.
문제 해결 전략
-
완탐으로 하기에는 n과 k의 시간복잡도가 30만이다.
가방에다 어떤 보석을 넣을지 경우의 수 정하는 것은
시간복잡도가 매우 크므로 완탐은 불가 -
힌트
: 최대값을 구하는 문제이고, 간격을 가지고 있다.
-> 그리디를 생각 할 수 있고, -
보석과 가방을 오름차순으로 정렬해서
가장 효율이 높은 것을 pq에 넣어서 접근해야겠다 판단함. -
그리고 일단 2중 for문은 안된다.
: 30만 * 30만이다.
반례를 통해 생각해보기
// day,pay
// 1,65 1,70 2,99 2,88 3,50 5,500
// 가방의 무게
// 1 10
- -> 이런상황에서는 2,99 와 5,500을 선택하는 것이 최선이다.
// 1,65 1,70 2,19 2,8 3,15 5,5
// 가방의 무게
// 1 10
- -> 이런 상황에서는 1,65 / 1,70 인데 이거를 어떻게 코드로 표현할 수 있을까?? 에 대해서 고민을 했고,
결국 해결하지 못함.
문제 접근.
- 가방의 개수만큼만 보석을 담을 수 있다.
즉 가방의 개수라는 고정값이 있다.
-> 첫번째로 가방의 개수만큼 for문을 돌리자.
그러면서 아래에 target 을 가방 원소로 하고
1,65 넣었고 -> pq.size() = 1
그 뒤로 1,70 을 비교해서 하기에는
최대값이 뒤에 있는 것을 넣기보다는 아깝다.
pq에서 바로 빼지 말고, 뭔가를 해야 겠다. 는
생각이 든다....
- 여기서 1,65를 빼면 최대값 안된다.
// 1,65 1,70 2,19 2,8 3,15 5,5
// 가방의 무게
// 1 10
// -> 135
-
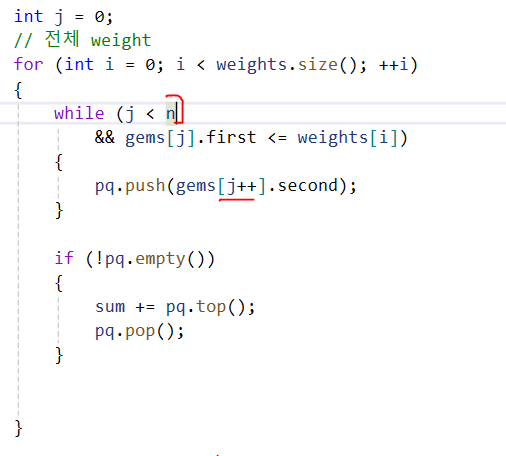
1) 이렇게 생각해보자.
: pq의 top에는 높은값이 오게 하자. -
2) 그리고 가방의 무게 보다 작은 weight 보석을 전부다 pq에 넣는다.
그리고 weight가 가방보다 높으면 중지, -
3) 타겟 가방에다가 보석을 넣어야 한다.
가장 높은거 꺼내서 가방에다가 넣어놓는다. -
4) pq에 넣은 상태로 for문 다시 돌아와서 다음 가방 무게를 가지고 증가된 보석의 인덱스를 가지고 pq에다가 삽입
-
5) 2번과 3번을 반복하게 되면서 종료.
시뮬레이션
// 1,65 1,70 2,19 2,8 3,15 5,5 ,
// 가방의 무게
// 1 10
// -> 135
- 위의 거를 가지고 해보자.
가)
무게가 1인 가방을 타겟으로 하고 현재 pq는 empty이다.
무게가 1인 보석은 2개가 있고, pq에 넣자.
pq : 70 65가 담기고
무게가 2인 보석이기 때문에 pq push 끝
무게가 1인 가방에다가 보석 70을 넣자.
나)
무게가 10인 가방을 타겟으로 하고 현재 pq에는 65이 있다.
무게가 2 , 2 ,3 ,5를 넣자.
pq : 65 , 19 ,15, 8,5
보석 없으니 pq에 push 끝
마지막에 무게가 10인 가방에 가치가 가장큰 top인 보석을 넣자.
-> 65를 넣자.
코드