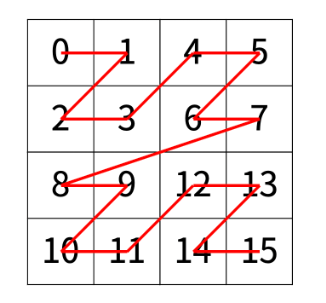
첫번째 풀이

: 너무 어렵게 생각했다.

• 접근 방법은 맞았다!

• 좀 더 쉽게 접근할 수 있는 방법이 없을까???? 생각해보자..

int n, r, c;
// 너무 어렵게 생각했다.... 
int quadTree(int _sX , int _sY, 
		int _eX, int _eY, int _size)
{
	int halfSize = _size / 2;

	if (_sX <= c && c <= _eX
		&& _sY <= r && r <= _eY)
	{
		//return quadTree();
	}
	else
		return _size;

	int res = 0;
	// 00 44 8 

	// 00 22 
	res += quadTree(_sX, _sY, _sX + halfSize, 
		_sY + halfSize, halfSize);
	// 20 42
	res += quadTree(_sX + halfSize, _sY, _eX ,
		_sY + halfSize, halfSize);
	// 02 24 행렬 로는 0~2 / 2 ~4 인데 rc를 반대로 해야 겟다. 
	res += quadTree(_sX , _sY + halfSize, _sX + halfSize,
		_eY, halfSize);
	// 22 44
	res += quadTree(_sX + halfSize, _sY + halfSize,
		_eX, _eY, halfSize);

}

int main()
{
	// n은 15이고 
	// 15 * 15 
	// r이나 c는 2의 15승이다. 
	//2dml 10승은 3만 2천이다. 

	// 160000 0000

	// 완탐으로 하기에는 시간초과된다. 


	// 문제를 보고 쿼드 트리가 생각난다... 

	// 2 3 1 의 경우 
	// 4 * 4이고 
	// 4분할로 분리하면 
	// 00 ~ 11 size : 4 / 2  -  02 ~ 13 / 20 ~ 31
	// 이런식으로 분리되고, 
	// 3행 1열은 20~31에 있으니까. 여기로 또 진입한다.
	// 이런식으로 재귀를 통해서 진입하다 보면 찾을수 있다? 
	// 몇번째 인지를 알아야 한다. 

	// 그러면 만약에 4덩어리라고 한다면
	// 3번째 진입이고 
	// 1,2번 사각형은 8번 진입이 완료된 상태이다.
	// 그럼 3번째 사각형에서의 31번호만 찾으면 된다. 

	
	cin >> n >> r >> c;


	int ssize = pow(2, n);
	
	quadTree(0, 0, ssize , ssize , ssize);

}

2번째 풀이

: 불필요한 4사분면 사각형의 크기까지 누적된다...

3번째 풀이

: 불필요한 범위에 있는 친구는 누적되지 않게 void 형으로 변경하고,
불필요한 범위에 도달하기 전에 r,c 찾으면 출력하고 뛰쳐나오자.

• 중요한 부분은 범위값이다.
  시작 인덱스의 경우는 -1 할 필요가 없다. 범위가 아니라 해당 범위를 포함한 상태에서 시작하여야 하기 때문이다.

• 범위 체크를 변경했는데 왜냐하면 지금의 경우는 00 ~ 11 까지 이고,
  01 ~~ 13 까지이다. size는 마지막 인덱스에 포함되면 안된다!

https://www.acmicpc.net/submit/1074/86070626