도출
문제에서 원하는 것은 좌측상단에 위치한 동전을 최대 몇번 움직이는지이다.
: 타겟팅은 memo[0][0]으로 접근해야 함.
-
다음 값에다가 누적하는 것이 아니라, 시작되는 원소의 인덱스에다가 누적시키는 것임..
memo[0][0]에서 동전 보낼 수 있는 최대한의 횟수는?
그래야 백트래킹을 돌면서 0,0의 dp에 누적을 한다던지, 최대값 계산을
처리하는 방식으로 함. -
왜 dp 값 유무에 따라서 반환처리 하는 것일까?
1) 우회하면서 들어오면 갱신되지 않을까?에 대한 부분이다.
but 0,0을 기준으로 갱신을 하게 되고, 최대값을 갱신하는 것이니
내가 하는 생각은 하지 않아도 됨.
-> 연결되어 있는 함수로 계속 넘어가므로 이러한 생각은 안해도 됨.
기준은 0,0 에서 max로 확인하게 되므로

기준을 nestIndex가 아니라 0,0으로 놓고 생각하면 이러한 고민할 필요가 없음.
핵심
2) 시간 초과 하게 됨. 왜냐하면, 방문을 해서 기록을 했는데도 계속해서 탐색을 하게 되므로 문제임. 최대값 갱신은 다른 곳에서 하고 있기 때문에,
이미 dp에 있다면 , 더 탐색할 필요 없이 기존 값을 반환하도록 하자.
https://www.acmicpc.net/board/view/82361
😨코드는 외워버릴 수 있지만, 놓칠 수 있는 부분
-
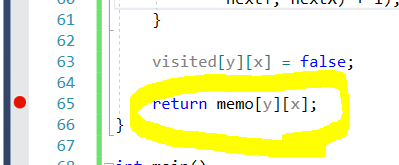
반환을 어떻게 처리할 것인가?
1) 반환되고 끝부분에서 memo 처리된 부분들을 이전 원소에 카운팅을 해야함.

-
백트래킹이 완료된 후, 누적되는 값을 이전원소와 비교할 수 있도록,
반드시 반환을 해야함.
도전 횟수
- 220902
- 220901
- 220831
주의할점.
1) 인접한 부분을 반복문에서 체킹하는 continue 부분을 하면 안됨.
: 여기서 체킹을 해버리면 , 9에서 continue되어버리는데,
내가 만든 의도대로 프로세스가 동작되게 하려면, continue가 되면 안되고,
return 0이 나오게 해야 함.
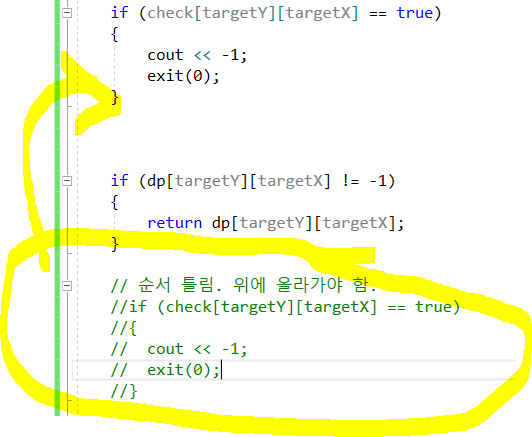
2) 반환되는 순서도 중요함.
- 이유? : 최우선으로 왔다리깟다리 체크를 해야하니까.
왔다리갔다리를 먼저 체킹을 해야함.
그 이후에 dp값 최대값 유무를 확인을 해야함.
3) memset
-> cstring 헤더를 추가해야 함.
최종 코드
#include <iostream>
#include <vector>
#include <cstring>
#include <string>
#include <algorithm>
using namespace std;
// 1103번. 게임
// 16: 27~ 16:58 1단계
// 수정 들어감. ~ 17:22
// bfs 아님.
// 백트래킹으로 풀어야 겠음.
// 시간복잡도 50 * 50 * 4
// 예제 입력1번으로 반례에 대해
// 생각을 해보면,
// 내가 상상한 프로세스 돌고 돌리면서 계속 나아가다가
// 이미 방문한 곳에 다시 들어갈 경우도 계속 카운팅을 진행하려고 함.
// 이렇게 되면 최악의 경우, 시간 초과됨.
// => 메모이제이션을 사용해야 겠음.
// 기준으로 변경함!
// 타겟이 되는 인덱스를 기준으로 해서
// 최대값이 설정된 인덱스는 그냥 반환하자.
// 재귀들어가지 말고, 어차피 몇번 진행되었는지 최대값은
// 기록되었기 때문임.
// 상하좌우
int dy[]{ -1,1,0,0 };
int dx[]{ 0,0,-1,1 };
int dp[51][51];
int n, m;
int dfs(vector<vector<char>>&v , vector<vector<bool>>&check
, int targetY, int targetX)
{
if (targetY < 0 || targetY >= n
|| targetX < 0 || targetX >= m)
{
return 0;
}
if (v[targetY][targetX] == 'H')
{
return 0;
}
if (check[targetY][targetX] == true)
{
cout << -1;
exit(0);
}
if (dp[targetY][targetX] != -1)
{
return dp[targetY][targetX];
}
// 순서 틀림. 위에 올라가야 함.
//if (check[targetY][targetX] == true)
//{
// cout << -1;
// exit(0);
//}
int value = v[targetY][targetX] - '0';
// 왔다리 갔다리의 경우를 처리해야 함.
check[targetY][targetX] = true;
for (int i = 0; i < 4; ++i)
{
int nextY = targetY + dy[i] * value;
int nextX = targetX + dx[i] * value;
// 테두리 확인 -> 테두리 확인도 잘못됨.
//if (nextY < 0 || nextY >= n
// || nextX < 0 || nextX >= m)
//{
// continue;
//}
//안으로 들어가야 하는데..
// 메모이 제이션으로 기록을 해야 함.
// 기록되어 있을 경우에는 리턴시키자.
//현재값을 기준으로 해서 몇번의 최대값이 갱신되는지를
// 작성해야 함.
dp[targetY][targetX] = max(dfs(v, check, nextY, nextX) + 1
, dp[targetY][targetX]);
}
check[targetY][targetX] = false;
return dp[targetY][targetX];
}
int main(void)
{
cin >> n >> m;
vector<vector<char>>v(n, vector<char>(m));
vector<vector<bool>>check(n, vector<bool>(m, false));
for (int i = 0; i < n; ++i)
{
string ss;
cin >> ss;
for (int j = 0; j < m; ++j)
{
v[i][j] = ss[j];
}
}
memset(dp, -1, sizeof(dp));
//for (int i = 0; i < n; ++i)
//{
// for (int j = 0; j < m; ++j)
// {
// cout << v[i][j] << " ";
// }
// cout << endl;
//}
dfs(v, check, 0, 0);
cout << dp[0][0];
}
✨정말 중요함!
어떤 알고리즘으로 접근할지에 대해
- 결론
: dfs와 dp를 사용해야 함.
dp 사용안하면, 시간 초과 발생함. - 시간초과가 발생하는 이유
: 이렇게 생각해볼 수 있음.
느낀점.
1번)
이미 방문 완료 되었는데, 다른 지점에서 돌고 돌아서 우회해서
해당 지점에 다시 도착할 경우, 시간 복잡도가 증가하는 문제가 발생함.
-> 이미 방문 완료된 위치에 대해서는 다시 방문할 필요가 없어야 함.
2번) 이러한 생각에 도달했으면, 메모이제이션을 사용해야 겠다라는
생각을 해야 하고, 내가 두번째로 만든 dfs프로세스를 엎어서 다시 작성해야함.
-> 현재 아래의 프로세스는 최대값만 설정시키고 있음.
3) 시간 복잡도는 생각해보면 , 최악의 경우, 50 * 50 * 4 임. ->1만번임.
이걸 최악으로 하면 dfs 재귀가 1만번 수행된다는 것인데,
dfs로 들어가는 비용을 줄여야 , 효율을 증대할 수 있다는 결론에 도달함.
내가 이미 방문한 노드를 재귀 들어가지 않는다면, 얼마나 효율적일 것인가!
- bfs를 사용할때는 동일한 가중치를 이용할 때만 사용해야 함.
여기서는 가중치가 원소의 값이므로, 처리할 수 없는 문제임
-
문제에서는 동전을 최대한 사용하는 문제임.
: 내가 작성한 코드는 동일한 인덱스 <-> 다른 인덱스 간의
왔다리 갔다리에 대한 처리를 한것이지만, -
정말 자세히 생각을 해보면, 해당 방문 기록에 대해,
전혀 다른 인덱스가 접근 시 , 내가 생각한 시나리오가 망치게 된다는 것임.
즉, bfs로 풀면 안되는 문제임.
어떻게 풀 것인가 에 대해서
1) 백트래킹 방식으로 접근해야 함.
2) 하나의 인덱스로 최대한 돌린 후에, 다른 인덱스로 끝까지 돌리면서
동전을 최대한 사용할 수 있게 만들어야 함.
불체크 변수 를 앞뒤로 true , 재귀 ,false 를 진행함으로써
다른 인덱스도 진행할 수 있게 만듦.
- 최대값을 증가하는 부분으로 했을 때
백트래킹 풀이 . 문제점
: 시간 초과 발생함.
왜냐하면 , 종료문을 추가적으로 추가해야 함.
반례 있음.
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
// 상하좌우
int dy[]{ -1,1,0,0 };
int dx[]{ 0,0,-1,1 };
int n, m;
int res = -1;
// 상하 좌우에서 밸류값을 곱한다음에 이동시키기
void dfs(vector<vector<char>>&v ,int Y , int X , int cnt
,vector<vector<bool>>&check)
{
if (Y < 0 || Y >= n || X < 0 || X >= m)
return;
if (v[Y][X] == 'H')
return;
// 조건문 필요
// 하여튼 이동을 못하게 될 경우에
// 무한대 처리를 해야 함.
// 방문기록이 필요함.
// 또 동일한 기록이 들어오 면 끝인데
// 처음 타겟으로부터 처리를 해야하므로.
// 백트래킹 방식으로 해야 함.
if (check[Y][X] == true)
{
cout << "-1" << endl;
exit(0);
// 재귀이기 때문에 ,, 그냥 곧바로 프로그램 끝내야 함.
//return false;
}
res = max(res, cnt);
check[Y][X] = true;
for (int i = 0; i < 4; ++i)
{
// char 형이라는 것을 인지하고 있어야 함.
int value = v[Y][X] - '0';
int nextY = Y + dy[i] * value;
int nextX = X + dx[i] * value;
if (nextY < 0 || nextY >= n ||
nextX < 0 || nextX >= m)
continue;
//cout << nextY << " " << nextX << endl;
dfs(v, nextY, nextX , cnt + 1 , check);
//res = max(res, cnt);
}
check[Y][X] = false;
//return true;
}
// 1103번. 게임.
// 16:29 ~ 55
// ~ 17:14
int main(void)
{
// 맨왼위부터 시작함.
cin >> n >> m;
vector<vector<char>>v(n, vector<char>(m));
vector<vector<bool>>check(n, vector<bool>(m));
for (int i = 0; i < n; ++i)
{
string s;
cin >> s;
for (int j = 0; j < m; ++j)
{
v[i][j] = s[j];
}
}
// 모든 노드에서 간선으로의 동일한 가중치가 아니므로
// bfs가 아님. 백트래킹으로 가야함.
//for (int i = 0; i < n; ++i)
//{
// for (int j = 0; j < m; ++j)
// {
// cout << v[i][j] << " ";
// }
// cout << endl;
//}
dfs(v, 0, 0, 1, check);
cout << res << endl;
}첫번째 풀이
-
입력 예제는 모두 맞았지만, 틀림..
-
반례
: 내용현재 인덱스에서 다음 인덱스 체크를 했음.
다른 인덱스에서 다음 인덱스로 향할 수가 있는 구조임.
-> bfs로 작성을 하게 되면, 4개의 가중치를 통해서 만드는
방식으이므로 이때는 잘못된 상황이다.
관련된 반례
https://www.acmicpc.net/board/view/28226
https://www.acmicpc.net/board/view/4882
- 설명 :
3 -> 4 -> 3 -> 2 , 4 -> 2는 9를 체크해버림. // 4에서 9를 큐에 넣을 수 있고, 체킹 확인할 경우에, 문제가 발생하는 반례임.
- 코드
#include <algorithm>
#include <string>
#include <vector>
using namespace std;
#include <iostream>
#include <stack>
#include <queue>
//상하좌우
//int dy[]{ -1,1,0,0 };
//int dx[]{ 0,0,-1,1 };
int n, m;
int bfs(vector<vector<char>>&v , vector<vector<bool>>&visited)
{
//항상 시작값은 0,0
int res = -1; // 최종 카운팅 값 .
queue<pair<pair<int, int>, int>>q;
q.push(make_pair(make_pair(0, 0), 1));
while (!q.empty())
{
int curY = q.front().first.first;
int curX = q.front().first.second;
int curCnt = q.front().second;
q.pop();
//무한번 반복됨.
if (visited[curY][curX] == true)
{
cout << -1;
exit(0);
}
visited[curY][curX] = true;
if (v[curY][curX] == 'H')
{
continue;
}
// 카운팅 처리를 해야 함.
res = max(res, curCnt);
// char형이므로, int 로 형변환을 해야 함.
int value = v[curY][curX] - '0';
//상하좌우를 새롭게 만들어야 함.
int ddy[]{ -value, value, 0 , 0 };
int ddx[]{ 0,0,-value, value };
for (int i = 0; i < 4; ++i)
{
int nextY = curY + ddy[i];
int nextX = curX + ddx[i];
//일단 테두리 체크
if (nextY < 0 || nextY >= n
|| nextX < 0 || nextX >= m)
{
continue;
}
// 원소의 값을 확인해서 큐에 넣을지 안넣을지를 처리해야 함.
// 다음 칸이 h일 경우에는 넣으면 안됨.
if (v[nextY][nextX] == 'H')
continue;
q.push(make_pair(make_pair(nextY, nextX) , curCnt + 1));
}
}
return res;
}
// 16: 40 ~ 17:27
int main()
{
//일단 bfs
// 그리고 체크 변수 필요 없음
// 동적을 무한 번 움직일 수 있음.
// 그러다가 인접한 상하좌우 이동을 못한다거나.
// 보드의 바깥으로 나가면 종료
// 이동을 못하는데, h가 발견되면 종료하도록
// 무한 번을 어떻게 처리할 것인가에 대해서
// 돌아왓던 곳을 다시 한번 방문 할경우 -> 이를 -1로 출력하자.
// 일단 한번 카운팅을 함. -> 예제 입력 5번.
// 그 다음에 안 맞으면 종료
cin >> n >> m;
vector<vector<char>>v(n, vector<char>(m));
vector<vector<bool>>visited(n, vector<bool>(m));
for (int i = 0; i < n; ++i)
{
string s;
cin >> s;
for (int j = 0; j < m; ++j)
{
v[i][j] = s[j];
}
}
//cout << "output" << endl;
//
//for (int i = 0; i < n; ++i)
//{
// for (int j = 0; j < m; ++j)
// {
// cout << v[i][j] << " ";
// }
// cout << endl;
//}
cout << bfs(v, visited);
}