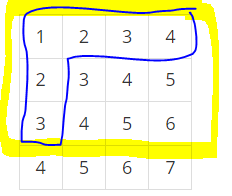
문제 유형 : 2차원 누적합 구하기
- 알고리즘 문제 해결 전략 책에도 내용 있음.
문제 분석

-
1번)
-> 문제를 분석하면 n n 의 표를 만들어서 각 지점 x1, y1 ~ x2 , y2 까지의 영역의 합을 구하는 것인데,
최악의 경우를 생각하면 x1 = 1 , y1 = 2 / x2 = n , y2 = n 일 경우임
이러한 경우에 2차원 이기 때문에 n n 의 비용 발생
-> 즉 여기서 1024 * 1024 -> 100만 -
2번) 그리고 문제에서 m번 만큼을 반복하고 싶어함.
-> 즉, 10만임. -
결과) 1번과 2번에 의해 100만 * 10만 이기 때문에
-> 100 0000 10 10000 인데 이렇게 하게 되면, 시간 제한 1초, 1억을 초과함.
-> 보통 방식의 풀이로 접근하면 시간 초과 발생함. -
결론
: m번 반복은 어쩔수 없는 상황이고, 좌표가 주어질때마다 발생하는 n * n의 비용을 없애자.
-> 누적합으로 psum 2차원 벡터를 만들어 놓고, m번 반복해서 사각형 영역의 합을 구하자!!
psum 만들기
-
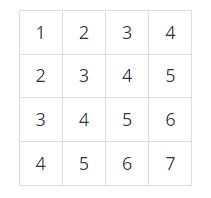
일반 arr : 0번 인덱스부터 시작.
-
psum을 만들 때, 일반적으로 [1] 번 인덱스부터 만들게 됨.
: 일차원 psum은 psum[i] = psum[i - 1] + arr[i];
이런식으로 만들 수 있음.
2차원 psum을 어떻게 만들까?
-
2차원 psum의 경우 만약에 2,2 좌표를 기준으로 한다면?
: 1열의 1,2 + 1열의 1,2 + arr[2][2] - psum[2 - 1][2 -1] 로 표현할 수 있고,
여기서의
-> 1열의 1,2 는 바로 psum[2][1] 이고
-> 1행읠 1,2 는 바로 psum[1][2] 이다. -
결론
psum[i][j] = psum[i - 1][j] + psum[i][ j - 1] + arr[i][j] - psum[i - 1][j - 1];
-
하여튼 위의 arr 표를 psum으로 만들게 되면, 이렇게 표현할 수 있음.
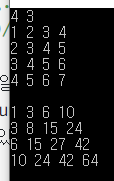
psum 점화식 코드

y1 , x1 ~ y2 , x2 좌표 범위의 합 구하기
-
생각해보기
: 저 범위를 구하고자 한다면,

-
1번
: 여기 전체 범위에서
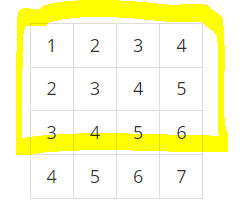
-
2번.
: 위의 작은 사각형 빼주고.

-
3번.
: 작은 사각형 빼주고

-
4번
: 2번과 3번에 의해 중복되는 사각형을 더하자.

-
5번.
: 1번 - 2번 - 3번 + 4번을 하게되면 ,
아래의 사각형 범위를 구할 수 있음!

주의할 점
: 처음에 2번과 3번 사각형 영역을 구할 때 y2- y1 이런식으로 범위를 구했는데 이게 아님
이 때는 큰 사각형을 제외한 작은 범위인 y1, x1 범위에서 생각해야 함!
왜냐 하면 저 빨간색 영역에 영향을 끼치는 구간은 3번 좌표인 y1, x1 에서 -1만큼씩
빼준 좌표를 기준으로 해서 6번 좌표 까지 진행하면 됨!
점화식

소스코드
#include <iostream>
using namespace std;
#include <string>
#include <vector>
#include <limits.h>
#include <algorithm>
#include <map>
#include <future>
#include <thread>
#include <numeric>
#include <stack>
#include <queue>
#include <memory>
#include <set>
#include <string>
#include <stack>
#include <mutex>
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
// 3 3 - 1 + 3
// 8
// 1024 * 1024 * 10만
// 1000 1000 10 10000
// -> 1억 초과
// psum 구간합을 만들어서 m번만 진행하자.
int n, m;
cin >> n >> m;
vector<vector<int>> v(n, vector<int>(n, 0));
vector<vector<int>> psum(n + 1, vector<int>(n + 1, 0));
// psum[y][x] = psum[y - 1][x] + psum[y][x - 1]
// + arr[y][x] - psum[y - 1][x - 1]
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < n; ++j)
{
cin >> v[i][j];
psum[i + 1][j + 1] = psum[i][j + 1] +
psum[i + 1][j] - psum[i][j] + v[i][j];
}
}
//cout << endl;
// psum 출력문. : 확인용.
//for (int i = 1; i <= n; ++i)
//{
// for (int j = 1; j <= n; ++j)
// {
// cout << psum[i][j] << " ";
// }
// cout << endl;
//}
// p[y1][x1] ~ p[y2][x2]
// psum[y2][x2] - psum[y2 - y1][x2]
// - psum[y2][x2 - x1] + psum[y1][x1]
int x1, y1, x2, y2;
for (int i = 0; i < m; ++i)
{
// 2 2 3 4
cin >> y1 >> x1 >> y2 >> x2;
cout << psum[y2][x2] - psum[y1 - 1][x2]
- psum[y2][x1 -1] + psum[y1 - 1][x1 - 1];
//cout << psum[y2][x2] << endl;
//cout << psum[y2 - y1][x2] << endl;
//cout << psum[y2][x2 - x1 -1 ] << endl;
//cout << psum[y1 - 1][x1 - 1] << endl;
cout << "\n";
}
//psum[y2][x2] - psum[y2 - y1 - 1][x2]
//- psum[y2][x2 - x1 -1] + psum[y1 - 1][x1 - 1]
// 42 - 10 - 6 + 1
// 32 - 5
}