Check 조건을 >= 로 했는데, 이상하다 싶으면 > 로 변경하자.

• 문제를 내가 이해 못하는 아래 부분.

이해가 안가는 부분_251009

• 왜 초과를 해야 하지???
  : 이상이어야 하지 않을까? 라는 생각을 하는데

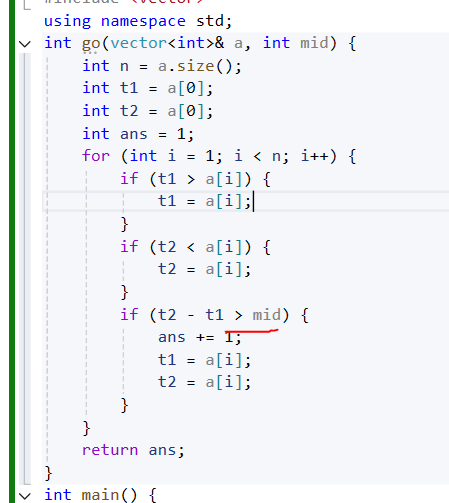
• mid값을 각 구간 중에서 최대값 - 최소값 주에서 최소값에 해당되는 내용이다.

• 잠시만 생각을 해보자. mid값이 2이고 구간에서 차이가 2가 되었는데 , 여기서 카운팅을 해야할까?

핵심.

• -> 최소값이라는 표현을 썻기 때문에 반드시 최소값보다 큰 표현을 사용해야 하기 때문에 mid값보다 큰 차이값을 갖는 구간이야 말로 조건에 만족한다.

• 구글링 내용.
  

• 그나마 도움이 된 블로그
  https://blogshine.tistory.com/151

---

문제 유형

: 이분법을 통한 구간 나누기

해결전략 : 시간복잡도.

• 생각해보기
  : m개 이하로 구간을 나눌 수 있다고 하는 거는 아래의 3개로 나누는 것뿐 아니라, 2개 1개로 구간을 정할 수 있다는 건데.

• 일단은 3개로 한번 나누어보았다.

• 앞에서부터 오름차순으로 하면 이런 경우인데.
  독특한 갯수가 나오는데

• 6개, 5개, 4개 순으로 ... 나오는데 바로 팩토리얼이다.
  그런데 아직 3개 구간만 나눈 것이고,
  

• 2개 구간으로 나누면 이렇게 되겠지?
  

결론

: 8개 중에서 3개이하의 구간으로 했는데도
6! + 7 + 1 개 이므로 즉 (n-1) 팩토리얼이 나온다.

• 그런데 n자체가 정말 크므로 단 한번의 최악의 예제에서는 불가하므로, 위의 방법으로 하면 안된다.

---

어떻게 접근할까?

• 일단은 백준 파일의 내용은 이렇다.
  => 최대값의 최소값을 구하는 문제는 이분탐색을 사용한다...

이분탐색

: 지금까지 풀었던 이분탐색 문제의 특징은 나도 몰랐지만, 최소값, 최대값을 구하는 문제 였다.

• 아래 문제들을 보아라.
  https://www.acmicpc.net/workbook/view/24424

지금의 문제를 보자.

• 여기서도 어쨋든 최대값을 구하라 문제이다.
  

• 나는 솔직히 그간 풀어왔던 이분탐색 풀어야 겠다. 결정내린 것은 범위가 굉장히 컸기 때문이었다.

• 문제에서는 m개 이하라고 했으므로
  m이 초과되는 순간을 false로 해서 이분탐색을 진행하면 된다.
  

어떻게 풀까?

• 나만의 이분법 공식
  : diff값을 특정값으로 결정하고, 문제에서 나온대로 각 구간의 최대값과 최소값의 diff 값과의 비교를 하면서 카운팅을 하자.

• 중요한 것은 여기에 현혹되면 안된다.
  : 어떻게 최대값 6이 나왔는지..

• 6은 아래의 경우와는 다르지만 1개의 구간에서 찾을 수 있으므로 아래처럼 3개의 구간은 아니지만 가능하다.
  

주의할점

• 구간을 어떻게 나눌것인가가 중요하다.