개념

: 문제에서 중복되는 수는 제거하고 있다. 즉 조합이다.

• 조합을 생각하면, 재귀도 있지만, dp도 생각해내야 한다.

• 문제를 읽어보면, 재귀로는 굉장히 복잡할듯 하다.
  그래서 dp로 접근하자.

접근하기 1

• 일단 중복 처리를 제외하고, 숫자 i를 만드는 점화식은 이거다.
  

-> 이어서 쉬운 계단수와 유사하게 접근하면 된다.

접근하기 2

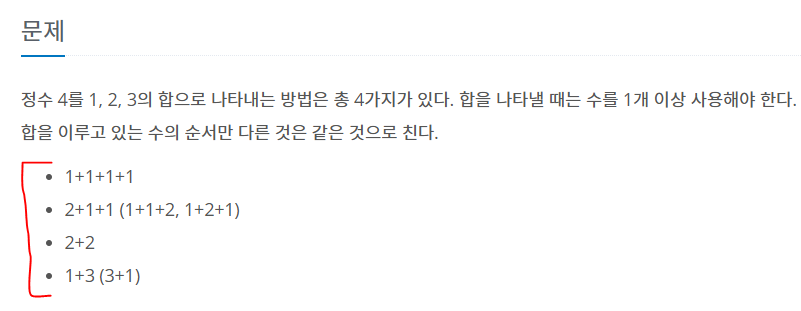
• 주어진 예시이다.
  

• 그리고 어떤 수 i를 만다는데 1,2,3을 항상 1개씩을 사용해야 한다고 한다.

• dp로 접근하기로 했으니 점화식을 작성해야 하는데,,, 흠..
  -> 일단 어떤 수 i는 정해졌다. dp[i] 그리고,
  -> 1,2,3 중에서 1개를 사용해야 한다고 하므로,
  2차원 형태의 점화식으로 새로운 정보를 넣어주면 어떨까? 를 생각해야 한다.

• 일단 아래의 경우 dp[i][?] : i는 4이고,
  물음표에는 어떠한 정책을 작성할까? 를 생각해보자.
  : 일단은 물음표에는 1과 2와 3이 들어가야 한다.
  

• 정수 4를 숫자 1을 가지고 만드는 경우는 3인가?

• 정수 4를 숫자 2로 만드는 경우는 2인가?

• 정수 4를 숫자 3으로 만드느 경우는 1인가?
  => 그러면 정답은 6이어야 하는데, 답은 4이다.

: 잘못된.

접근하기 3

• 최대한 정답 cnt : 4에 근사하게 생각해보자.

• 1) 숫자 4를 만드는데 1 이하로 사용되는 거는 1+1+1+1
  -> 1개다.

• 2) 숫자 4를 만드는데 2 이하로 만드는 경우는
  -> 2+1+1 / 2 + 2 => 2개다.

• 3) 숫자 4를 만드는데 3 이하로 만드는 경우는
  -> 1+3 => 1개다.

=> 오오옷!!! 정말인가?
여기서 나온 점화식은 i번 숫자를 만드는데 j숫자 이하의 조합으로 만드는 경우의 수의 합이라고 할 수 있따.

-> 이 생각을 다른 n에 대입해보면, 맞다.

알아야 할점

• 그렇다고 한다...
  

• ㅇㅇ
  

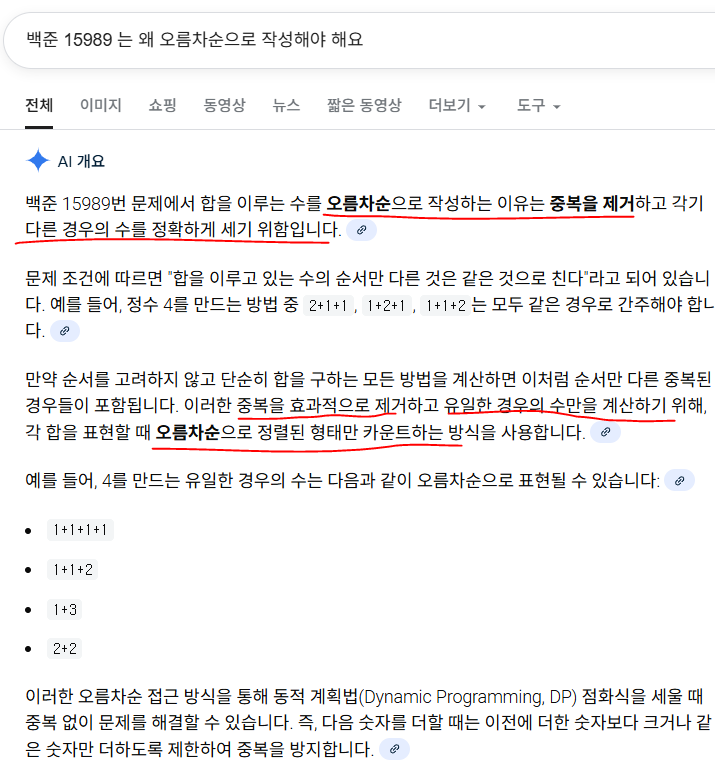
점화식

• 접근하기 1과 접근하기 3을 합하자.