생각해볼 점이 많은 구현 문제

벡터 어떻게 초기화

• 일단 배열 구성할때 보통 v[y][x] 로 표현했는데, 문제에서
  여기서 r 과 c가 나오는데
  보통 r는 가로 c는 세로 라서 음 뒤집어야 하나 생각이 들지만,

• 저기 아래를 읽어보면 r을 y로 판단하고, c를 x로 판단해서 진행하기로 결정함.

중복되는 나무 처리.

• 문제를 읽어보면,

가) 누적되는 양분 벡터
나) 갱신해주는 변하지 않는 양분 벡터
다) [r][c] 지점에 중복될 수 있는 나무들이다.

-> 이렇게 메모리가 필요하다.

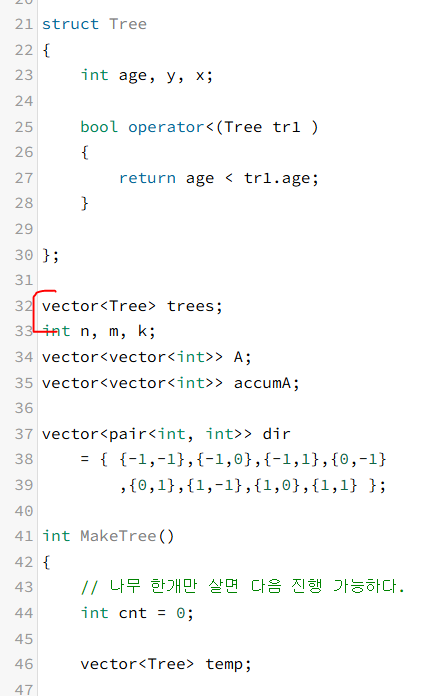
다번) 중복되는 나무들에 대한 나의 첫번재 생각은 이렇게 구조체로 만든 후 vector로 가지고 접근했는데, 이렇게 하게 되면,
erase를 해야 하거나, 조건처리로 if(age == 0) 를 해야 한다.

• 그리고 sort를 위해서 operator 함수도 필요하다.
  

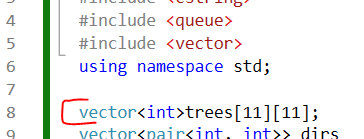
• 이렇게 해보자.
  나무들을 2차원 벡터 형태로 가지고 있짜.
  

• 그리고 push_back 하는 방법
  

• sort 할 때 그냥 모든 trees[][] 순회하면 가장 작은 친구부터 처리될 것이다.

봄에 대해서 : true인 경우

• 봄, 여름, 가을, 겨울에 대한 코드를 작성해야 하므로
  코드가 번잡해질 것으로 예상된다...
  -> 아예 하나의 시즌이 시작된다는 주석을 작성하고 시작하자.

• 봄부터 시작해보자.
  : 봄의 경우 [i][j] 에 있는 나무들 중에서 accum양분과의 비교를 한다.
  accum양분보다 작다면 해당 [i][j] 에 있는 나무는 죽는다.
  그렇지 않다면 해당 나무는 1살 증가한다.

• 양분보다 작다는 구간의 코드는 여기다.
  

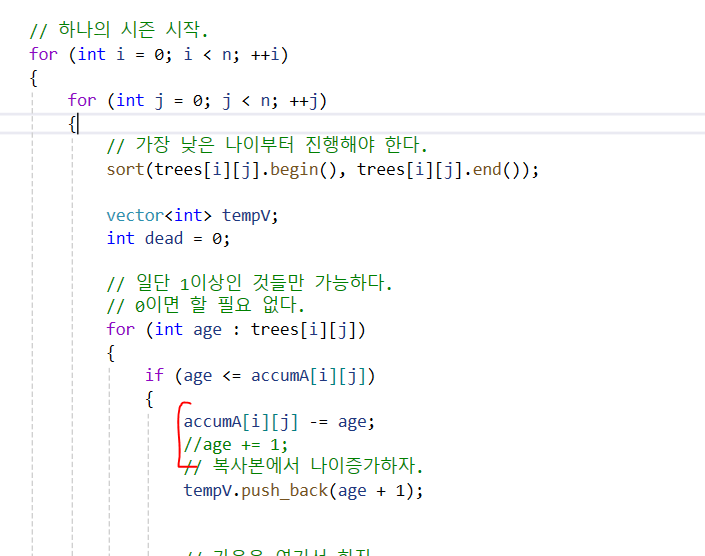
• 생각해볼 점이 있다.
  양분이 없다면 해당 나무는 죽게되는데, 그렇다면 trees[i][j]에서 erase를 해야 한다.

-> erase를 하지말고, 어차피 우리가 하는 동작은
[i][j] 지점에 있는 나무들로 하고 있다. age가 0인 친구들은
다음 시즌에 확인할 필요조차 없다.
그래서 temp변수를 사용하자.

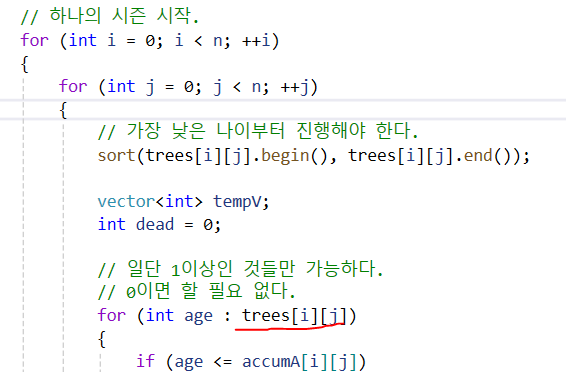
• temp사용
  

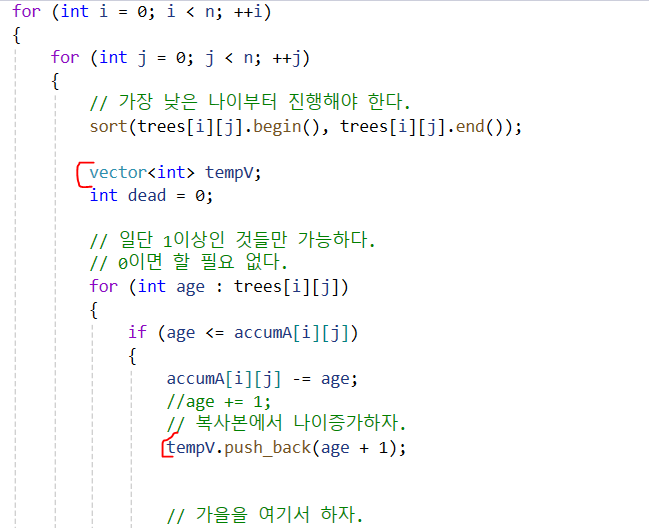
• [i][j] 에 있는 모든 나무들 완료 후에 다음 시즌을 위해서 여기서 갱신한다.
  

• 양분값보다 작다면 굳이 temp에는 넣을 필요가 없다.

봄에 대해서 false 인 경우

• 이부분인데, 처음에는 이렇게 바로 집어넣었는데, 8번 입력예제에서 틀린다... 아마 나는 91만 나올것이다. 정답은 85.
  

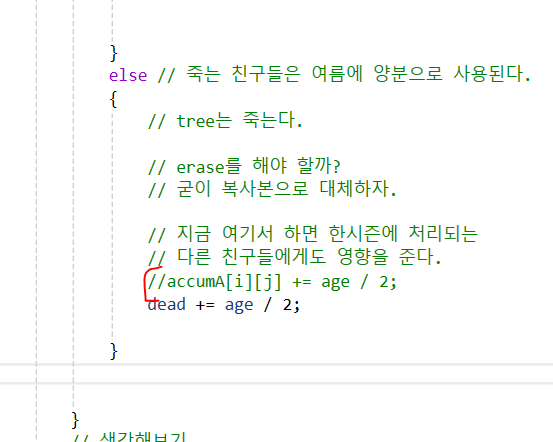
• 왜 그럴까? 여기는 코드를 통해서 생각해봐야 하는 부분이다.
  : 한 시즌의 여름 진행시 모든 [i][j] 에 있는 나무들에 관해서
  완료 한 후에 해야되는 작업이다.
  완료 되지 않고 하게 되면 뒤이어서 나오는 나무들도 기존의 양분을 가지고 처리해야 하는데, 위의 코드로 하게 되면 어라 내 앞에 친구가 죽어서 양분이 추가되어 버렸네? 양분이 넉넉하다!
  나이스! 나는 다음시즌에도 진행된다. 라는 시나리오가 발생한다.
  

• 그래서 이렇게 temp변수인 dead로 진행함.
  모든 trees[i][j] 에 있는 원소가 완료 후에 처리하자.
  // 참고로 아직 하나의 시즌은 끝나지 않았다.
  // 그냥 trees[i][j] 에 있는 모든 원소가 끝나는 지점일뿐.

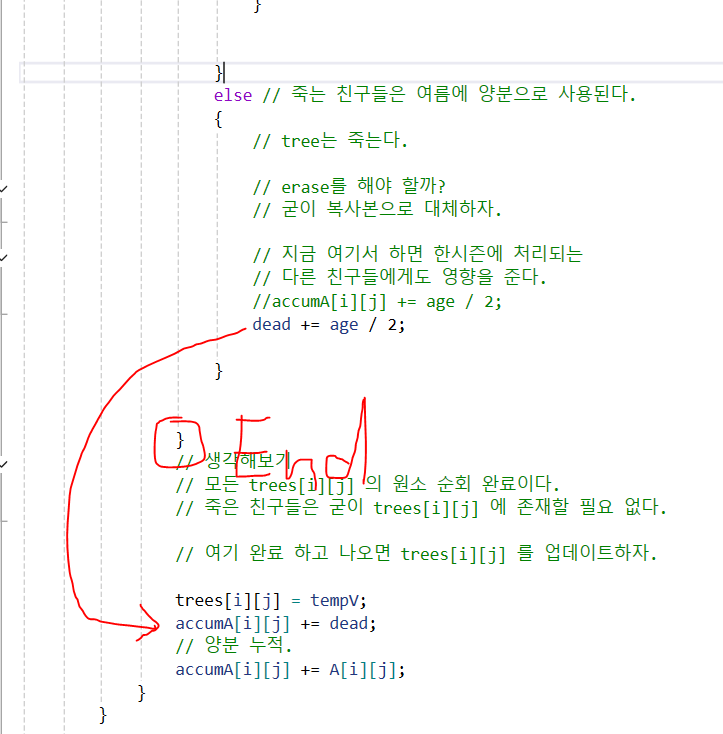
가을에 대해서...

• 가을은 살아있는 나무에 관해서 진행하는 것이므로 봄의 코드에서 봄 처리후에 하면 된다.
  

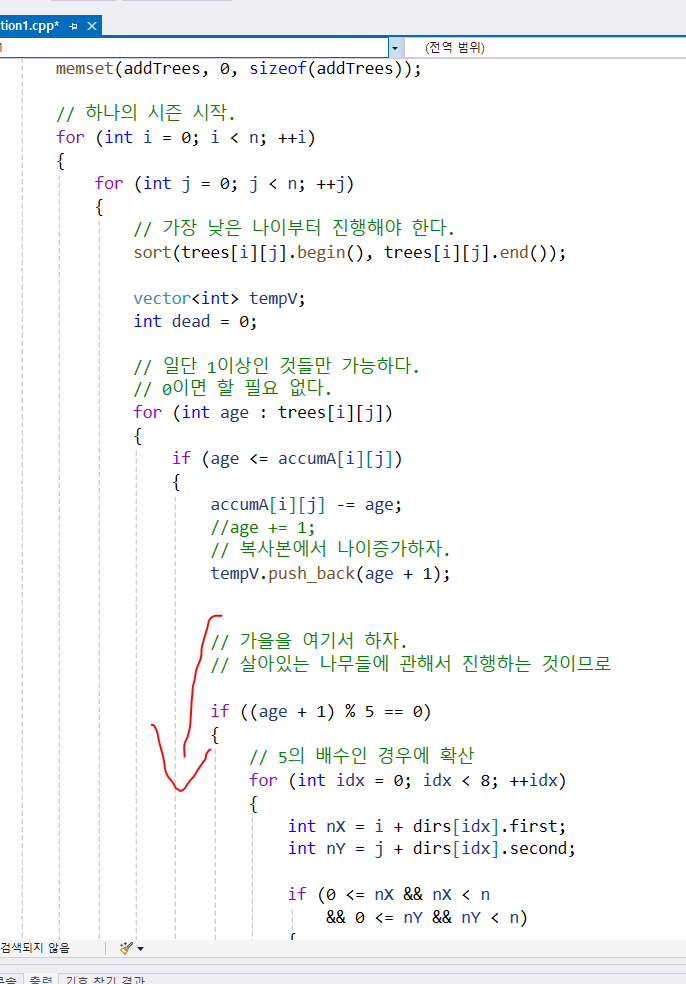
• 핵심은 여기다. 여기도 봄의 false인 부분과 마찬가지고 한 시즌이 완료 된 후에야 확산되는 나무를 추가해야 한다!
  그래서 temp 변수에다가 넣어놓고,
  

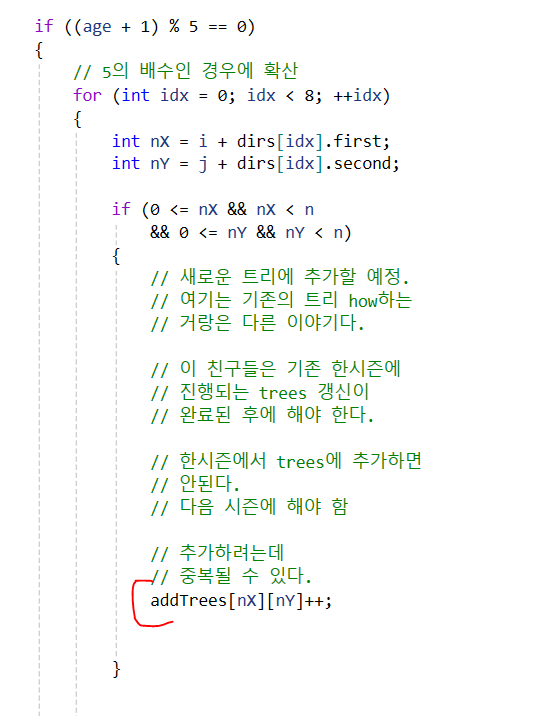
• 여기서는 하나의 시즌이 완료된 후에야 새로운 나무를 추가해야 한다.
  

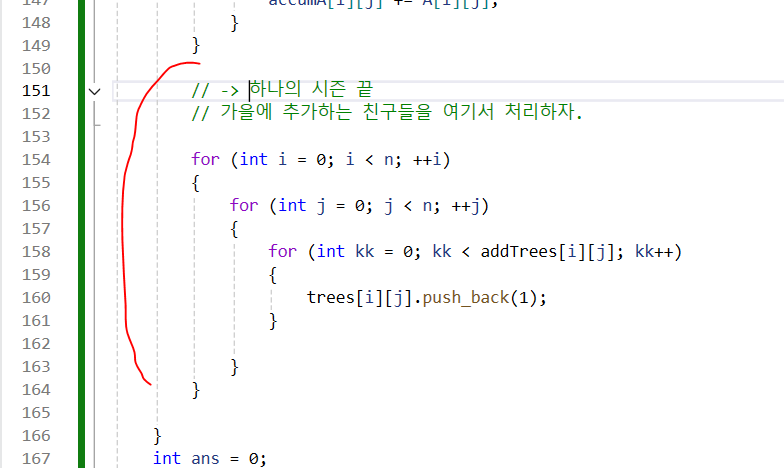
결론

: 삼성 문제이고, 정답률이 22퍼인 이유가 있다.

• 코테에서 유사한 문제가 나왔을 때

1. 멘붕하지 말자.
2. 주석을 작성하면서 어떠한 의미인지를 명시하자.
3. 차라리 몇개의 입력 예제에서 틀린다고 한다면 감사하게 생각하고, 내가 작성한 코드의 의미와 문제의 내용을 다시 한번 비교하면서 검토해보자.