문제 해결전략

: 여러 개의 시작점을 갖는 다익스트라.
// 아래의 내용을 읽어보면, 즉 불특정 면접장이고, dist 테이블에는 뭘해도 좋으니 가장 최단거리임을 알수 있다.

왜 틀렸을까???

• 기존의 다익스트라와는 다르게 모든 도시 번호 중에서
  여러개의 면접장 중에서 최단거리를 출력하는 문제이다.
  -> 그래서 그냥 다익스트라 처럼 하면 되겠지? 라는 안일한 생각을 함.

-> 그래서 어떻게 했냐면?
: 모든 정점을 시작정점으로 해서 다른 정점에 대해 다익스트라를 구함.
그리고 dist[면접장 번호] 여러개 중 가장 작은 값에서 면접장 번호와 dist를 저장함.

• 그런데 이게 끝이 아니라, 모든 면접장에 대해 진행해야 한다.
  => 일단 코드가 굉장히 번잡해질 것으로 생각됨.

시간복잡도는 생각해보면,
ELog(n) x 면접장 수 이므로
: 50만 x log(10만) x 10만이므로,
=> 50만 x 100(최소) x 10만이다....
==> 50 0000 00 0 0000 : 나의 생각이 맞더라도 시간복잡도 초과다.

다른 접근법이 필요하다.

• 기존의 다익스트라는 하나의 시작점으로 해서 모든 정점의
  최단거리 distTable을 구하는 것이므로,

a -> b : cost 를 그대로 vertex[a].push_back({b, cost});
로 표현했지만,

• 지금은 여러개의 면접장 중 최단 dist에 있는 거를 택해라 문제이므로 문제를 바라보는 거는 반대로 뒤집자.

• 기존에는 도시(a)에서 다른 도시(b)로 가는 cost 중 면접장은 b번이다. 면접장은 b번에 해당한다.

• 기준을 도시가 아닌 면접장 입장에서 바라보는 것이 타당하다.
  왜냐하면 문제에서 면접장 여러개 중에서 가장 가까운 거를 선택해! 라고 했기 때문에

-> 그리고 이렇게 하면 위의 시간복잡도도 자연스럽게 해결된다.
: 왜냐하면 시작정점인 면접장을 모두 pq에 넣은 상태에서 모든
정점으로의 distTable을 구하는 것이므로 ELog(n) 의 시간 복잡도로 처리하게 된다.

dist 초기치에 대해서

: 다익스트라의 dist의 최대값은 항상 1e9로 사용했는데,

• 최악의 간선 즉 1번에서 2번 3번 ~ n번까지
  연결되어 있따고 한다면,

-> 10만 x 50만 x 10만 이므로
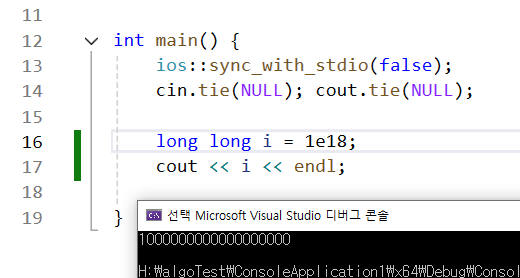
10 0000 50 0000 10 0000 => 5000000000000000 이다.
(0이 15개다. 5는 1개 )
int 타입과 1e9로는 불가하다.
-> long long타입과 1e18로 가야 한다.