2776번. 암기왕_이분탐색

이분탐색 시 주의할 점.

• right = v.size() 로 하기에는 적절치 못함.

  v: 0 1 2 3 4 5 가 있고, 5번째 인덱스에 위치할 때 찾을 수 있다고 한다면
  이 때의 사이즈는 6임. 그러면 v[6] 으로 접근하면 range 오류 발생함.
  따라서 right 설정할 때 v.size() - 1로 설정하자.

• right와 left 갱신에 대해

  이런식으로 right 와 left 를 갱신할 경우, 무한 루프임.
  왜냐하면 끝의 인덱스인 0과 size() - 1 에 위치할 경우, 계속 mid 값만 유지하려고 하기 때문에 접근을 못함.
  
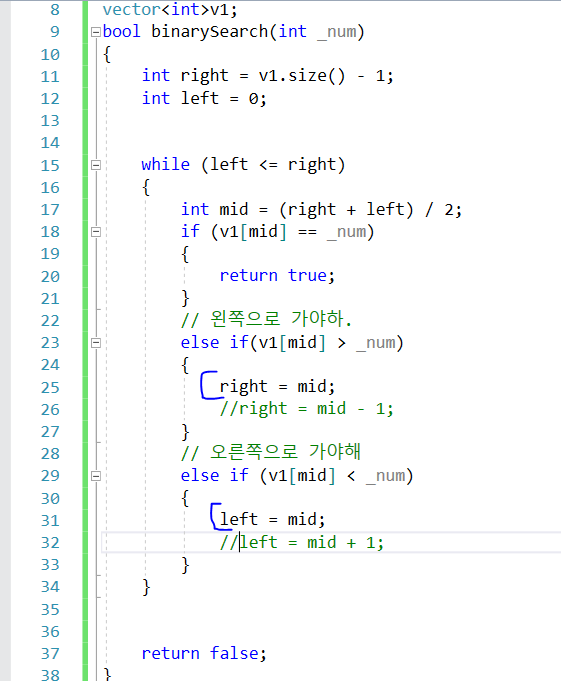
  예 를 들어
  인덱스 0 1 2 3 4 5
  값 0 1 8 9 10 11 이라고 할 때, 11을 찾기 위해서는 5까지 진행해야 함.
  left = mid 로 진행할 경우 , mid -> 2(0 + 5) -> 3(2 + 5)
  -> 4(3 + 5) -> 4(4 + 5) -> 4(4 + 5) -> ....
  마지막에서 도저히 끝이 안남.
  이로 인해서 이런식으로 바이너리 서치해야 함.

---

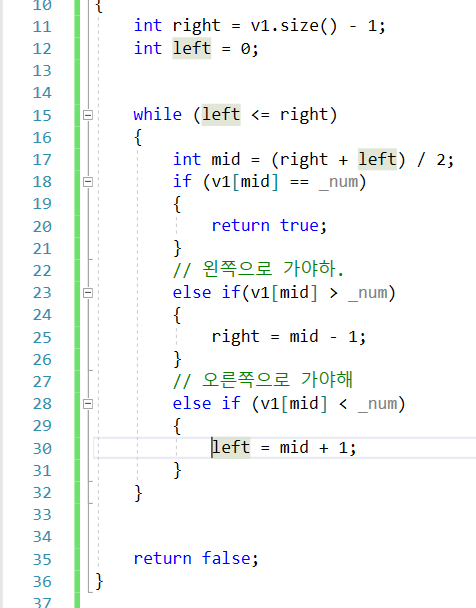
기록

• 220820

문제점.

1) 걸림돌 1번

cin vs scanf..
-> 백준에서는 scanf를 사용하자.
-> cin으로 하면 틀림.
참고 사이트
https://ansohxxn.github.io/cpp/iospeed/

2) 걸림돌 2번 : 이분 탐색 주의할점.

이분 탐색에서 end값 지정할 때 v.size() - 1로 초기값 맞추고 진행하자.
타겟값이 마지막 원소보다 작아서, 계속 인덱스가 증가함.
이렇게 되면 , mid 인덱스값이 v.size()값이 될텐데,
v.size()라는 인덱스는 존재하지 않음.

이유 : 1 , 2 , 3 , 4 ,5 vs 7을 비교한다고 했을때
mid 값 은 7보다 작으므로 인덱스가 증가하게 되면서 마지막 원소와 비교를
해야하는데, v.size()라는 인덱스는 존재하지 않으므로, 런타임 에러 발생함.

3) 테스트 케이스 입력

: 이부분 놓침..

코드

#include <iostream>
#include <vector>
using namespace std;
#include <algorithm>

bool binarySearch(vector<int>&v1, int target)
{
	// 0 1 2 3 4 
	// 1 2 3 4 5 
	// 1 찾기 
	// 3 찾기 
	// 7 찾기
	// 5찾기 
	// 9 찾기 
	int start = 0;
	int end = v1.size() - 1;
	int mid;
	// 0 4 , 2 // 3 4 , 3 / 4 4 , 4
	while (start <= end)
	{		
		mid = (start + end) / 2;
		if (v1[mid] < target)
		{
			start = mid + 1;
		}
		else if (v1[mid] == target)
		{
			return true;
		}
		//
		else if (v1[mid] > target)
		{
			end = mid - 1;
		}

	}

	return false;
}

int main() 
{
	// n : 100만.
	// m : 100만. 
	// => 100 만 * 100만.. 
	// => 엄청나게 많은 수이므로 
	// logN의 비용을 나타내는 이분탐색으로 가자.
	// 그냥 유무가 알면됨.
	int t;
	cin >> t;

	for (int k = 0; k < t; ++k)
	{
		int n, m;

		scanf("%d", &n);
		//cin >> n;
		vector<int>v1(n);

		for (int i = 0; i < n; ++i)
		{
			scanf("%d", &v1[i]);

			//cin >> v1[i];
		}
		scanf("%d", &m);

		//cin >> m;
		

		sort(v1.begin(), v1.end());
		int x;
		for (int i = 0; i < m; ++i)
		{
			scanf("%d", &x);

			//cin >> x;
			if (binarySearch(v1, x))
			{
				cout << 1 <<"\n";
			}
			else cout << 0 << "\n";
		}
	}
	

}